Detské ihrisko 2
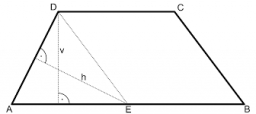
Detské ihrisko má tvar lichobežníka, ktorého rovnobežné strany majú dĺžku 36 m a 21 m, zvyšné dve strany dĺžku 14 m a 16 m. Určte veľkosť vnútorných uhlov lichobežníka.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- vyjadrenie neznámej zo vzorca
- planimetria
- pravouhlý trojuholník
- trojuholník
- lichobežník
- kosínusová veta
- sínusová veta
- rovnobežník
- goniometria a trigonometria
- sínus
- kosínus
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Určte 21
 Určte vzdialenosť dvoch neprístupných miest K, L, ak sa z bodov A, B, ktoré sú od seba vzdialené 870 m, namerali veľkosti uhlov KAL=62°10", LAB= 41°23", KBL=66°34", LBA= 34°52". Ďakujem.
Určte vzdialenosť dvoch neprístupných miest K, L, ak sa z bodov A, B, ktoré sú od seba vzdialené 870 m, namerali veľkosti uhlov KAL=62°10", LAB= 41°23", KBL=66°34", LBA= 34°52". Ďakujem. - Delostrelectvo 2
 Cieľ C pozorujú z dvoch delostreleckých pozorovateľní A, B navzájom vzdialených 296 m. Pritom uhol BAC = 52°42" a uhol ABC = 44°56". Vypočítajte vzdialenosť cieľa od pozorovateľne A.
Cieľ C pozorujú z dvoch delostreleckých pozorovateľní A, B navzájom vzdialených 296 m. Pritom uhol BAC = 52°42" a uhol ABC = 44°56". Vypočítajte vzdialenosť cieľa od pozorovateľne A. - V trojuholníku 18
 V trojuholníku ABC je dané b=5 cm, c=6 cm, /BAC/ = 80°. Vypočítajte veľkosti ostatných strán a uhlov, ďalej určte veľkosti ťažnice tc a obsah trojuholníka.
V trojuholníku ABC je dané b=5 cm, c=6 cm, /BAC/ = 80°. Vypočítajte veľkosti ostatných strán a uhlov, ďalej určte veľkosti ťažnice tc a obsah trojuholníka. - V trojuholníku 16
 V trojuholníku ABC poznáme a = 4 cm, b = 6 cm, γ = 60°. Vypočítajte obsah, polomer vpísanej a opísanej kružnice.
V trojuholníku ABC poznáme a = 4 cm, b = 6 cm, γ = 60°. Vypočítajte obsah, polomer vpísanej a opísanej kružnice.
- Silu veľkosti
 Silu veľkosti F = 100 N rozložte na dve kolmé zložky s veľkosť'ami F1, F2 tak, aby uhol medzi silami F1 a F bol 43°52'.
Silu veľkosti F = 100 N rozložte na dve kolmé zložky s veľkosť'ami F1, F2 tak, aby uhol medzi silami F1 a F bol 43°52'. - Vypočítajte 228
 Vypočítajte veľkosť najväčšieho uhla v trojuholníku ABC, ak a = 7 cm, b = 8 cm, c = 13 cm. Vypočítaj obsah trojuholníka, výšku na stranu a.
Vypočítajte veľkosť najväčšieho uhla v trojuholníku ABC, ak a = 7 cm, b = 8 cm, c = 13 cm. Vypočítaj obsah trojuholníka, výšku na stranu a. - Plocha 6
 Plocha na výcvik streľby má tvar lichobežníka, ktorého rovnobežné strany sú dlhé 36m, 21m, zvyšné strany majú dĺžku 14m, 16m. Určte veľkosť vnútorných uhlov pri dlhšej základni.
Plocha na výcvik streľby má tvar lichobežníka, ktorého rovnobežné strany sú dlhé 36m, 21m, zvyšné strany majú dĺžku 14m, 16m. Určte veľkosť vnútorných uhlov pri dlhšej základni. - Lietadlo 21
 Lietadlo letiace smerom k pozorovateľni, z nej bolo zamerané v priamej vzdialenosti 5300 m pod výškovým uhlom 28º a po 9 sekundách v priamej vzdialenosti 2400 m pod výškovým uhlom 50º. Vypočítajte vzdialenosť, ktorú v tomto časovom intervale lietadlo prel
Lietadlo letiace smerom k pozorovateľni, z nej bolo zamerané v priamej vzdialenosti 5300 m pod výškovým uhlom 28º a po 9 sekundách v priamej vzdialenosti 2400 m pod výškovým uhlom 50º. Vypočítajte vzdialenosť, ktorú v tomto časovom intervale lietadlo prel - Pochodový uhol
 Hliadka mala určený pochodový uhol 13°. Po prejdení 9 km sa uhol zmenil na 62°. Týmto smerom išla hliadka 10 km. zistí vzdialenosť od miesta, z ktorého hliadka vyšla. Pozn. Pochodový uhol - azimut - je uhol, ktorý zvierajú polpriamky – jedna smerujúca ku
Hliadka mala určený pochodový uhol 13°. Po prejdení 9 km sa uhol zmenil na 62°. Týmto smerom išla hliadka 10 km. zistí vzdialenosť od miesta, z ktorého hliadka vyšla. Pozn. Pochodový uhol - azimut - je uhol, ktorý zvierajú polpriamky – jedna smerujúca ku
- Vysokej 71654
 Z veže 15m vysokej a od rieky 30 m sa javila šírka rieky v uhle 15 °. Aká široká je rieka v tomto mieste?
Z veže 15m vysokej a od rieky 30 m sa javila šírka rieky v uhle 15 °. Aká široká je rieka v tomto mieste? - Určte 9
 Určte vzdialenosť dvoch neprístupných miest P, Q, ak vzdialenosť dvoch pozorovacích miest A, B je 2000m a ak poznáte veľkosť uhlov QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažované miesta A, B, P, Q ležia v jednej rovine.
Určte vzdialenosť dvoch neprístupných miest P, Q, ak vzdialenosť dvoch pozorovacích miest A, B je 2000m a ak poznáte veľkosť uhlov QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažované miesta A, B, P, Q ležia v jednej rovine. - Vzdialenosť 67754
 Adam (A) stojí na jednom brehu rieky, Bedrich (B) stojí na druhom. Aby mohla byť stanovená ich vzdialenosť, bola na jednom brehu rieky zmeraná základňa AC o dĺžke 136 m a uhly CAB s veľkosťou 70°21' a ACB s veľkosťou 43°44'. Aká je vzdialenosť Adama a Bed
Adam (A) stojí na jednom brehu rieky, Bedrich (B) stojí na druhom. Aby mohla byť stanovená ich vzdialenosť, bola na jednom brehu rieky zmeraná základňa AC o dĺžke 136 m a uhly CAB s veľkosťou 70°21' a ACB s veľkosťou 43°44'. Aká je vzdialenosť Adama a Bed - V trojuholníku 14
 V trojuholníku ABC urči veľkosť strán a a b a veľkosti vnútorných uhlov β a γ, ak je dané c = 1,86 m, tažnica na stranu c je 2,12 m a uhol alfa je 40° 12'.
V trojuholníku ABC urči veľkosť strán a a b a veľkosti vnútorných uhlov β a γ, ak je dané c = 1,86 m, tažnica na stranu c je 2,12 m a uhol alfa je 40° 12'. - Stred prepony
 Bod S je stred prepony AB pravouhlého trojuholníka ABC. Vypočítajte obsah trojuholníka ABC, ak ťažnica na preponu je dlhá 0,2 dm a ak platí |∢ACS| = 30°.
Bod S je stred prepony AB pravouhlého trojuholníka ABC. Vypočítajte obsah trojuholníka ABC, ak ťažnica na preponu je dlhá 0,2 dm a ak platí |∢ACS| = 30°.
- Delostrelectvo
 Cieľ C pozorovali z dvoch delostreleckých pozorovateľní A, B, ktoré sú od seba vzdialené 975m, pritom veľkosť uhla BAC je 63°, veľkosť ABC je 48°. Vypočítajte vzdialenosť bodov A a C.
Cieľ C pozorovali z dvoch delostreleckých pozorovateľní A, B, ktoré sú od seba vzdialené 975m, pritom veľkosť uhla BAC je 63°, veľkosť ABC je 48°. Vypočítajte vzdialenosť bodov A a C. - Kosinusova 2
 Kosinusova a sinusova veta: Vypočítajte všetky chýbajúce hodnoty z trojuholníka ABC. c = 2,9 cm; β = 28°; γ = 14°α =? °; a =? cm; b =? cm
Kosinusova a sinusova veta: Vypočítajte všetky chýbajúce hodnoty z trojuholníka ABC. c = 2,9 cm; β = 28°; γ = 14°α =? °; a =? cm; b =? cm - Kosinusova
 Kosinusova a sinusova veta : Vypočítajte všetky chýbajúce hodnoty z trojuholníka ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? °
Kosinusova a sinusova veta : Vypočítajte všetky chýbajúce hodnoty z trojuholníka ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? °
