MO Z9 2019 domáce kolo
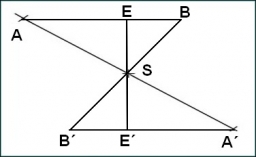
V trojuholníku ABC leží bod P v tretine úsečky AB (bližšie bodu A), bod R je v tretine úsečky PB (bližšie bodu P) a bod Q leží na úsečke BC tak, že uhly PCB a RQB sú zhodné.
Určte pomer obsahov trojuholníkov ABC a PQC.
Určte pomer obsahov trojuholníkov ABC a PQC.
Správna odpoveď:
Zobrazujem 3 komentáre:
Dr Math
no asi tazko, kedze ABC je vacsi trojuholnik ako PQC. PQC lezi v trojuholniku ABC a preto jeho obsah je mensi. preto pomer je 9:2, tj. S(ABC) :S(PQC) = 9:2
4 roky 2 Likes
Tipy na súvisiace online kalkulačky
Vyskúšajte našu kalkulačka na prepočet pomeru.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Polovica obĺžnika
 Vypočítajte obsah pravouhlého trojuholníka ABC s odvesnami a=15cm, b=1,7dm.
Vypočítajte obsah pravouhlého trojuholníka ABC s odvesnami a=15cm, b=1,7dm. - Výška, uhol a strana
 Vypočítajte obsah trojuholníka ABC, v ktorom poznáte stranu c=5 cm, uhol pri vrchole A= 70 stupňov a pomer úsekov, ktoré vytína výška na stranu c je 1:3.
Vypočítajte obsah trojuholníka ABC, v ktorom poznáte stranu c=5 cm, uhol pri vrchole A= 70 stupňov a pomer úsekov, ktoré vytína výška na stranu c je 1:3. - Rovnoramenný trojuholník -VU
 Vypočítajte dĺžky strán v rovnoramennom trojuholníku, ak je dana výška (na základňu) Vc= 8,8cm a uhol pri zakladni alfa= 38°40`.
Vypočítajte dĺžky strán v rovnoramennom trojuholníku, ak je dana výška (na základňu) Vc= 8,8cm a uhol pri zakladni alfa= 38°40`. - Tetiva - uhol
 Je daná kružnica k so stredom v bode S a polomerom 6 cm. Vypočítaj veľkosť stredového uhla, ktorý patí tetive dlhej 10 cm.
Je daná kružnica k so stredom v bode S a polomerom 6 cm. Vypočítaj veľkosť stredového uhla, ktorý patí tetive dlhej 10 cm. - Z drevenej 2
 Z drevenej plátne tvár obdĺžnika s rozmermi 80 CM a 65 CM odrezal stolár pravoúhly trojuholník s voľnými stranami 550 mm a 200 mm. kolko centimetrov štvorcových bude tvoriť odpad?
Z drevenej plátne tvár obdĺžnika s rozmermi 80 CM a 65 CM odrezal stolár pravoúhly trojuholník s voľnými stranami 550 mm a 200 mm. kolko centimetrov štvorcových bude tvoriť odpad? - Obsah 44
 Obsah pravouhlému trojuholníka ABC je 346 cm² a uhol pri vrchole A je 64°. Vypočítajte dĺžky odvesien a, b.
Obsah pravouhlému trojuholníka ABC je 346 cm² a uhol pri vrchole A je 64°. Vypočítajte dĺžky odvesien a, b. - Ťažnice v PT
 V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku.
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku. - Záhrada 41
 Záhrada má tvar pravoúhleho lichobežníka a=50m, c=30m, d=15m. Koľko metrov pletiva potrebujeme na jej oplotenie, ak musíme k vypčíitanej dĺžke pripočítať 8% stratu?
Záhrada má tvar pravoúhleho lichobežníka a=50m, c=30m, d=15m. Koľko metrov pletiva potrebujeme na jej oplotenie, ak musíme k vypčíitanej dĺžke pripočítať 8% stratu? - Rebrík 15
 Rebrík dlhý 6,5 m je opretý o zvislú stenu. Jeho spodný koniec sa opiera o zem vo vzdialenosti 1,6 m od steny. Určte, do akej výšky dosahuje horný koniec rebríka a pod akým uhlom je rebrík opretý o stenu.
Rebrík dlhý 6,5 m je opretý o zvislú stenu. Jeho spodný koniec sa opiera o zem vo vzdialenosti 1,6 m od steny. Určte, do akej výšky dosahuje horný koniec rebríka a pod akým uhlom je rebrík opretý o stenu. - Deltoid 2
 Papierový šarkan má tvar deltoidu ABCD, v ktorom sú dve kratšie strany dlhé po 30 cm, dve dlhšie strany po 51 cm a kratšia uhlopriečka má dĺžku 48 cm. Určte veľkosti vnútorných uhlov daného deltoidu.
Papierový šarkan má tvar deltoidu ABCD, v ktorom sú dve kratšie strany dlhé po 30 cm, dve dlhšie strany po 51 cm a kratšia uhlopriečka má dĺžku 48 cm. Určte veľkosti vnútorných uhlov daného deltoidu. - Kocka 65
 Kocka je zložená zo 64 malých kociek z ktorých každá má dĺžku hrany 15 mm. Vypočítaj dĺžku stenovej a telesovej uhlopriečky.
Kocka je zložená zo 64 malých kociek z ktorých každá má dĺžku hrany 15 mm. Vypočítaj dĺžku stenovej a telesovej uhlopriečky. - Výška
 Výška je nakreslená z vrcholu rovnoramenného trojuholníka, ktorý tvorí pravý uhol a dva zhodné trojuholníky. Výsledkom je, že výška rozdeľuje základňu na dva rovnaké segmenty. Dĺžka výšky je 18 palcov a dĺžka základne je 15 palcov. Nájdite obvod trojuholn
Výška je nakreslená z vrcholu rovnoramenného trojuholníka, ktorý tvorí pravý uhol a dva zhodné trojuholníky. Výsledkom je, že výška rozdeľuje základňu na dva rovnaké segmenty. Dĺžka výšky je 18 palcov a dĺžka základne je 15 palcov. Nájdite obvod trojuholn - Rebrík 14
 Rebrík dĺžky 3,4 m je opretý o stenu. Jeho dolný koniec je od steny vzdialeny 1,6m. V akej výške sa rebrík dotýka steny?
Rebrík dĺžky 3,4 m je opretý o stenu. Jeho dolný koniec je od steny vzdialeny 1,6m. V akej výške sa rebrík dotýka steny? - Ako zistím
 Ako zistím uhlopriečky kosoštvorca, ak jeho obvod je 80dm a jedna uhlopriečka je 2x väčšia ako druhá?
Ako zistím uhlopriečky kosoštvorca, ak jeho obvod je 80dm a jedna uhlopriečka je 2x väčšia ako druhá? - Na vrchole 2
 Na vrchole kopca stojí rozhľadňa 30 m vysoká. Jej pätu a vrchol vidíme z určitého miesta v údolí pod výškovými uhlami a= 28°30", b=30°40". Ako vysoko je vrchol kopca nad horizontálnou rovinou pozorovacieho miesta?
Na vrchole kopca stojí rozhľadňa 30 m vysoká. Jej pätu a vrchol vidíme z určitého miesta v údolí pod výškovými uhlami a= 28°30", b=30°40". Ako vysoko je vrchol kopca nad horizontálnou rovinou pozorovacieho miesta? - Daný je 8
 Daný je rovnobežnik KLMN, v ktorom poznáme veľkosti strán/KL/ = a = 84,5 cm, /KN/ = 47,8 cm a veľkosť uhla pri vrchole K 56°40´. Vypočítajte veľkosť uhlopriečok.
Daný je rovnobežnik KLMN, v ktorom poznáme veľkosti strán/KL/ = a = 84,5 cm, /KN/ = 47,8 cm a veľkosť uhla pri vrchole K 56°40´. Vypočítajte veľkosť uhlopriečok. - Vypočítajte 253
 Vypočítajte výšku stožiaru, ktorého pätu vidíme v hĺbkovom uhle 11° a vrchol vo výškovom uhle 28°. Stožiar je pozorovaný z miesta 10 m nad úrovňou päty stožiara.
Vypočítajte výšku stožiaru, ktorého pätu vidíme v hĺbkovom uhle 11° a vrchol vo výškovom uhle 28°. Stožiar je pozorovaný z miesta 10 m nad úrovňou päty stožiara.
