V Kocúrkove - Z8-I-6 2019 MO
V Kocúrkove používajú mince iba s dvoma hodnotami, ktoré sú vyjadrené v kocúrkovských korunách kladnými celými číslami. Pomocou dostatočného množstva takých mincí je možné zaplatiť akúkoľvek celočíselnú sumu väčšiu ako 53 kocúrkovských korún, a to presne a bez vydávania. Sumu 53 kocúrkovských korún však bez vydávania zaplatiť nemožno. Zistite, ktoré hodnoty mohli byť na kocúrkovských minciach. Určte aspoň dve riešenia.
Správna odpoveď:

Zobrazujem 13 komentárov:
Markie
2, 55
3, 28
4, 19
7, 10
ale musim povedat, ze k tejto ulohe neviem urobit nejaky elegantny postup...
nemam rad ulohy, kde treba skusat...
3, 28
4, 19
7, 10
ale musim povedat, ze k tejto ulohe neviem urobit nejaky elegantny postup...
nemam rad ulohy, kde treba skusat...
4 roky 2 Likes
Franta
Frobeniovo číslo
Problém mincí (označovaný také jako problém frobenské mince nebo Frobeniův problém po matematikovi Ferdinandu Frobeniovi) je matematický problém, který hledá největší peněžní částku, kterou nelze získat pouze pomocí mincí určených nominálních hodnot. Například největší částka, kterou nelze získat pouze pomocí mincí 3 a 5 jednotek, je 7 jednotek.
Řešení tohoto problému pro danou sadu nominálních hodnot mincí se nazývá Frobeniovo číslo.
Frobeniovo číslo existuje, pokud sada nominálních hodnot mincí nemá společný dělitel větší než 1.
Pokud existují pouze dvě různé nominální hodnoty mincí x a y, potom pro Frobeniovo číslo existuje explicitní vzorec: xy − x − y.
Tento vzorec objevil James Joseph Sylvester v roce 1882.
Známe Frobeniovo číslo: 53, a máme určit x a y. Tedy:
xy – x – y = 53
xy – x – y + 1 = 53 + 1
x(y – 1) – (y – 1) = 54
(y – 1)(x – 1) = 54
Možné dvojice:
2 a 27, to je y = 3, x = 28
3 a 18, to je y = 4, x = 19
6 a 9, to je y = 7, x = 10
Problém mincí (označovaný také jako problém frobenské mince nebo Frobeniův problém po matematikovi Ferdinandu Frobeniovi) je matematický problém, který hledá největší peněžní částku, kterou nelze získat pouze pomocí mincí určených nominálních hodnot. Například největší částka, kterou nelze získat pouze pomocí mincí 3 a 5 jednotek, je 7 jednotek.
Řešení tohoto problému pro danou sadu nominálních hodnot mincí se nazývá Frobeniovo číslo.
Frobeniovo číslo existuje, pokud sada nominálních hodnot mincí nemá společný dělitel větší než 1.
Pokud existují pouze dvě různé nominální hodnoty mincí x a y, potom pro Frobeniovo číslo existuje explicitní vzorec: xy − x − y.
Tento vzorec objevil James Joseph Sylvester v roce 1882.
Známe Frobeniovo číslo: 53, a máme určit x a y. Tedy:
xy – x – y = 53
xy – x – y + 1 = 53 + 1
x(y – 1) – (y – 1) = 54
(y – 1)(x – 1) = 54
Možné dvojice:
2 a 27, to je y = 3, x = 28
3 a 18, to je y = 4, x = 19
6 a 9, to je y = 7, x = 10
Slniecko
V texte sa píše:" Pomocou dostatočného množstva takých mincí je možné zaplatiť akúkoľvek celočíselnú sumu väčšiu ako 53 kocúrkovských korún, a to presne a bez vydávania." Ako viete pomocou mincí napr. 3 a 28 zaplatiť sumu 54?
Matematik
3*9+28*1=55
... zasnem ze si ludia aspon elementarne overenie toho co tvrdia nevyskusaju na kalkulacke,,, alebo na internete:
https://www.hackmath.net/sk/kalkulacka/celociselne-diofantove-rovnice?input=3a%2B28b%3D55&submit=Vypo%C4%8D%C3%ADtaj
Je to ako pravo volit - ma ho kazdy. Ludia volia pocitmi, emociami, cize si zvolia zlych zastupcov... Pripadne takych ktory ich uplatia predvolebnou korupciou (zvysenie dochodkov, 13. dochodok...). Urcite by pravo volit malo byt nejak zmenene, napr. kazdy hlas by mal vahu rocnych dani ktore plati volič štátu. Kto platí málo, jeho hlas bude oslabený. Kto neplatí nič, bude mať nulový hlas.To bu potom do parlamentu neboli populisti vobec zvoleny.
... zasnem ze si ludia aspon elementarne overenie toho co tvrdia nevyskusaju na kalkulacke,,, alebo na internete:
https://www.hackmath.net/sk/kalkulacka/celociselne-diofantove-rovnice?input=3a%2B28b%3D55&submit=Vypo%C4%8D%C3%ADtaj
Je to ako pravo volit - ma ho kazdy. Ludia volia pocitmi, emociami, cize si zvolia zlych zastupcov... Pripadne takych ktory ich uplatia predvolebnou korupciou (zvysenie dochodkov, 13. dochodok...). Urcite by pravo volit malo byt nejak zmenene, napr. kazdy hlas by mal vahu rocnych dani ktore plati volič štátu. Kto platí málo, jeho hlas bude oslabený. Kto neplatí nič, bude mať nulový hlas.To bu potom do parlamentu neboli populisti vobec zvoleny.
Matematik
tak skusme: 54 = 55a+2b
a = 55b+2c
a>53
a<70
b>=0
c>=0
a1=54, b1=0, c1=27
a2=55, b2=1, c2=0
a3=56, b3=0, c3=28
a4=57, b4=1, c4=1
a5=58, b5=0, c5=29
a6=59, b6=1, c6=2
a7=60, b7=0, c7=30
a8=61, b8=1, c8=3
a9=62, b9=0, c9=31
a10=63, b10=1, c10=4
a11=64, b11=0, c11=32
a12=65, b12=1, c12=5
a13=66, b13=0, c13=33
a14=67, b14=1, c14=6
a15=68, b15=0, c15=34
a16=69, b16=1, c16=7
cize bingo... mozno jsme to zbytocne obmedzili ze obe mince musi byt mensi nez nebo rovne 53 ...
a = 55b+2c
a>53
a<70
b>=0
c>=0
a1=54, b1=0, c1=27
a2=55, b2=1, c2=0
a3=56, b3=0, c3=28
a4=57, b4=1, c4=1
a5=58, b5=0, c5=29
a6=59, b6=1, c6=2
a7=60, b7=0, c7=30
a8=61, b8=1, c8=3
a9=62, b9=0, c9=31
a10=63, b10=1, c10=4
a11=64, b11=0, c11=32
a12=65, b12=1, c12=5
a13=66, b13=0, c13=33
a14=67, b14=1, c14=6
a15=68, b15=0, c15=34
a16=69, b16=1, c16=7
cize bingo... mozno jsme to zbytocne obmedzili ze obe mince musi byt mensi nez nebo rovne 53 ...
Tipy na súvisiace online kalkulačky
Riešite Diofantovské problémy a hľadáte kalkulačku diofantovských celočíselných rovníc?
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Chcete previesť delenie prirodzených čísel - zistiť podiel a zvyšok?
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Chcete previesť delenie prirodzených čísel - zistiť podiel a zvyšok?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- množiny
- rovnica
- celočíselná rovnica
- prvočísla
- prienik množín
- aritmetika
- delenie
- základné funkcie
- úvaha
- čísla
- prirodzené čísla
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- MO Z7–I–3 2019
 Roman má rád kúzla a matematiku. Naposledy čaroval s trojcifernými alebo štvorcifernými číslami takto: • z daného čísla vytvoril dve pomocné čísla tak, že ho rozdelil medzi ciframi na mieste stoviek a desiatok (napr. Z čísla 581 by dostal 5 a 81), • pomoc
Roman má rád kúzla a matematiku. Naposledy čaroval s trojcifernými alebo štvorcifernými číslami takto: • z daného čísla vytvoril dve pomocné čísla tak, že ho rozdelil medzi ciframi na mieste stoviek a desiatok (napr. Z čísla 581 by dostal 5 a 81), • pomoc - MO B 2019 - uloha 2
 Prirodzené číslo n má aspoň 73 dvojciferných deliteľov. Dokážte, že jedným z nich je číslo 60. Uveďte tiež príklad čísla n, ktoré má práve 73 dvojciferných deliteľov, vrátane náležitého zdôvodnenia.
Prirodzené číslo n má aspoň 73 dvojciferných deliteľov. Dokážte, že jedným z nich je číslo 60. Uveďte tiež príklad čísla n, ktoré má práve 73 dvojciferných deliteľov, vrátane náležitého zdôvodnenia. - Olympiády
 Z 50 žiakov 44 riešilo aspoň jednu z olympiád - MO matematická olympiáda, BO biologická olympiáda. MO neriešilo 20 žiakov. Tých, čo riešili obidve olympiády, bola 1/3 z tých, čo riešili práve jednu olympiádu. Koľko žiakov riešilo len MO, len BO? Koľkí rie
Z 50 žiakov 44 riešilo aspoň jednu z olympiád - MO matematická olympiáda, BO biologická olympiáda. MO neriešilo 20 žiakov. Tých, čo riešili obidve olympiády, bola 1/3 z tých, čo riešili práve jednu olympiádu. Koľko žiakov riešilo len MO, len BO? Koľkí rie - MO Z9-I-3 2018
 V našom meste sú tri kiná, ktorým sa hovorí podľa svetových strán. O ich otváracích hodinách je známe, že: • každý deň je otvorené aspoň jedno kino, • ak je otvorené južné kino, tak nie je otvorené severné kino, • nikdy nie je otvorené súčasne severné a v
V našom meste sú tri kiná, ktorým sa hovorí podľa svetových strán. O ich otváracích hodinách je známe, že: • každý deň je otvorené aspoň jedno kino, • ak je otvorené južné kino, tak nie je otvorené severné kino, • nikdy nie je otvorené súčasne severné a v - Matematická súťaž
 V matematickej súťaži riešili jej účastníci dve úlohy. Každý vyriešil aspoň jednu úlohu, pritom prvú úlohu vyriešilo 80 % účastníkov, druhú úlohu 50 %. Obidve úlohy vyriešilo 60 účastníkov. Koľko účastníkov mala súťaž?
V matematickej súťaži riešili jej účastníci dve úlohy. Každý vyriešil aspoň jednu úlohu, pritom prvú úlohu vyriešilo 80 % účastníkov, druhú úlohu 50 %. Obidve úlohy vyriešilo 60 účastníkov. Koľko účastníkov mala súťaž? - Komora
 V komore, kde sa rozbilo svetlo a všetko z nej musíme brať naslepo, máme ponožky štyroch rôznych farieb. Ak si chceme byť istí, že vytiahneme aspoň dve biele ponožky, musíme ich z komory priniesť 28. Aby sme mali takú istotu pre sivé ponožky, musíme ich p
V komore, kde sa rozbilo svetlo a všetko z nej musíme brať naslepo, máme ponožky štyroch rôznych farieb. Ak si chceme byť istí, že vytiahneme aspoň dve biele ponožky, musíme ich z komory priniesť 28. Aby sme mali takú istotu pre sivé ponožky, musíme ich p - Prienik či zjednotenie
 V triede je 24 žiakov. psa má doma 11 z nich. Drobného hlodavca má 15 z nich. Žiadne zvieratko nemá doma 5 žiakov. Koľko žiakov má doma 2 zvieratká?
V triede je 24 žiakov. psa má doma 11 z nich. Drobného hlodavca má 15 z nich. Žiadne zvieratko nemá doma 5 žiakov. Koľko žiakov má doma 2 zvieratká? - Trojuholníkov 83111
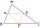 Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru
Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru - Priklad – 8. rocnik (asi MO)
 Adam napı́sal nasledujúci súčet s piatimi tajnými sčı́tancami: a + bb + ccc + dddd + eeeee. Prezradil, že znaky „a, b, c, d, e“ predstavujú navzájom rôzne cifry 1, 2, 3, 4, 5 a že výsledný súčet je deliteľný 11. Ktoré najmenšie a ktoré na
Adam napı́sal nasledujúci súčet s piatimi tajnými sčı́tancami: a + bb + ccc + dddd + eeeee. Prezradil, že znaky „a, b, c, d, e“ predstavujú navzájom rôzne cifry 1, 2, 3, 4, 5 a že výsledný súčet je deliteľný 11. Ktoré najmenšie a ktoré na - Mo z5 2023 psy
 Anetkin strýko má narodeniny v rovnaký deň v roku ako Anetkin teta. Strýko je starší ako teta, nie však o viac ako o desať rokov, a obaja sú plnoletí. Na poslednej oslave ich narodenín si Anetka uvedomila, že keď vynásobí ich oslavované veky a výsledný sú
Anetkin strýko má narodeniny v rovnaký deň v roku ako Anetkin teta. Strýko je starší ako teta, nie však o viac ako o desať rokov, a obaja sú plnoletí. Na poslednej oslave ich narodenín si Anetka uvedomila, že keď vynásobí ich oslavované veky a výsledný sú - Trojuholník MO Z8-I-5
 Trojuholník ABC je rozdelený úsečkami. Úsečky DE a AB sú rovnobežné. Trojuholníky CDH, CHI, CIE, FIH majú rovnaký obsah a to 8 dm². Zistite obsah štvoruholníka AFHD.
Trojuholník ABC je rozdelený úsečkami. Úsečky DE a AB sú rovnobežné. Trojuholníky CDH, CHI, CIE, FIH majú rovnaký obsah a to 8 dm². Zistite obsah štvoruholníka AFHD. - Zajac 2024m
 Zajac sa zúčastnil na pretekoch dlhých 2024 metrov. Zo štartovej čiary sa odrazil ľavou nohou a po celý čas pretekov pravidelne striedal ľavú, pravú a obe nohy. Keď sa zajac odrazil ľavou nohou, skočil 35 dm, keď sa odrazil pravou nohou, skočil 15
Zajac sa zúčastnil na pretekoch dlhých 2024 metrov. Zo štartovej čiary sa odrazil ľavou nohou a po celý čas pretekov pravidelne striedal ľavú, pravú a obe nohy. Keď sa zajac odrazil ľavou nohou, skočil 35 dm, keď sa odrazil pravou nohou, skočil 15 - Uvedených 82574
 Do krúžku chodí 29 detí. 11 uviedlo, že má doma psa, 14 detí má doma mačku a 12 detí má doma škrečka. Dve deti majú všetky tri zvieratká. 7 detí nemá doma žiadne zviera. . Koľko detí má aspoň dve z uvedených zvierat? Koľko detí má práve jedno z uvedených
Do krúžku chodí 29 detí. 11 uviedlo, že má doma psa, 14 detí má doma mačku a 12 detí má doma škrečka. Dve deti majú všetky tri zvieratká. 7 detí nemá doma žiadne zviera. . Koľko detí má aspoň dve z uvedených zvierat? Koľko detí má práve jedno z uvedených - Karol 9
 Karol mal vynásobiť dve dvojciferné čísla. Z nepozornosti vymenil poradie cifier v jednom z činiteľov a dostal súčin, ktorý bol o 4 248 menší ako správny výsledok. Aký je správny výsledok? Koľko malo Karolovi správne vyjsť?
Karol mal vynásobiť dve dvojciferné čísla. Z nepozornosti vymenil poradie cifier v jednom z činiteľov a dostal súčin, ktorý bol o 4 248 menší ako správny výsledok. Aký je správny výsledok? Koľko malo Karolovi správne vyjsť? - MO 2023
 V záhradkarskej osade mal pán Jahoda vo svojom sude 16.litrov vody. Sused Malina mal vo svojom sude tri krát viac vody, ako pán Jahoda. Začalo pršať a do oboch sudov napršalo rovnaké množstvo vody. Po daždi pán Malina zistil, že má v sude dvakrát viac vod
V záhradkarskej osade mal pán Jahoda vo svojom sude 16.litrov vody. Sused Malina mal vo svojom sude tri krát viac vody, ako pán Jahoda. Začalo pršať a do oboch sudov napršalo rovnaké množstvo vody. Po daždi pán Malina zistil, že má v sude dvakrát viac vod - Adam mal 3
 Adam mal papier, ktorý bol natoľko veľký, že by sa z neho dalo natrhať niekoľko desiatok tisíc kúskov. Najprv papier roztrhal na štyri kúsky. Každý z týchto kú skov vzal a roztrhal buď na štyri, alebo na desať kúskov. Rovnakým spôsobom pokračo
Adam mal papier, ktorý bol natoľko veľký, že by sa z neho dalo natrhať niekoľko desiatok tisíc kúskov. Najprv papier roztrhal na štyri kúsky. Každý z týchto kú skov vzal a roztrhal buď na štyri, alebo na desať kúskov. Rovnakým spôsobom pokračo - Skautskom MO 2023 z8
 V minulom roku bolo v našom skautskom oddiele o 30 chlapcov viac ako dievčat. Tento rok sa počet detí v oddiele zväčšil o 10%, pričom počet chlapcov sa zväčšil o 5% a počet dievčat sa zväčšil o 20%. Koľko detí máme tento rok v oddiele?
V minulom roku bolo v našom skautskom oddiele o 30 chlapcov viac ako dievčat. Tento rok sa počet detí v oddiele zväčšil o 10%, pričom počet chlapcov sa zväčšil o 5% a počet dievčat sa zväčšil o 20%. Koľko detí máme tento rok v oddiele?
