MO Z9-I-6 2019
Kristína zvolila isté nepárne prirodzené číslo deliteľné tromi. Jakub s Dávidom potom skúmali trojuholníky, ktoré majú obvod v milimetroch rovný Kristínou zvolenému číslu a ktorých strany majú dĺžky v milimetroch vyjadrené navzájom rôznymi celými číslami.
Jakub našiel taký trojuholník, v ktorom najdlhšia zo strán má najväčšiu možnú dĺžku, a túto hodnotu zapísal na tabuľu. Dávid našiel taký trojuholník, v ktorom najkratšia zo strán má najväčšiu možnú dĺžku, a túto hodnotu tiež zapísal na tabuľu. Kristína obe dĺžky na tabuli správne sčítala a vyšlo jej 1 681 mm. Určte, ktoré číslo Kristína zvolila.
Jakub našiel taký trojuholník, v ktorom najdlhšia zo strán má najväčšiu možnú dĺžku, a túto hodnotu zapísal na tabuľu. Dávid našiel taký trojuholník, v ktorom najkratšia zo strán má najväčšiu možnú dĺžku, a túto hodnotu tiež zapísal na tabuľu. Kristína obe dĺžky na tabuli správne sčítala a vyšlo jej 1 681 mm. Určte, ktoré číslo Kristína zvolila.
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Riešite Diofantovské problémy a hľadáte kalkulačku diofantovských celočíselných rovníc?
Chcete zaokrúhliť číslo?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Riešite Diofantovské problémy a hľadáte kalkulačku diofantovských celočíselných rovníc?
Chcete zaokrúhliť číslo?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Koreň
 Koreň rovnice (x-5)² +26 = x² +27x je rovný nula, alebo väčší ako 0, alebo menší ako 0? ...
Koreň rovnice (x-5)² +26 = x² +27x je rovný nula, alebo väčší ako 0, alebo menší ako 0? ... - Dokonalý štvorec
 Klasifikovali by ste 324 ako dokonalý štvorec, dokonalú kocku, oboje alebo ani jedno? ...
Klasifikovali by ste 324 ako dokonalý štvorec, dokonalú kocku, oboje alebo ani jedno? ... - Výraz zátvorky
 Ktorý výraz sa rovná 12? ...
Ktorý výraz sa rovná 12? ... - Rybárskych 48553
 Marek mal 325 Kč. Kúpil si za 129 Kč tričko, v rybárskych potrebách chcel minúť 276 Kč. Koľko Kč (česká koruna) mu na rybárske potreby pridali rodičia? Koľko týždňov mu krátili o 10 Kč vreckové, než splatil dlh?
Marek mal 325 Kč. Kúpil si za 129 Kč tričko, v rybárskych potrebách chcel minúť 276 Kč. Koľko Kč (česká koruna) mu na rybárske potreby pridali rodičia? Koľko týždňov mu krátili o 10 Kč vreckové, než splatil dlh? - Myslel až vymyslel
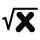 Anton povedal: Mám prirodzené číslo x. Keď ho umocním na štyri tretiny, dostanem trikrát vačšie číslo. Aké číslo Anton myslel?
Anton povedal: Mám prirodzené číslo x. Keď ho umocním na štyri tretiny, dostanem trikrát vačšie číslo. Aké číslo Anton myslel? - Mocnina
 Číslo left(sqrt(12 * sqrt[ 9 ] (12)) right) 14 možno zapísať v tvare 12^x. Nájdite hodnotu x.
Číslo left(sqrt(12 * sqrt[ 9 ] (12)) right) 14 možno zapísať v tvare 12^x. Nájdite hodnotu x. - Miestny
 Miestny univerzitný basketbalový tím ponúka autobusovú dopravu na zápas. Každý autobus má kapacitu 56 osôb. Celkovo sa prihlásilo 328 ľudí. Všetky autobusy sú plné okrem posledného autobusu. Koľko autobusov sa použije? Otázka 2: Koľko ľudí je v poslednom
Miestny univerzitný basketbalový tím ponúka autobusovú dopravu na zápas. Každý autobus má kapacitu 56 osôb. Celkovo sa prihlásilo 328 ľudí. Všetky autobusy sú plné okrem posledného autobusu. Koľko autobusov sa použije? Otázka 2: Koľko ľudí je v poslednom - Vypočítaj 435
 Vypočítaj hodnotu výrazu V = 3x²- 2x + 3 pre x = -2.
Vypočítaj hodnotu výrazu V = 3x²- 2x + 3 pre x = -2. - Nájdite 15
 Nájdite najmenšie x prirodzené také, že 2x je štvorec a 3x je tretia mocnina prirodzeného čísla
Nájdite najmenšie x prirodzené také, že 2x je štvorec a 3x je tretia mocnina prirodzeného čísla - Nasledujúci 49683
 (a) Preveďte nasledujúce zmiešané čísla na nesprávne zlomky. i. 3 5/8 ii. 7 7/6 (b) Preveďte nasledujúci nesprávny zlomok na zmiešané číslo. i. 13/4 ii. 78/5 (c) Zjednodušte tieto zlomky na najnižších členov. i. 36/42 ii. 27/45 2. vyhodnoťte nasledujúce v
(a) Preveďte nasledujúce zmiešané čísla na nesprávne zlomky. i. 3 5/8 ii. 7 7/6 (b) Preveďte nasledujúci nesprávny zlomok na zmiešané číslo. i. 13/4 ii. 78/5 (c) Zjednodušte tieto zlomky na najnižších členov. i. 36/42 ii. 27/45 2. vyhodnoťte nasledujúce v - Rozdielu 46651
 Nájdete súčin podielu a rozdielu čísel 16/3 a 3,2
Nájdete súčin podielu a rozdielu čísel 16/3 a 3,2 - Vypočítajte 45311
 Vypočítajte súčin súčtu a rozdielu čísel odmocnina 5 a odmocnina 3 ( v tomto poradí)
Vypočítajte súčin súčtu a rozdielu čísel odmocnina 5 a odmocnina 3 ( v tomto poradí) - Zlomky: 42141
 Zlomky: 14/17 . 34/56 + 6/9 + 10/13 : 5/26 = 10/16 - ¼ + 15/18 : 5/9 = ¾ . (25/42 - 3/7) +16/21 : 4/7 = 2. Celé čísla: (-12) + (-6). (-2) - (-14) : 2 = 35 : (-5) + (-12) . 2 + (-6) = 42 : (-3) . (-5) - (-12)+ (-16) =
Zlomky: 14/17 . 34/56 + 6/9 + 10/13 : 5/26 = 10/16 - ¼ + 15/18 : 5/9 = ¾ . (25/42 - 3/7) +16/21 : 4/7 = 2. Celé čísla: (-12) + (-6). (-2) - (-14) : 2 = 35 : (-5) + (-12) . 2 + (-6) = 42 : (-3) . (-5) - (-12)+ (-16) = - Znamienka 40171
 Doplň znamienka, aby platilo 5 5 5 5 5=14
Doplň znamienka, aby platilo 5 5 5 5 5=14 - Koľko 81
 Koľko celých čísel je väčších ako 547/3 a menších ako 931/4?
Koľko celých čísel je väčších ako 547/3 a menších ako 931/4? - O koľko 9
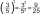 O koľko je polovica z polovice väčšia ako tretia mocnina polovice?
O koľko je polovica z polovice väčšia ako tretia mocnina polovice? - Vnučka
 V roku 2014 bol súčet veku Milkynej tety, jej dcéry a jej vnučky rovný 100 rokov. V ktorom roku sa narodila vnučka, ak vieme, že vek každej z nich možno vyjadriť ako mocnina dvoch?
V roku 2014 bol súčet veku Milkynej tety, jej dcéry a jej vnučky rovný 100 rokov. V ktorom roku sa narodila vnučka, ak vieme, že vek každej z nich možno vyjadriť ako mocnina dvoch?
