MO Z9-I-6 2019
Kristína zvolila isté nepárne prirodzené číslo deliteľné tromi. Jakub s Dávidom potom skúmali trojuholníky, ktoré majú obvod v milimetroch rovný Kristínou zvolenému číslu a ktorých strany majú dĺžky v milimetroch vyjadrené navzájom rôznymi celými číslami.
Jakub našiel taký trojuholník, v ktorom najdlhšia zo strán má najväčšiu možnú dĺžku, a túto hodnotu zapísal na tabuľu. Dávid našiel taký trojuholník, v ktorom najkratšia zo strán má najväčšiu možnú dĺžku, a túto hodnotu tiež zapísal na tabuľu. Kristína obe dĺžky na tabuli správne sčítala a vyšlo jej 1 681 mm. Určte, ktoré číslo Kristína zvolila.
Jakub našiel taký trojuholník, v ktorom najdlhšia zo strán má najväčšiu možnú dĺžku, a túto hodnotu zapísal na tabuľu. Dávid našiel taký trojuholník, v ktorom najkratšia zo strán má najväčšiu možnú dĺžku, a túto hodnotu tiež zapísal na tabuľu. Kristína obe dĺžky na tabuli správne sčítala a vyšlo jej 1 681 mm. Určte, ktoré číslo Kristína zvolila.
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Riešite Diofantovské problémy a hľadáte kalkulačku diofantovských celočíselných rovníc?
Chcete zaokrúhliť číslo?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Riešite Diofantovské problémy a hľadáte kalkulačku diofantovských celočíselných rovníc?
Chcete zaokrúhliť číslo?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Štvoruholník
 Ukážte, že štvoruholník s vrcholmi P1 (0,1), P2 (4,2) P3 (3,6) P4 (-5,4) má dva pravé trojuholníky.
Ukážte, že štvoruholník s vrcholmi P1 (0,1), P2 (4,2) P3 (3,6) P4 (-5,4) má dva pravé trojuholníky. - Určte 9
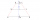 Určte vzdialenosť dvoch neprístupných miest P, Q, ak vzdialenosť dvoch pozorovacích miest A, B je 2000m a ak poznáte veľkosť uhlov QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažované miesta A, B, P, Q ležia v jednej rovine.
Určte vzdialenosť dvoch neprístupných miest P, Q, ak vzdialenosť dvoch pozorovacích miest A, B je 2000m a ak poznáte veľkosť uhlov QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažované miesta A, B, P, Q ležia v jednej rovine. - Obsah kruhu
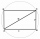 Vypočítajte obsah kruhu, ktorý má rovnaký obvod ako je obvod obdĺžnika vpísanej kružnici s polomerom r 9 cm tak, že jeho strany sú v pomere 2 ku 7.
Vypočítajte obsah kruhu, ktorý má rovnaký obvod ako je obvod obdĺžnika vpísanej kružnici s polomerom r 9 cm tak, že jeho strany sú v pomere 2 ku 7. - Medzikružie
 Štvorcu o strane a = 1 je vpísaná a opísaná kružnica. Určte obsah medzikružia.
Štvorcu o strane a = 1 je vpísaná a opísaná kružnica. Určte obsah medzikružia. - Štvrťkruh 4
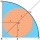 Aký polomer má kruh vpisany do štvrťkruhu s polomerom 100 cm?
Aký polomer má kruh vpisany do štvrťkruhu s polomerom 100 cm? - Valec naležato
 Valec s priemerom 3m a výškou/dĺžkou 15 m je položený naležato. Je doň napustená voda, ktorá siaha do výšky 60 cm pod os valca. Koľko hektolitrov vody je vo valci?
Valec s priemerom 3m a výškou/dĺžkou 15 m je položený naležato. Je doň napustená voda, ktorá siaha do výšky 60 cm pod os valca. Koľko hektolitrov vody je vo valci? - Rovnobežník - uhlopriečky
 Vypočítajte obsah rovnobežníka, ak sú veľkosti strán a=80, b=60 a veľkosť uhla zovretého uhlopriečkami je 60°.
Vypočítajte obsah rovnobežníka, ak sú veľkosti strán a=80, b=60 a veľkosť uhla zovretého uhlopriečkami je 60°. - Odsek a oblúk
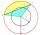 Vypočítaj plochu S odseku a dľžku kružnicového oblúka l . Výška odseku je 2 cm a uhol α=60°. Pomôcka: S=1/2 r² . (β-sinβ)
Vypočítaj plochu S odseku a dľžku kružnicového oblúka l . Výška odseku je 2 cm a uhol α=60°. Pomôcka: S=1/2 r² . (β-sinβ) - Medzikružie
 Štvorcu o obsahu 16 centimetrov štvorcových je vpísaná kružnica k1 a opísaná kružnica k2. Vypočítajte obsah medzikružia, ktoré kružnice k1, k2 ohraničujú.
Štvorcu o obsahu 16 centimetrov štvorcových je vpísaná kružnica k1 a opísaná kružnica k2. Vypočítajte obsah medzikružia, ktoré kružnice k1, k2 ohraničujú. - Kruhový bazén
 Podstava bazéna má tvar kruhu s polomerom r=10m okrem kruhového odseku, ktorý určuje tetiva dĺžky 10m. Jeho hĺbka je h=2m. Koľko hektolitrov vody sa zmesti do bazéna?
Podstava bazéna má tvar kruhu s polomerom r=10m okrem kruhového odseku, ktorý určuje tetiva dĺžky 10m. Jeho hĺbka je h=2m. Koľko hektolitrov vody sa zmesti do bazéna? - V trojuholníku 18
 V trojuholníku ABC je dané b=5 cm, c=6 cm, /BAC/ = 80°. Vypočítajte veľkosti ostatných strán a uhlov, ďalej určte veľkosti ťažnice tc a obsah trojuholníka.
V trojuholníku ABC je dané b=5 cm, c=6 cm, /BAC/ = 80°. Vypočítajte veľkosti ostatných strán a uhlov, ďalej určte veľkosti ťažnice tc a obsah trojuholníka. - V trojuholníku 10
 V trojuholníku ABC vypočítajte veľkosti všetkých výšok, uhlov, obvod a obsah, ak je dané a-40cm, b-57cm, c-59cm
V trojuholníku ABC vypočítajte veľkosti všetkých výšok, uhlov, obvod a obsah, ak je dané a-40cm, b-57cm, c-59cm - Vypočítajte 52
 Vypočítajte obvod a obsah obdĺžnika, ak jeho uhlopriečka má dĺžku 14 cm a uhlopriečky zvierajú uhol 130°.
Vypočítajte obvod a obsah obdĺžnika, ak jeho uhlopriečka má dĺžku 14 cm a uhlopriečky zvierajú uhol 130°. - Plášť
 Plášť kužeľa je vytvorený zvinutím kruhového výseku s polomerom 1. Pre aký stredový uhol daného kruhového výseku bude objem vzniknutého kužeľa maximálnu?
Plášť kužeľa je vytvorený zvinutím kruhového výseku s polomerom 1. Pre aký stredový uhol daného kruhového výseku bude objem vzniknutého kužeľa maximálnu? - Štvorboký ihlan - objem a povrch
 V pravidelnom štvorbokom ihlane je výška 6,5 cm a uhol medzi podstavou a bočnou stenou je 42°. Vypočítaj povrch a objem telesa. Výpočty zaokrúhliť na 1 desatinné miesto.
V pravidelnom štvorbokom ihlane je výška 6,5 cm a uhol medzi podstavou a bočnou stenou je 42°. Vypočítaj povrch a objem telesa. Výpočty zaokrúhliť na 1 desatinné miesto. - Kosý hranol
 Aký objem má štvorboký kosý hranol s podstavnými hranami o dĺžke a = 1m, b = 1,1m, c = 1,2 m, d = 0,7m, ak bočná hrana s dĺžkou h = 3,9m má odchýlku od podstavy 20° 35 'a hrany a, b zvierajú uhol 50,5°.
Aký objem má štvorboký kosý hranol s podstavnými hranami o dĺžke a = 1m, b = 1,1m, c = 1,2 m, d = 0,7m, ak bočná hrana s dĺžkou h = 3,9m má odchýlku od podstavy 20° 35 'a hrany a, b zvierajú uhol 50,5°. - Kvietok
 Štvorcu bol opísaný kruh a nad každou stranou štvorca, ako nad priemerom, bol vyznačený polkruh. Vznikli tak 4 lupienky. Čo je väčšie: obsah stredného štvorca, alebo obsah štyroch lupienkov?
Štvorcu bol opísaný kruh a nad každou stranou štvorca, ako nad priemerom, bol vyznačený polkruh. Vznikli tak 4 lupienky. Čo je väčšie: obsah stredného štvorca, alebo obsah štyroch lupienkov?
