Hokejisti
Po vystriedaní si na striedačke náhodne sadlo vedľa seba päť hokejistov. Aká je
pravdepodobnosť, že dvaja najlepší strelci z tejto pätice budú sedieť vedľa seba?
pravdepodobnosť, že dvaja najlepší strelci z tejto pätice budú sedieť vedľa seba?
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku permutácií.
Pozrite aj našu kalkulačku variácií.
Chceš si dať zrátať kombinačné číslo?
Pozrite aj našu kalkulačku variácií.
Chceš si dať zrátať kombinačné číslo?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Päť hostí
 Koľkými spôsobmi môžeme usadiť za stôl päť hostí, z ktorých dvaja sú manželia a chcú sedieť vedľa seba?
Koľkými spôsobmi môžeme usadiť za stôl päť hostí, z ktorých dvaja sú manželia a chcú sedieť vedľa seba? - Vlajky
 Koľko 4 farebných vlajok možno vytvoriť z 5 farieb tak, aby každá vlajka sa skladala z troch rôznych farieb?
Koľko 4 farebných vlajok možno vytvoriť z 5 farieb tak, aby každá vlajka sa skladala z troch rôznych farieb? - Koľkými 16
 Koľkými spôsobmi môže 10 áut zaparkovať vedľa seba na parkovisku?
Koľkými spôsobmi môže 10 áut zaparkovať vedľa seba na parkovisku? - Peter 21
 Peter, Jano, Alica a Rebeka išli na koncert vážnej hudby. Koľkými rôznými spôsobmi sa môžu usadiť na štyri voľné sedadlá ak Rebeka chce sedieť pri Janovi?
Peter, Jano, Alica a Rebeka išli na koncert vážnej hudby. Koľkými rôznými spôsobmi sa môžu usadiť na štyri voľné sedadlá ak Rebeka chce sedieť pri Janovi?
- Marián
 Marián dostal v priebehu jedného dňa dve rôzne známky. Koľko je možností pre známky, ktoré mohol dostať?
Marián dostal v priebehu jedného dňa dve rôzne známky. Koľko je možností pre známky, ktoré mohol dostať? - V počítačovej
 V počítačovej hre je potrebné pozbierať v miestnosti 5 predmetov: meč, prsteň, obraz, kľúč a mincu. Záleží na poradí, v akom jednotlivé predmety pozbierame, pri zlom poradí prídeme o život . Koľko je všetkých poradí?
V počítačovej hre je potrebné pozbierať v miestnosti 5 predmetov: meč, prsteň, obraz, kľúč a mincu. Záleží na poradí, v akom jednotlivé predmety pozbierame, pri zlom poradí prídeme o život . Koľko je všetkých poradí? - S faktoriálom
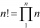 Vykráť výraz s faktoriálmi: 12! x 2 x 7! / 6 x 10! 8!
Vykráť výraz s faktoriálmi: 12! x 2 x 7! / 6 x 10! 8! - Koľkými 10
 Koľkými spôsobmi môže uložiť na poličku vedľa seba 7 rôznych kníh, keď kniha z matematiky musí byť na kraji police?
Koľkými spôsobmi môže uložiť na poličku vedľa seba 7 rôznych kníh, keď kniha z matematiky musí byť na kraji police? - Janka 7
 Janka si chce usporiadat na policku 4 anglicke a 3 slovenske knihy tak, aby boli zoradené najprv anglicke a potom slovenske knihy . Kolkymi sposobmi to moze urobit?
Janka si chce usporiadat na policku 4 anglicke a 3 slovenske knihy tak, aby boli zoradené najprv anglicke a potom slovenske knihy . Kolkymi sposobmi to moze urobit?
- 8 ludi
 8 ľudí sedí za okrúhlym stolom. Koľkými spôsobmi ich možno posadiť okolo stola?
8 ľudí sedí za okrúhlym stolom. Koľkými spôsobmi ich možno posadiť okolo stola? - Na hokejovom 2
 Na hokejovom turnaji sa stretne 16 družstiev. Koľkými spôsobmi môže byť udelená zlatá, strieborná a bronzová medaila?
Na hokejovom turnaji sa stretne 16 družstiev. Koľkými spôsobmi môže byť udelená zlatá, strieborná a bronzová medaila? - Polohy kníh
 Koľko je polôh k uloženiu troch knih na poličku?
Koľko je polôh k uloženiu troch knih na poličku? - Päť písmen
 Koľkými spôsobmi je možné usporiadať päť písmen?
Koľkými spôsobmi je možné usporiadať päť písmen? - V skupine
 V skupine je 11 žiakov, medzi nimi práve jeden Martin. Koľko je všetkých možností na rozdanie 4 rôznych kníh týmto žiakom, ak každý z nich má dostať najviac jednu a Martin práve jednu z týchto kníh".
V skupine je 11 žiakov, medzi nimi práve jeden Martin. Koľko je všetkých možností na rozdanie 4 rôznych kníh týmto žiakom, ak každý z nich má dostať najviac jednu a Martin práve jednu z týchto kníh".
- Telocvik
 Koľkými spôsobmi možno postaviť 20 žiakov do radu pri nástupe na telocvik?
Koľkými spôsobmi možno postaviť 20 žiakov do radu pri nástupe na telocvik? - Sedem 6
 Sedem spolužiačok chodí každý deň spolu na obed. Ak sa postavia do radu vždy v inom poradí, bude im stačiť školský rok, aby využili všetky možnosti?
Sedem spolužiačok chodí každý deň spolu na obed. Ak sa postavia do radu vždy v inom poradí, bude im stačiť školský rok, aby využili všetky možnosti? - Záhradník 2
 Záhradník má zasadiť 6 okrasných stromčekov. K dispozicií má 8 rozličných druhov stromov. Dva stromy A a B majú byť zasadené na ľavom okraji. Koľkými spôsobmi to môže záhradník spraviť, ak všetky zasadené stromčeky majú byť rôzne?
Záhradník má zasadiť 6 okrasných stromčekov. K dispozicií má 8 rozličných druhov stromov. Dva stromy A a B majú byť zasadené na ľavom okraji. Koľkými spôsobmi to môže záhradník spraviť, ak všetky zasadené stromčeky majú byť rôzne?
