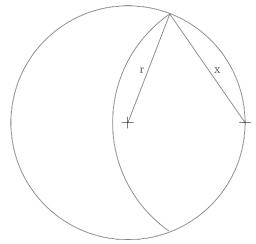
Koza - kruhy
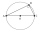
Aký je polomer kružnice, ktorá má stred na inej kružnici a prienik oboch kruhov je rovný polovici plochy prvej kružnice?
Táto úloha je matematickým vyjadrením úlohy z poľnohospodárstva. Sedliak má kruhový pozemok, na ktorom sa pasie koza. Pretože sedliak chce, aby jej tráva na pozemku vystačila na dva dni, uviaže ju ku kolu na okraji pozemku tak dlhým povrazom, aby za prvý deň spásla polovicu trávy. Druhý deň jej nechá k dispozícii celý pozemok, kde môžete spásť zvyšnú trávu.
Táto úloha je matematickým vyjadrením úlohy z poľnohospodárstva. Sedliak má kruhový pozemok, na ktorom sa pasie koza. Pretože sedliak chce, aby jej tráva na pozemku vystačila na dva dni, uviaže ju ku kolu na okraji pozemku tak dlhým povrazom, aby za prvý deň spásla polovicu trávy. Druhý deň jej nechá k dispozícii celý pozemok, kde môžete spásť zvyšnú trávu.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Najprirodzenejšou aplikáciou trigonometrie a goniometrických funkcií predstavuje výpočet trojuholníkov. Bežné aj menej bežné výpočty rôznych typov trojuholníkov ponúka naša trigonometrická kalkulačka trojuholníka. Slovo trigonometria pochádza z gréčtiny a doslovne znamená výpočet trojuholníka.
Najprirodzenejšou aplikáciou trigonometrie a goniometrických funkcií predstavuje výpočet trojuholníkov. Bežné aj menej bežné výpočty rôznych typov trojuholníkov ponúka naša trigonometrická kalkulačka trojuholníka. Slovo trigonometria pochádza z gréčtiny a doslovne znamená výpočet trojuholníka.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- rovnica
- planimetria
- kruh, kružnica
- obsah
- Euklidove vety
- kruhový výsek
- goniometria a trigonometria
- sínus
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- V pravouhlom 12
 V pravouhlom trojuholníku má prepona dĺžku 24cm. Päta výšky na preponu ju delí na dve časti v pomere 2:4. Akú veľkosť v cm má výška na preponu? Vypočítajte v centimetroch obvod tohto pravouhlého trojuholníka.
V pravouhlom trojuholníku má prepona dĺžku 24cm. Päta výšky na preponu ju delí na dve časti v pomere 2:4. Akú veľkosť v cm má výška na preponu? Vypočítajte v centimetroch obvod tohto pravouhlého trojuholníka. - Štvoruholník 10
 Daný je 4-uholník ABCD vpísaný do kružnice, pričom uhlopriečka AC je priemer kružnice. Vzdialenosť bodu B od priemeru je 15 cm, vzdialenosť bodu D od priemeru je 18 cm. Vypočítajte polomer kružnice a obvod 4-uholníka ABCD.
Daný je 4-uholník ABCD vpísaný do kružnice, pričom uhlopriečka AC je priemer kružnice. Vzdialenosť bodu B od priemeru je 15 cm, vzdialenosť bodu D od priemeru je 18 cm. Vypočítajte polomer kružnice a obvod 4-uholníka ABCD. - Euklidovka
 Poznáme v pravouhlom trojuholníku výšku na preponu vc = 4cm a preponu c= 19cm. Ako vypočitat časti strany - úseky na prepone c1, c2
Poznáme v pravouhlom trojuholníku výšku na preponu vc = 4cm a preponu c= 19cm. Ako vypočitat časti strany - úseky na prepone c1, c2 - Pomocou 5
 Pomocou Euklidovej vety zostrojte úsečku s dĺžkou √15.
Pomocou Euklidovej vety zostrojte úsečku s dĺžkou √15. - Bod dotyku
 Bod A má od kružnice s polomerom r = 4cm a stredom S vzdialenosť IA, kl = 10 cm. Vypočítajte: a) vzdialenosť bodu A od bodu dotyku T, ak je dotyčnica ku kružnici vedená z bodu A b) vzdialenosť dotykového bodu T od spojnice SA
Bod A má od kružnice s polomerom r = 4cm a stredom S vzdialenosť IA, kl = 10 cm. Vypočítajte: a) vzdialenosť bodu A od bodu dotyku T, ak je dotyčnica ku kružnici vedená z bodu A b) vzdialenosť dotykového bodu T od spojnice SA - MIT 1869
 Poznáte dĺžku častí 9 a 16, na ktoré preponu pravouhlého trojuholníka rozdelí kolmica spustená z jeho protiľahlého vrcholu. Úlohou je zistiť dĺžky strán trojuholníka a dĺžku úsečky x. Táto úloha bola súčasťou prijímacích skúšok na Massachusetts Institute
Poznáte dĺžku častí 9 a 16, na ktoré preponu pravouhlého trojuholníka rozdelí kolmica spustená z jeho protiľahlého vrcholu. Úlohou je zistiť dĺžky strán trojuholníka a dĺžku úsečky x. Táto úloha bola súčasťou prijímacích skúšok na Massachusetts Institute - Zostrojte 6
 Zostrojte štvorec, ktorý má obsah ako kosodĺžnik ABCD ak/AB/=5cm, /AD/=4cm a uhol |DAB|=30°
Zostrojte štvorec, ktorý má obsah ako kosodĺžnik ABCD ak/AB/=5cm, /AD/=4cm a uhol |DAB|=30° - Pravouhlý 26
 Pravouhlý trojuholník ABC má preponu c dlhú 9 cm a časť prepony cb= 3 cm. Aká dlhá je výška na stranu c?
Pravouhlý trojuholník ABC má preponu c dlhú 9 cm a časť prepony cb= 3 cm. Aká dlhá je výška na stranu c? - Vypočítaj 85
 Vypočítaj pravouhlý trojuholník ABC, odvesna b=43,5 cm prepona c=72,9 cm. Vypočítaj cb, a, ca, v?
Vypočítaj pravouhlý trojuholník ABC, odvesna b=43,5 cm prepona c=72,9 cm. Vypočítaj cb, a, ca, v? - Pre dĺžky
 Pre dĺžky odvesien pravouhlého trojuholníka ABC platí a: b = 2:3. Prepona má dĺžku 10 cm. Vypočítajte dĺžky odvesien toho trojuholníka.
Pre dĺžky odvesien pravouhlého trojuholníka ABC platí a: b = 2:3. Prepona má dĺžku 10 cm. Vypočítajte dĺžky odvesien toho trojuholníka. - Vypočítaj 50
 Vypočítaj zvyšné strany pravouhlého trojuholníka ak poznáš b= 4cm a vc = 2,4cm.
Vypočítaj zvyšné strany pravouhlého trojuholníka ak poznáš b= 4cm a vc = 2,4cm. - Trojuholníku 16223
 V pravouhlom trojuholníku ABC sú známe tieto prvky: a = 10 cm, vc = 9,23 cm. Vypočítajte o, R (polomer opísanej kružnice), r (polomer vpísanej kružnice).
V pravouhlom trojuholníku ABC sú známe tieto prvky: a = 10 cm, vc = 9,23 cm. Vypočítajte o, R (polomer opísanej kružnice), r (polomer vpísanej kružnice). - Starkého záhrada
 Starému otcovi ostal v záhrade voľný priestor v tvare pravouhlého trojuholníka s odvesnami dlhými 5 metrov a 12 metrov. Rozhodol sa ho rozdeliť na dve časti a to výškou na preponu. Na menšej časti vytvorí skalku, na väčšiu zaseje trávu. Koľko metrov štvor
Starému otcovi ostal v záhrade voľný priestor v tvare pravouhlého trojuholníka s odvesnami dlhými 5 metrov a 12 metrov. Rozhodol sa ho rozdeliť na dve časti a to výškou na preponu. Na menšej časti vytvorí skalku, na väčšiu zaseje trávu. Koľko metrov štvor - Štvorce
 Na dvoma stranami trojuholníka ABC sú zostrojené štvorce. Obsah štvorca nad stranou BC je 25 cm². Veľkosť výšky vc na stranu AB je 3 cm. Pata P výšky vc delí stranu AB v pomere 2:1. Strana AC je dlhšia ako strana BC. Vypočítajte v cm dĺžku strany AB. Vypo
Na dvoma stranami trojuholníka ABC sú zostrojené štvorce. Obsah štvorca nad stranou BC je 25 cm². Veľkosť výšky vc na stranu AB je 3 cm. Pata P výšky vc delí stranu AB v pomere 2:1. Strana AC je dlhšia ako strana BC. Vypočítajte v cm dĺžku strany AB. Vypo - Výpočet z ťažníc
 Pravouhlý trojuholník, uhol C je 90 stupňov. Poznám ťažnicu ta = 8 cm a ťažnicu tb = 12 cm. .. Ako spočítať dĺžku strán?
Pravouhlý trojuholník, uhol C je 90 stupňov. Poznám ťažnicu ta = 8 cm a ťažnicu tb = 12 cm. .. Ako spočítať dĺžku strán? - RR trojuholník
 Je daný rovnoramenný trojuholník ABC, kde AB = AC. Obvod je 64 cm a výška na základňu je 24 cm. Nájdite obsah tohto rovnoramenného trojuholníka
Je daný rovnoramenný trojuholník ABC, kde AB = AC. Obvod je 64 cm a výška na základňu je 24 cm. Nájdite obsah tohto rovnoramenného trojuholníka - PT strany
 Vypočítajte strany pravouhlého trojuholníka, ak je zadaná, že a + b = 17cm, polomer vpísanej kružnice ρ = 2cm.
Vypočítajte strany pravouhlého trojuholníka, ak je zadaná, že a + b = 17cm, polomer vpísanej kružnice ρ = 2cm.
