Auto
Podľa pravidiel cestnej premávky môžu stretávacie svetlá auta osvetľovať cestu do vzdialenosti maximálne 30 m. Kvôli kontrole dosahu stretávacích svetiel svojho auta zastavil Peter vo vzdialenosti 1,5 m od múru. Stretávacie svetlá sú na aute vo výške 60 cm. V akej výške na múre musí Peter nakresliť značku, aby podľa nej zistil, či jeho stretávacie svetlá svietia správne?
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Strýko
 Peter cestuje do domu svojho strýka 30 km od neho. Bicykluje 2/3 cesty, kým sa pri cykle nevyvinie mechanický problém a musí naň tlačiť po zvyšok cesty. Ak ide na bicykli o 10 km za hodinu rýchlejšie, než je jeho rýchlosť chôdze a cestu dokončí za 3 hodin
Peter cestuje do domu svojho strýka 30 km od neho. Bicykluje 2/3 cesty, kým sa pri cykle nevyvinie mechanický problém a musí naň tlačiť po zvyšok cesty. Ak ide na bicykli o 10 km za hodinu rýchlejšie, než je jeho rýchlosť chôdze a cestu dokončí za 3 hodin - Vlákno 2
 Vlákno žiarovky stretávacích svetiel auta má odpor 5 Ω. Aký veľký elektrický prúd ňou prechádza pri štandardnom napätí autobatérie 12 V?
Vlákno žiarovky stretávacích svetiel auta má odpor 5 Ω. Aký veľký elektrický prúd ňou prechádza pri štandardnom napätí autobatérie 12 V? - Paušál 2013
 Od roku 2013 plánuje vláda viac zdaniť živnostníkov. Namiesto 40% paušálnych výdavkov budú paušálne výdavky 40% hrubého príjmu maximálne 420 Eur. Vypočítajte koľko percent budú tvoriť paušálne výdavky podľa pravidiel v roku 2013 z hrubého príjmu 2437 Eur.
Od roku 2013 plánuje vláda viac zdaniť živnostníkov. Namiesto 40% paušálnych výdavkov budú paušálne výdavky 40% hrubého príjmu maximálne 420 Eur. Vypočítajte koľko percent budú tvoriť paušálne výdavky podľa pravidiel v roku 2013 z hrubého príjmu 2437 Eur. - Rebrík 11
 Rebrík má dĺžku 13m a jeho dolná časť je od steny vo vzdialenosti 5m. Do akej výšky siaha rebrík?
Rebrík má dĺžku 13m a jeho dolná časť je od steny vo vzdialenosti 5m. Do akej výšky siaha rebrík? - Vzdialenosti 3078
 Homogénny drevený trám dĺžky 6,00 m a hmotnosti 72,0 kg leží na vodorovnej plošine vysoko nad zemou a prečnieva o 1,80 m cez okraj plošiny a) Rozhodnite, či sa môže na visutý koniec trámu postaviť človek s hmotnosťou 60,0 kg. b) Určite maximálnu hmotnosť
Homogénny drevený trám dĺžky 6,00 m a hmotnosti 72,0 kg leží na vodorovnej plošine vysoko nad zemou a prečnieva o 1,80 m cez okraj plošiny a) Rozhodnite, či sa môže na visutý koniec trámu postaviť človek s hmotnosťou 60,0 kg. b) Určite maximálnu hmotnosť - Tri stĺpy
 Popri priamej ceste sú tri stĺpy vysoké 6 m v rovnakej vzdialenosti 10 m. Pod akým zorným uhlom vidí Vlado každý stĺp, ak je od prvého vo vzdialenosti 30 m a jeho oči sú vo výške 1,8 m?
Popri priamej ceste sú tri stĺpy vysoké 6 m v rovnakej vzdialenosti 10 m. Pod akým zorným uhlom vidí Vlado každý stĺp, ak je od prvého vo vzdialenosti 30 m a jeho oči sú vo výške 1,8 m? - Hojdačka
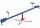 Dieťa vážiace 12 kg sedí na hojdačke vo vzdialenosti 130 cm od osi otáčania. Ako ďaleko od osi otáčania (od stredu hojdačky) si musí sadnúť jeho matka ak váži 57 kg a chceme, aby bola hojdačka v rovnováhe?
Dieťa vážiace 12 kg sedí na hojdačke vo vzdialenosti 130 cm od osi otáčania. Ako ďaleko od osi otáčania (od stredu hojdačky) si musí sadnúť jeho matka ak váži 57 kg a chceme, aby bola hojdačka v rovnováhe? - Vzdialenosti 9221
 Vo vetvách stromu sú dva leňochody. Jeden je vo vzdialenosti 2,5 m od kmeňa a druhý na druhej strane stromu vo vzdialenosti 4 m od kmeňa. Leňochi sa vydajú zoznámiť sa. Vypočítajte v akej vzdialenosti od kmeňa sa stretnú, pokiaľ lezú rovnakou konštantnou
Vo vetvách stromu sú dva leňochody. Jeden je vo vzdialenosti 2,5 m od kmeňa a druhý na druhej strane stromu vo vzdialenosti 4 m od kmeňa. Leňochi sa vydajú zoznámiť sa. Vypočítajte v akej vzdialenosti od kmeňa sa stretnú, pokiaľ lezú rovnakou konštantnou - Jama 4
 Táles je vzdialený 1 m od jamy. Oči má vo výške 150 cm nad zemou a pozerá do jamy s priemerom 120 cm podľa obrázka. Vypočítajte hĺbku jamy.
Táles je vzdialený 1 m od jamy. Oči má vo výške 150 cm nad zemou a pozerá do jamy s priemerom 120 cm podľa obrázka. Vypočítajte hĺbku jamy. - Bombardér
 Z akej vzdialenosti pred cieľom musí byť z lietadla letiaceho vo výške 1260 m zhodený náklad na padáku, ak sa znáša rýchlosťou 5,6 m/s a súčasne je unášaný v smere pohybu rýchlosťou 12 m/s. Aká je priama vzdialenosť lietadla od cieľa? (Najskôr si vypočíta
Z akej vzdialenosti pred cieľom musí byť z lietadla letiaceho vo výške 1260 m zhodený náklad na padáku, ak sa znáša rýchlosťou 5,6 m/s a súčasne je unášaný v smere pohybu rýchlosťou 12 m/s. Aká je priama vzdialenosť lietadla od cieľa? (Najskôr si vypočíta - V parku 4
 V parku je umiestený vo vzdialenosti 3m od chodníku postrekovač. Voda odstrelene do vzdialenosti max 5m. Maximálne akú dĺžku chodníka poleje?
V parku je umiestený vo vzdialenosti 3m od chodníku postrekovač. Voda odstrelene do vzdialenosti max 5m. Maximálne akú dĺžku chodníka poleje? - Bubon navijaka
 Pôvodne úplne vytočený bubon navijaka s priemerom 20cm a šírke 30cm na vyslobodzovacím aute, začal navíjať lano o sile 1cm od kraja ku kraju. Navijak sa zastavil po 80 otáčkach. Zostáva natočiť 3,54 lana (bez háku). Aké dlhé je celé lano?
Pôvodne úplne vytočený bubon navijaka s priemerom 20cm a šírke 30cm na vyslobodzovacím aute, začal navíjať lano o sile 1cm od kraja ku kraju. Navijak sa zastavil po 80 otáčkach. Zostáva natočiť 3,54 lana (bez háku). Aké dlhé je celé lano? - Kolesá traktora
 Predné koleso traktora má obvod 18 dm a zadný 60 dm. Na najspodnejšej mieste obidvoch kolies urobíme červenú značku. Traktor sa rozbehne. V akej vzdialenosti od štartu sa opäť obe značky objavia zhodne dole?
Predné koleso traktora má obvod 18 dm a zadný 60 dm. Na najspodnejšej mieste obidvoch kolies urobíme červenú značku. Traktor sa rozbehne. V akej vzdialenosti od štartu sa opäť obe značky objavia zhodne dole? - Vzdialený 39741
 Nikolka má z púte balónik na dva metre dlhom povrázku, ktorého koniec drží 60 cm nad zemou. Balónik sa vznáša šikmo od Nikolky a je od nej vodorovne vzdialený 145 cm. V akej výške je balónik od zeme?
Nikolka má z púte balónik na dva metre dlhom povrázku, ktorého koniec drží 60 cm nad zemou. Balónik sa vznáša šikmo od Nikolky a je od nej vodorovne vzdialený 145 cm. V akej výške je balónik od zeme? - Hojdačka
 Na hojdačke sú 2 dievčatá. Aneta s hmotnosťou 45kg a Simona s hmotnosťou 35kg. Ako ďaleko musí sedieť od stredu hojdačky Simona, tak aby boli v rovnováhe ak vieme, že Aneta sedí vo vzdialenosti 1,5 m? A ako ďaleko sedeli dievčatá od seba?
Na hojdačke sú 2 dievčatá. Aneta s hmotnosťou 45kg a Simona s hmotnosťou 35kg. Ako ďaleko musí sedieť od stredu hojdačky Simona, tak aby boli v rovnováhe ak vieme, že Aneta sedí vo vzdialenosti 1,5 m? A ako ďaleko sedeli dievčatá od seba? - Rebrík 15
 Rebrík dlhý 6,5 m je opretý o zvislú stenu. Jeho spodný koniec sa opiera o zem vo vzdialenosti 1,6 m od steny. Určte, do akej výšky dosahuje horný koniec rebríka a pod akým uhlom je rebrík opretý o stenu.
Rebrík dlhý 6,5 m je opretý o zvislú stenu. Jeho spodný koniec sa opiera o zem vo vzdialenosti 1,6 m od steny. Určte, do akej výšky dosahuje horný koniec rebríka a pod akým uhlom je rebrík opretý o stenu. - Vzdialenosťou 2927
 Zvuk sa vo vzduchu šíri rýchlosťou asi 330m/s. Zostav tabuľku závislosti medzi dobou (po jednej sekunde) a vzdialenosťou, ktorú zvuk za túto dobu prejde. Pri búrke potom ľahko zistíš, v akej vzdialenosti od nej si.
Zvuk sa vo vzduchu šíri rýchlosťou asi 330m/s. Zostav tabuľku závislosti medzi dobou (po jednej sekunde) a vzdialenosťou, ktorú zvuk za túto dobu prejde. Pri búrke potom ľahko zistíš, v akej vzdialenosti od nej si.
