Katka MO
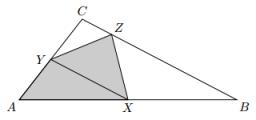
Katka narysovala trojuholník ABC. Stred strany AB si označila ako X a stred strany AC ako Y. Na strane BC chce nájsť taký bod Z, aby obsah štvoruholníka AXZY bol čo najväčší. Akú časť trojuholníka ABC môže maximálne zaberať štvoruholník AXZY?
Správna odpoveď:
Zobrazujem 2 komentáre:
Mo-1
Nápoveda. Určite, akú časť trojuholníka ABC zaberá trojuholník AXY.
Zo zadania vyplýva, že úsečka XY je strednou priečkou trojuholníka ABC, ktorá je rovnobežná so stranou BC. Jej dĺžka je teda polovičná vzhľadom k dĺžke strany BC a veľkosť výšky z A na XY je taktiež polovičná vzhľadom k veľkosti výšky z toho istého bodu na BC. To znamená, že trojuholník AXY má štvrtinový obsah vzhľadom na obsah trojuholníka ABC.
Teraz zvoľme bod Z na strane BC. Pretože úsečky BC a XY sú rovnobežné, je obsah trojuholníka XY Z, teda aj štvoruholníku XZY rovnaký pre akokoľvek zvolený bod Z. pretože vzdialenosť rovnobežiek BC a XY je rovnaká ako vzdialenosť XY od vrcholu A, majú trojuholníky AXY a XY Z tú istú veľkosť výšky na ich spoločnú stranu XY, a preto majú rovnaký obsah. Každý z týchto dvoch trojuholníkov zaberá štvrtinu trojuholníka ABC, štvoruholník AXZY preto zaberá polovicu trojuholníka ABC.
Zo zadania vyplýva, že úsečka XY je strednou priečkou trojuholníka ABC, ktorá je rovnobežná so stranou BC. Jej dĺžka je teda polovičná vzhľadom k dĺžke strany BC a veľkosť výšky z A na XY je taktiež polovičná vzhľadom k veľkosti výšky z toho istého bodu na BC. To znamená, že trojuholník AXY má štvrtinový obsah vzhľadom na obsah trojuholníka ABC.
Teraz zvoľme bod Z na strane BC. Pretože úsečky BC a XY sú rovnobežné, je obsah trojuholníka XY Z, teda aj štvoruholníku XZY rovnaký pre akokoľvek zvolený bod Z. pretože vzdialenosť rovnobežiek BC a XY je rovnaká ako vzdialenosť XY od vrcholu A, majú trojuholníky AXY a XY Z tú istú veľkosť výšky na ich spoločnú stranu XY, a preto majú rovnaký obsah. Každý z týchto dvoch trojuholníkov zaberá štvrtinu trojuholníka ABC, štvoruholník AXZY preto zaberá polovicu trojuholníka ABC.
Tipy na súvisiace online kalkulačky
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Opísaná kružnica
 Vypočítajte polomer kružnice opísaneho trojuholníku, ktorý má rozmery strán 8, 10 a 14cm.
Vypočítajte polomer kružnice opísaneho trojuholníku, ktorý má rozmery strán 8, 10 a 14cm. - Kruh odsek/úsek
 Kruh s priemerom 30 cm je preťať tetivou t = 16 cm. Vypočítajte obvod a obsah menšieho odseku.
Kruh s priemerom 30 cm je preťať tetivou t = 16 cm. Vypočítajte obvod a obsah menšieho odseku. - Polovica obĺžnika
 Vypočítajte obsah pravouhlého trojuholníka ABC s odvesnami a=15cm, b=1,7dm.
Vypočítajte obsah pravouhlého trojuholníka ABC s odvesnami a=15cm, b=1,7dm. - Výška, uhol a strana
 Vypočítajte obsah trojuholníka ABC, v ktorom poznáte stranu c=5 cm, uhol pri vrchole A= 70 stupňov a pomer úsekov, ktoré vytína výška na stranu c je 1:3.
Vypočítajte obsah trojuholníka ABC, v ktorom poznáte stranu c=5 cm, uhol pri vrchole A= 70 stupňov a pomer úsekov, ktoré vytína výška na stranu c je 1:3.
- Obvod 58
 Obvod štvobokého ihlava je 48 m a jeho výška ja 2,5m; koľko bude stáť plech na tento ihlan, keď 1m² stojí 1,5€; do plochy sa počíta aj 12% strata na spoje a záhyby.
Obvod štvobokého ihlava je 48 m a jeho výška ja 2,5m; koľko bude stáť plech na tento ihlan, keď 1m² stojí 1,5€; do plochy sa počíta aj 12% strata na spoje a záhyby. - Rovnoramenný trojuholník -VU
 Vypočítajte dĺžky strán v rovnoramennom trojuholníku, ak je dana výška (na základňu) Vc= 8,8cm a uhol pri zakladni alfa= 38°40`.
Vypočítajte dĺžky strán v rovnoramennom trojuholníku, ak je dana výška (na základňu) Vc= 8,8cm a uhol pri zakladni alfa= 38°40`. - Zastroj
 Zastroj rovnoramenný trojuholník ABY zo základňou AB dĺžky 5 cm a uhlom pri hlavnom vrchole veľkosti 50°. Zapíše postup konštrukcie.
Zastroj rovnoramenný trojuholník ABY zo základňou AB dĺžky 5 cm a uhlom pri hlavnom vrchole veľkosti 50°. Zapíše postup konštrukcie. - Tetiva - uhol
 Je daná kružnica k so stredom v bode S a polomerom 6 cm. Vypočítaj veľkosť stredového uhla, ktorý patí tetive dlhej 10 cm.
Je daná kružnica k so stredom v bode S a polomerom 6 cm. Vypočítaj veľkosť stredového uhla, ktorý patí tetive dlhej 10 cm. - Obsah 44
 Obsah pravouhlému trojuholníka ABC je 346 cm² a uhol pri vrchole A je 64°. Vypočítajte dĺžky odvesien a, b.
Obsah pravouhlému trojuholníka ABC je 346 cm² a uhol pri vrchole A je 64°. Vypočítajte dĺžky odvesien a, b.
- Ťažnice v PT
 V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku.
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku. - Daný je 9
 Daný je rovnoramenný trojuholník, ktorého základňa je 8cm a ramená majú dĺžku 15 cm. Vypočítaj obsah trojuholníka a polomer vpísanej a opísanej kružnice.
Daný je rovnoramenný trojuholník, ktorého základňa je 8cm a ramená majú dĺžku 15 cm. Vypočítaj obsah trojuholníka a polomer vpísanej a opísanej kružnice. - Trojuholníku 83150
 V trojuholníku ABC poznáte pomer dĺžok strán a:b:c=3:4:6. Vypočítajte veľkosti uhlov trojuholníka ABC.
V trojuholníku ABC poznáte pomer dĺžok strán a:b:c=3:4:6. Vypočítajte veľkosti uhlov trojuholníka ABC. - Rovnostraný trojuholník
 Vypočítaj stranu rovnostraného trojuholníka, ak jeho obvod je 132 cm.
Vypočítaj stranu rovnostraného trojuholníka, ak jeho obvod je 132 cm. - Rebrík 15
 Rebrík dlhý 6,5 m je opretý o zvislú stenu. Jeho spodný koniec sa opiera o zem vo vzdialenosti 1,6 m od steny. Určte, do akej výšky dosahuje horný koniec rebríka a pod akým uhlom je rebrík opretý o stenu.
Rebrík dlhý 6,5 m je opretý o zvislú stenu. Jeho spodný koniec sa opiera o zem vo vzdialenosti 1,6 m od steny. Určte, do akej výšky dosahuje horný koniec rebríka a pod akým uhlom je rebrík opretý o stenu.
- Deltoid 2
 Papierový šarkan má tvar deltoidu ABCD, v ktorom sú dve kratšie strany dlhé po 30 cm, dve dlhšie strany po 51 cm a kratšia uhlopriečka má dĺžku 48 cm. Určte veľkosti vnútorných uhlov daného deltoidu.
Papierový šarkan má tvar deltoidu ABCD, v ktorom sú dve kratšie strany dlhé po 30 cm, dve dlhšie strany po 51 cm a kratšia uhlopriečka má dĺžku 48 cm. Určte veľkosti vnútorných uhlov daného deltoidu. - Stúpanie cesty
 Na dopravnej značke, ktorá informuje o stúpaní cesty, je údaj 6,7 %. Určte uhol stúpania cesty. Aký výškový rozdiel prekonalo auto, ktoré prešlo po tejto ceste 2,8 km?
Na dopravnej značke, ktorá informuje o stúpaní cesty, je údaj 6,7 %. Určte uhol stúpania cesty. Aký výškový rozdiel prekonalo auto, ktoré prešlo po tejto ceste 2,8 km? - Značky
 Dopravné značky majú tvar rovnostranných trojuholníkov s dĺžkou strany 900 mm. Koľko eur stojí pozinkovaný plech na výrobu 50 kusov takýchto značiek, ak na odpad počítame s prídavkom 15% materiálu? Cena 1 meter štvorcový plechu je 6,5 eura.
Dopravné značky majú tvar rovnostranných trojuholníkov s dĺžkou strany 900 mm. Koľko eur stojí pozinkovaný plech na výrobu 50 kusov takýchto značiek, ak na odpad počítame s prídavkom 15% materiálu? Cena 1 meter štvorcový plechu je 6,5 eura.
