Pán Cuketa
Pán Cuketa mal obdĺžnikovú záhradu, ktorej obvod bol 28 metrov. Obsah celej záhrady vyplnili práve štyri štvorcové záhony, ktorých rozmery v metroch boli vyjadrené celými číslami. Určite aké rozmery mohla mať záhrada. Nájdite všetky možnosti a zapíšte n ako počet riešení.
Správna odpoveď:

Zobrazujem 5 komentárov:
Peter2
Ťahák: Uvedomte si, že štvorce nemusia mať rovnaké rozmery.
Možné riešenie. Obvod 28 = 2 · 14 metrov možno pomocou kladných celých čísel vyjadriť len niekoľko málo spôsobmi. Postupne všetky preberieme a zistíme, či možno zodpovedajúce záhon rozdeliť na štyri štvorce s celočíselnými rozmermi:
• 28 = 2 · (13 + 1), v takom prípade potrebujeme 13 štvorcov
• 28 = 2 · (12 + 2), v takom prípade potrebujeme najmenej 6 štvorcov
• 28 = 2 · (11 + 3), v takom prípade potrebujeme najmenej 6 štvorcov
• 28 = 2 · (10 + 4), v takom prípade stačí 4 štvorce
• 28 = 2 · (9 + 5), v takom prípade potrebujeme najmenej 6 štvorcov
• 28 = 2 · (8 + 6), v takom prípade stačí 4 štvorce
• 28 = 2 · (7 + 7), v takom prípade by bol záhon štvorcový a nie obdĺžnikový.
Záhrada mohla mať rozmery 10 × 4 alebo 8 × 6 metrov.
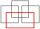
Iné riešenie. Uvažujme, ako možno zložiť jeden obdĺžnik zo štyroch štvorcov (všeobecne rôznych celočíselných rozmerov). To možno urobiť iba nasledujúcimi spôsobmi:
Ak veľkosť strany najmenšieho štvorca v metroch označíme a, potom obvod obdĺžnika v jednotlivých prípadoch je:
• 2 · (4a + a) = 10a, čo nie je presne 28 pre žiadne celé a.
• 2 · (5a + 2a) = 14a, čo je presne 28, práve keď a = 2; obdĺžnik má v takom prípade rozmery 10 × 4 metrov.
• 2 · (5a + 3a) = 16a, čo nie je presne 28 pre žiadne celé a.
• 2 · (4a + 3a) = 14a, čo je presne 28, práve keď a = 2; obdĺžnik má v takom prípade rozmery 8 × 6 metrov.
Možné riešenie. Obvod 28 = 2 · 14 metrov možno pomocou kladných celých čísel vyjadriť len niekoľko málo spôsobmi. Postupne všetky preberieme a zistíme, či možno zodpovedajúce záhon rozdeliť na štyri štvorce s celočíselnými rozmermi:
• 28 = 2 · (13 + 1), v takom prípade potrebujeme 13 štvorcov
• 28 = 2 · (12 + 2), v takom prípade potrebujeme najmenej 6 štvorcov
• 28 = 2 · (11 + 3), v takom prípade potrebujeme najmenej 6 štvorcov
• 28 = 2 · (10 + 4), v takom prípade stačí 4 štvorce
• 28 = 2 · (9 + 5), v takom prípade potrebujeme najmenej 6 štvorcov
• 28 = 2 · (8 + 6), v takom prípade stačí 4 štvorce
• 28 = 2 · (7 + 7), v takom prípade by bol záhon štvorcový a nie obdĺžnikový.
Záhrada mohla mať rozmery 10 × 4 alebo 8 × 6 metrov.
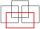
Iné riešenie. Uvažujme, ako možno zložiť jeden obdĺžnik zo štyroch štvorcov (všeobecne rôznych celočíselných rozmerov). To možno urobiť iba nasledujúcimi spôsobmi:
Ak veľkosť strany najmenšieho štvorca v metroch označíme a, potom obvod obdĺžnika v jednotlivých prípadoch je:
• 2 · (4a + a) = 10a, čo nie je presne 28 pre žiadne celé a.
• 2 · (5a + 2a) = 14a, čo je presne 28, práve keď a = 2; obdĺžnik má v takom prípade rozmery 10 × 4 metrov.
• 2 · (5a + 3a) = 16a, čo nie je presne 28 pre žiadne celé a.
• 2 · (4a + 3a) = 14a, čo je presne 28, práve keď a = 2; obdĺžnik má v takom prípade rozmery 8 × 6 metrov.
Ivo
Ahoj Hana; no v prípade MO sa nejedná o ľahké príklady, ktorým musí rozumieť každý. Ale tým že toto riešenie (vlastne dve) budeš študovať možno aj týždne, sa niečo nové naučíš...
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Téma:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Záhrada
 Obvod obdĺžnikovej záhrady hruškových je 98 metrov. Šírka záhrady je práve o 60% kratšia ako jej dĺžka. Určite v metroch rozmery obdĺžnikové záhrady. Určite v metroch štvorcových výmeru záhrady.
Obvod obdĺžnikovej záhrady hruškových je 98 metrov. Šírka záhrady je práve o 60% kratšia ako jej dĺžka. Určite v metroch rozmery obdĺžnikové záhrady. Určite v metroch štvorcových výmeru záhrady. - Pán Marek
 Pán Marek si chce v záhrade vybudovať kruhové jazierko. Jeho prianím je, aby obvod jazierka v metroch aj rozloha v metroch štvorcových boli vyjadrené rovnakými číslami. Aký polomer má mať jazierko?
Pán Marek si chce v záhrade vybudovať kruhové jazierko. Jeho prianím je, aby obvod jazierka v metroch aj rozloha v metroch štvorcových boli vyjadrené rovnakými číslami. Aký polomer má mať jazierko? - Vystrihol som obdĺžniky
 Vystrihol som si dva obdĺžniky s obsahmi 54 cm², 90 cm². Ich strany sú vyjadrene celými číslami v centimetroch. Ak tieto obdĺžniky priložím k sebe, dostanem obdĺžnik s obsahom 144 cm². Aké rozmery môže mat tento veľký obdĺžnik? Napíš všetky možnosti. Svoj
Vystrihol som si dva obdĺžniky s obsahmi 54 cm², 90 cm². Ich strany sú vyjadrene celými číslami v centimetroch. Ak tieto obdĺžniky priložím k sebe, dostanem obdĺžnik s obsahom 144 cm². Aké rozmery môže mat tento veľký obdĺžnik? Napíš všetky možnosti. Svoj - Obvod obdĺžnika
 Obvod obdĺžnika je 22 cm a obsah 30 cm². Určte jeho rozmery, ak sú dĺžky strán obdĺžnika v centimetroch vyjadrené celými číslami.
Obvod obdĺžnika je 22 cm a obsah 30 cm². Určte jeho rozmery, ak sú dĺžky strán obdĺžnika v centimetroch vyjadrené celými číslami. - Z6–I–2
 Pán Kockorád vlastnil záhradu obdĺžnikového tvaru, na ktorej postupne dláždil chodníky z jednej strany na druhú. Chodníky boli rovnako široké, križovali sa na dvoch miestach a už vydláždená plocha sa pri ďalšom dláždení preskakovala. Keď pán Kockorád vydl
Pán Kockorád vlastnil záhradu obdĺžnikového tvaru, na ktorej postupne dláždil chodníky z jednej strany na druhú. Chodníky boli rovnako široké, križovali sa na dvoch miestach a už vydláždená plocha sa pri ďalšom dláždení preskakovala. Keď pán Kockorád vydl - Rozdeľte 3
 Rozdeľte štvorcovú záhradu s obvodom 124 m na dve obdĺžnikové záhrady tak, aby plot jednej záhrady bol o 10 m dlhší ako plot druhej záhrady. Aké rozmery budú mať tieto obdĺžnikové záhrady?
Rozdeľte štvorcovú záhradu s obvodom 124 m na dve obdĺžnikové záhrady tak, aby plot jednej záhrady bol o 10 m dlhší ako plot druhej záhrady. Aké rozmery budú mať tieto obdĺžnikové záhrady? - Vláčik
 Čísla 1,2,3,4,5,6,7,8 a 9 cestovala vlakom. Vlak mal tri vagóny a v každom sa viezla práve tri čísla. Číslo 1 sa viezlo v prvom vagóne a v poslednom vagóne boli všetky čísla nepárne. Sprievodcovia cestou spočítal súčet čísel v prvom, druhom i posledným va
Čísla 1,2,3,4,5,6,7,8 a 9 cestovala vlakom. Vlak mal tri vagóny a v každom sa viezla práve tri čísla. Číslo 1 sa viezlo v prvom vagóne a v poslednom vagóne boli všetky čísla nepárne. Sprievodcovia cestou spočítal súčet čísel v prvom, druhom i posledným va - 144 krokov
 Aby sme obišli záhradu musíme urobiť 144 krokov. Na šírku o 8 krokov menej ako na dĺžku. Jeden krok je dlhý 5 decimetrov. Aké sú rozmery záhrady? Aký je jej obvod a obsah?
Aby sme obišli záhradu musíme urobiť 144 krokov. Na šírku o 8 krokov menej ako na dĺžku. Jeden krok je dlhý 5 decimetrov. Aké sú rozmery záhrady? Aký je jej obvod a obsah? - Máme vytvoriť
 Máme vytvoriť políčko v tvare obdĺžnika s rozlohou 288 m² (štvorcových), tak aby strany boli celé čísla. Aké sú všetky rozmery obdĺžnikového políčka, ktoré môžeme vytvoriť? Koľko je riešení.
Máme vytvoriť políčko v tvare obdĺžnika s rozlohou 288 m² (štvorcových), tak aby strany boli celé čísla. Aké sú všetky rozmery obdĺžnikového políčka, ktoré môžeme vytvoriť? Koľko je riešení. - Záhrada
 Chceme ohradiť obdĺžnikovú záhradu, ktorej pomer dĺžky a šírky je 2 : 1 a ktorej polovica obvodu hraničí s cestou. Cesta ohradenia pozdĺž cesty stojí 7 eur za meter ostatné ohradenie len 3 eurá za meter. Koľko árov má záhrada, ak jej ohradenie stojí 363 e
Chceme ohradiť obdĺžnikovú záhradu, ktorej pomer dĺžky a šírky je 2 : 1 a ktorej polovica obvodu hraničí s cestou. Cesta ohradenia pozdĺž cesty stojí 7 eur za meter ostatné ohradenie len 3 eurá za meter. Koľko árov má záhrada, ak jej ohradenie stojí 363 e - Záhrada
 Záhrada má tvar štvorca o=124m, urob dve obdĺžnikové záhrady aby jedna záhrada mala obvod o 10m viac ako druhá. Aké rozmery budú mať záhrady?
Záhrada má tvar štvorca o=124m, urob dve obdĺžnikové záhrady aby jedna záhrada mala obvod o 10m viac ako druhá. Aké rozmery budú mať záhrady? - Záhrada 30
 Záhrada má tvar pravouhlého lichobežníka, ktorého základne majú rozmery 60 m a 30 m a kolmé rameno 40 m. Majiteľ túto záhradu vymenil za rovnobežníkovú, ktorej obsah je 7/9 obsahu lichobežníkovej záhrady. Akú výmeru v ároch má nová záhrada?
Záhrada má tvar pravouhlého lichobežníka, ktorého základne majú rozmery 60 m a 30 m a kolmé rameno 40 m. Majiteľ túto záhradu vymenil za rovnobežníkovú, ktorej obsah je 7/9 obsahu lichobežníkovej záhrady. Akú výmeru v ároch má nová záhrada? - Zaujímavá vlastnosť
 Pozemok tvaru obdĺžnika má tú zaujímavú vlastnosť, že obvod v metroch a obsah v metroch štvorcových sú rovnaké čísla. Aké rozmery môže obdĺžnik mať?
Pozemok tvaru obdĺžnika má tú zaujímavú vlastnosť, že obvod v metroch a obsah v metroch štvorcových sú rovnaké čísla. Aké rozmery môže obdĺžnik mať? - Obdĺžnik
 Záhrada má tvar obdĺžnika a má obvod dĺžky 130m a obsah 800,25m². Vypočitajte rozmery záhrady.
Záhrada má tvar obdĺžnika a má obvod dĺžky 130m a obsah 800,25m². Vypočitajte rozmery záhrady. - Záhrada 38
 Záhrada tvaru štvorca má z troch strán živý plot. Jeho dĺžka je 36 metrov. Aký je obsah záhrady v m²?
Záhrada tvaru štvorca má z troch strán živý plot. Jeho dĺžka je 36 metrov. Aký je obsah záhrady v m²? - Obdĺžnika 4389
 Strýček Ferda mal dve záhrady: mrkvová mala tvar štvorca, jahodová mala tvar obdĺžnika. Pritom šírka jahodovej záhrady bola trikrát menšia ako šírka mrkvovej záhrady a dĺžka jahodovej záhrady bola o 8 metrov dlhšia ako dĺžka mrkvovej záhrady. Keď strýko z
Strýček Ferda mal dve záhrady: mrkvová mala tvar štvorca, jahodová mala tvar obdĺžnika. Pritom šírka jahodovej záhrady bola trikrát menšia ako šírka mrkvovej záhrady a dĺžka jahodovej záhrady bola o 8 metrov dlhšia ako dĺžka mrkvovej záhrady. Keď strýko z - Vyjadrite 6140
 Do obchodu dostali celkom 666 párov detských, pánskych, dámskych topánok. Pánskych bolo 2,5-krát menej ako detských, pritom detských bolo 1,4-krát viac ako dámskych. Vyjadrite celými číslami, v akom pomere bol počet párov detskej, pánskej a dámskej obuvi.
Do obchodu dostali celkom 666 párov detských, pánskych, dámskych topánok. Pánskych bolo 2,5-krát menej ako detských, pritom detských bolo 1,4-krát viac ako dámskych. Vyjadrite celými číslami, v akom pomere bol počet párov detskej, pánskej a dámskej obuvi.
