Tetiva
V kružnici s polomerom r=70 cm je tetiva 10 × dlhšia ako jej vzdialenosť od stredu. Aká je dĺžka tetivy?
Správna odpoveď:
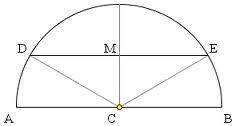
Zobrazujem 4 komentáre:
Žiak
Mohol by mi niekto prosim vysvetlit ako prisli na to riesenie? Ja som mala iny sposob tomu som rozumela ale mi to nevyslo a tomuto tu nechapem. Dakujem
Žiak
Prepacte za asi blbu otazku ale ako z toho vyrazu zo 4. riadka po uprave dostanem to pod nim???
Tipy na súvisiace online kalkulačky
Chcete premeniť jednotku dĺžky?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- vyjadrenie neznámej zo vzorca
- aritmetika
- odmocnina
- druhá mocnina
- planimetria
- Pytagorova veta
- pravouhlý trojuholník
- kruh, kružnica
- trojuholník
- tetiva
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Tetiva
 V kružnici s polomerom 10 cm je 12 cm dlhá tetiva. Vypočítaj vzdialenosť tetivy od stredu kružnice.
V kružnici s polomerom 10 cm je 12 cm dlhá tetiva. Vypočítaj vzdialenosť tetivy od stredu kružnice. - Tetiva
 V kružnici k (S; 6cm) vypočítajte vzdialenosť tetivy t od stredu kružnice S, ak dĺžka tetivy je t= 10cm.
V kružnici k (S; 6cm) vypočítajte vzdialenosť tetivy t od stredu kružnice S, ak dĺžka tetivy je t= 10cm. - Tetiva 2
 Bod A má od stredu kružnice s polomerom r = 5 cm vzdialenosť 13 cm. Vypočítajte dĺžku tetivy spájajúca body dotyku T1 a T2 dotyčníc vedených z bodu A ku kružnici k.
Bod A má od stredu kružnice s polomerom r = 5 cm vzdialenosť 13 cm. Vypočítajte dĺžku tetivy spájajúca body dotyku T1 a T2 dotyčníc vedených z bodu A ku kružnici k. - V kružnici 3
 V kružnici k s polomerom 13 cm je tetiva AB. Stred C tetivy AB je od stredu S kruž nice vzdialený 5 cm. Aká dlhá je tetiva AB?
V kružnici k s polomerom 13 cm je tetiva AB. Stred C tetivy AB je od stredu S kruž nice vzdialený 5 cm. Aká dlhá je tetiva AB?
- Tetiva 4
 Potrebujem vypočítať obvod kruhu, keď poznám dĺžku tetivy t=22 cm a vzdialenosť od stredu d=29 cm tetivy ku kružnici.
Potrebujem vypočítať obvod kruhu, keď poznám dĺžku tetivy t=22 cm a vzdialenosť od stredu d=29 cm tetivy ku kružnici. - Tetiva 5
 Vypočítajte dĺžku tetivy kružnice s polomerom r = 10 cm, ktorej dĺžka sa rovná jej vzdialenosti od stredu kružnice.
Vypočítajte dĺžku tetivy kružnice s polomerom r = 10 cm, ktorej dĺžka sa rovná jej vzdialenosti od stredu kružnice. - Medzikružie 6
 Na obrázku sú 2 sústredné kružnice. Tetiva väčšej kružnice s dĺžkou 10 cm je dotyčnicou menšej kružnice. Aký obsah má medzikružie?
Na obrázku sú 2 sústredné kružnice. Tetiva väčšej kružnice s dĺžkou 10 cm je dotyčnicou menšej kružnice. Aký obsah má medzikružie? - Dve tetivy
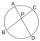 V kružnici sú vedené dve tetivy dlhé 30 a 34 cm. Kratšia z nich je od stredu dvakrát ďalej než dlhšia. Urči polomer kružnice.
V kružnici sú vedené dve tetivy dlhé 30 a 34 cm. Kratšia z nich je od stredu dvakrát ďalej než dlhšia. Urči polomer kružnice. - Tetiva
 Vypočítaj dĺžku tetivy, ktorej vzdialenosť od stredu S kružnice k (S, 8 cm) sa rovná 7 cm.
Vypočítaj dĺžku tetivy, ktorej vzdialenosť od stredu S kružnice k (S, 8 cm) sa rovná 7 cm.
- Vzdialenosť 79144
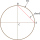 Polomer kružnice r=8,9 cm, tetiva AB tejto kružnice má dĺžku 16 cm. Vypočítaj vzdialenosť tetivy AB od stredu kružnice.
Polomer kružnice r=8,9 cm, tetiva AB tejto kružnice má dĺžku 16 cm. Vypočítaj vzdialenosť tetivy AB od stredu kružnice. - Tetivy
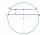 V kružnici s polomerom 8,5 cm sú zostrojené dve rovnobežné tetivy, ktorých dĺžky sú 9 cm a 12 cm. Vypočítajte vzdialenosť tetív v kružnici.
V kružnici s polomerom 8,5 cm sú zostrojené dve rovnobežné tetivy, ktorých dĺžky sú 9 cm a 12 cm. Vypočítajte vzdialenosť tetív v kružnici. - Kružnice
 V kružnici s polomerom 7,5 cm sú zostrojené 2 rovnobežné tetivy, ktorých dĺžky sú 9 cm a 12 cm. Vypočítajte vzdialenosť týchto tetív (ak sú možné dve riešenia napíšte obe).
V kružnici s polomerom 7,5 cm sú zostrojené 2 rovnobežné tetivy, ktorých dĺžky sú 9 cm a 12 cm. Vypočítajte vzdialenosť týchto tetív (ak sú možné dve riešenia napíšte obe). - Tetivka
 Vypočítaj vzdialenosť tetivy dlhej 19 cm od stredu kružnice s priemerom 28 cm.
Vypočítaj vzdialenosť tetivy dlhej 19 cm od stredu kružnice s priemerom 28 cm. - Tetiva 5
 Vypočítaj dĺžku tetivy kružnice, ktorá je vzdialená od stredu kružnice 2,5 cm. Polomer je 6,5 cm.
Vypočítaj dĺžku tetivy kružnice, ktorá je vzdialená od stredu kružnice 2,5 cm. Polomer je 6,5 cm.
- Dve tetivy 4
 V kružnici s r=26 cm sú narysované 2 rovnobežné tetivy . Jedna tetiva má dĺžku t1=48 cm a druhá má dĺžku t2=20cm, pričom stred leží medzi nimi. Vypočítaj vzdialenosť dvoch tetív.
V kružnici s r=26 cm sú narysované 2 rovnobežné tetivy . Jedna tetiva má dĺžku t1=48 cm a druhá má dĺžku t2=20cm, pričom stred leží medzi nimi. Vypočítaj vzdialenosť dvoch tetív. - Tetiva
 Určite polomer kružnice v ktorej tetiva vzdialená 8 cm od stredu kružnice je o 11 cm dlhšia ako polomer kružnice.
Určite polomer kružnice v ktorej tetiva vzdialená 8 cm od stredu kružnice je o 11 cm dlhšia ako polomer kružnice. - V kružnici 2
 V kružnici s priemerom 70 cm sú narysované dve rovnobežné tetivy tak, že stred kružnice leží medzi tetivami. Vypočítaj vzdialenosť týchto tetív, ak jedna z nich má dĺžku 42 cm a druhá 56 cm.
V kružnici s priemerom 70 cm sú narysované dve rovnobežné tetivy tak, že stred kružnice leží medzi tetivami. Vypočítaj vzdialenosť týchto tetív, ak jedna z nich má dĺžku 42 cm a druhá 56 cm.
