Distribučná funkcia
X 2 3 4
p 0,3 0,35 0,35
Pre údaje v tejto tabuľke mám vypočítať distribučnú funkciu F(x) a ďalej p(2,5 < ξ < 3,25), p(2,8 < ξ) a p(3,25 > ξ)
p 0,3 0,35 0,35
Pre údaje v tejto tabuľke mám vypočítať distribučnú funkciu F(x) a ďalej p(2,5 < ξ < 3,25), p(2,8 < ξ) a p(3,25 > ξ)
Správna odpoveď:
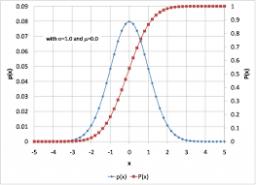
Tipy na súvisiace online kalkulačky
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Pravdepodobnosti 80837
 Strelec má tri náboje. Rozhodol sa, že bude strieľať na terč, kým sa prvýkrát netrafí. Pravdepodobnosť zásahu je pri každom výstrele 0,6. Náhodná veličina X udáva počet vystrelených nábojov. a) Napíšte rozdelenie pravdepodobnosti náhodnej veličiny X a jej
Strelec má tri náboje. Rozhodol sa, že bude strieľať na terč, kým sa prvýkrát netrafí. Pravdepodobnosť zásahu je pri každom výstrele 0,6. Náhodná veličina X udáva počet vystrelených nábojov. a) Napíšte rozdelenie pravdepodobnosti náhodnej veličiny X a jej - Nech náhodná
 Nech náhodná veličina ξ predstavuje počet spokojných zákazníkov. Pravdepodobnosť spokojného zákazníka pri každom zo štyroch zákazníkov je 7/10. Určte: a) rozdelenie pravdepodobností, distribučnú funkciu F(x) a P(-0,5 < ξ < 3,1) b) rozptyl náhodnej v
Nech náhodná veličina ξ predstavuje počet spokojných zákazníkov. Pravdepodobnosť spokojného zákazníka pri každom zo štyroch zákazníkov je 7/10. Určte: a) rozdelenie pravdepodobností, distribučnú funkciu F(x) a P(-0,5 < ξ < 3,1) b) rozptyl náhodnej v - Vo voľbách 2
 Vo voľbách stranu Z volilo 2400000 voličov z celkového počtu 6000000 voličov. Vyberme náhodne troch voličov a uvažujme náhodnú veličinu ξ={počet voličov strany Z vo výbere z troch voličov}. Určte a) rozdelenie pravdepodobností, distribučnú funkciu F(x) a
Vo voľbách stranu Z volilo 2400000 voličov z celkového počtu 6000000 voličov. Vyberme náhodne troch voličov a uvažujme náhodnú veličinu ξ={počet voličov strany Z vo výbere z troch voličov}. Určte a) rozdelenie pravdepodobností, distribučnú funkciu F(x) a - Pravdepodobnosť 55293
 Náhodná veličina, ktorá modeluje dobu medzi 2 telef. Hovory má exponenciálne rozdelenie s hustotou f(x)=10exp (-10x), x je väčšia ako 0. Spočítaj jej distribučnú funkciu a pravdepodobnosť, že doba medzi hovormi neprekročí 5 sekúnd, doba medzi hovormi prek
Náhodná veličina, ktorá modeluje dobu medzi 2 telef. Hovory má exponenciálne rozdelenie s hustotou f(x)=10exp (-10x), x je väčšia ako 0. Spočítaj jej distribučnú funkciu a pravdepodobnosť, že doba medzi hovormi neprekročí 5 sekúnd, doba medzi hovormi prek
- Vo voľbách
 Vo voľbách stranu Z volilo 2400000 voličov z celkového počtu 6000000 voličov. Vyberme náhodne troch voličov a uvažujme náhodnú veličinu ξ={počet voličov strany Z vo výbere z troch voličov}. Určte a) rozdelenie pravdepodobností, distribučnú funkciu F(x) a
Vo voľbách stranu Z volilo 2400000 voličov z celkového počtu 6000000 voličov. Vyberme náhodne troch voličov a uvažujme náhodnú veličinu ξ={počet voličov strany Z vo výbere z troch voličov}. Určte a) rozdelenie pravdepodobností, distribučnú funkciu F(x) a - Vypočítajte 38
 Vypočítajte dĺžku ramien a obsah rovnoramenného lichobežníka, ak poznáte nasledujúce parametre: o = 20 cm a = 10 cm, c = 4 cm v = 2 cm
Vypočítajte dĺžku ramien a obsah rovnoramenného lichobežníka, ak poznáte nasledujúce parametre: o = 20 cm a = 10 cm, c = 4 cm v = 2 cm - Desatinnom 82325
 Čísla uvedené v tabuľke hodnôt miest zapíšte v desatinnom tvare. Stovky desiatok. Jedničky. Desiatky. 6. 1. 5. 4 8. 3. 2. 5 7. 9. 0. 3 1. 0. 3. 1 4. 8. 0. 7
Čísla uvedené v tabuľke hodnôt miest zapíšte v desatinnom tvare. Stovky desiatok. Jedničky. Desiatky. 6. 1. 5. 4 8. 3. 2. 5 7. 9. 0. 3 1. 0. 3. 1 4. 8. 0. 7 - Ušetrenie
 V tabuľke sú uvedené údaje, ktoré rodina minula minulý rok na vianočné darčeky. Tento rok plánujú znížiť výdavky o 20% oproti minulému roku. Koľko eur ušetrí rodina na darčekoch oproti minulému roku? Knihy 50,50 Kozmetika 35,00 Hračky 25,50 Oblečenie 39,0
V tabuľke sú uvedené údaje, ktoré rodina minula minulý rok na vianočné darčeky. Tento rok plánujú znížiť výdavky o 20% oproti minulému roku. Koľko eur ušetrí rodina na darčekoch oproti minulému roku? Knihy 50,50 Kozmetika 35,00 Hračky 25,50 Oblečenie 39,0 - Drahé kovy
 V rokoch 2006-2009 sa hodnota drahých kovov rýchlo zmenila. Údaje v nasledujúcej tabuľke predstavujú celkovú mieru návratnosti (v percentách) platiny, zlata, striebra od roku 2006 do roku 2009: Rok Platinum Gold Silver 2009 62,7 25,0 56,8 2008 -41,3 4,3 -
V rokoch 2006-2009 sa hodnota drahých kovov rýchlo zmenila. Údaje v nasledujúcej tabuľke predstavujú celkovú mieru návratnosti (v percentách) platiny, zlata, striebra od roku 2006 do roku 2009: Rok Platinum Gold Silver 2009 62,7 25,0 56,8 2008 -41,3 4,3 -
- Máme 4,5
 Máme 4,5 litrov sirupu, a 80% tvori šťava. Koľko litrov bolo šťavy?
Máme 4,5 litrov sirupu, a 80% tvori šťava. Koľko litrov bolo šťavy? - Rozviňte
 Rozviňte funkciu f(z) do Laurentovho radu v bode z0 pre dané medzikružie f(z)=1/((z-2)*(z-3)) a) z0=2, 03
Rozviňte funkciu f(z) do Laurentovho radu v bode z0 pre dané medzikružie f(z)=1/((z-2)*(z-3)) a) z0=2, 03 - Vyriešených 32751
 Tabuľka je uvedená: dní sťažnosti 0-4 2 5-9 4 10-14 8 15-19 6 20-24 4 25-29 3 30-34 3 1,1 Aké percento sťažností bolo vyriešených do 2 týždňov? 1,2 vypočítať priemerný počet dní na vyriešenie týchto sťažností. 1,3 vypočítať modálny počet dní pre vyriešeni
Tabuľka je uvedená: dní sťažnosti 0-4 2 5-9 4 10-14 8 15-19 6 20-24 4 25-29 3 30-34 3 1,1 Aké percento sťažností bolo vyriešených do 2 týždňov? 1,2 vypočítať priemerný počet dní na vyriešenie týchto sťažností. 1,3 vypočítať modálny počet dní pre vyriešeni - Nákup 6
 V obchode Janko kúpil 300g šunky,5 rožkov, 1,5kg paradajok a 2l mlieka. Jednotkové ceny sú uvedené v tabuľke - šunka 6,50e/kg, rožky 0,06e/ks paradajky 3,4e/kg mlieko 0,95e/l. Kolko zaplatil Janko za nákup?
V obchode Janko kúpil 300g šunky,5 rožkov, 1,5kg paradajok a 2l mlieka. Jednotkové ceny sú uvedené v tabuľke - šunka 6,50e/kg, rožky 0,06e/ks paradajky 3,4e/kg mlieko 0,95e/l. Kolko zaplatil Janko za nákup? - Uhol BSA
 Je daná kružnica k (S; r) a bod A, ktorý leží na tejto kružnici. Na obvode leží aj bod B, pre ktorý platí, že je v jednom smere päťkrát ďalej od bodu A, než v opačnom smere (po obvode kružnice). Určte veľkosť konvexného uhla BSA.
Je daná kružnica k (S; r) a bod A, ktorý leží na tejto kružnici. Na obvode leží aj bod B, pre ktorý platí, že je v jednom smere päťkrát ďalej od bodu A, než v opačnom smere (po obvode kružnice). Určte veľkosť konvexného uhla BSA.
- Trojuholníku 81883
 Dobrý deň, mám problém vypočítať výšku na stranu z vo všeobecnom trojuholníku XYZ, kde z = 4 cm, x = 1,5 cm a y = 3,7 cm. Bolo zadané v 8. triede pri preberaní Pytagorovej vety. Ďakujem.
Dobrý deň, mám problém vypočítať výšku na stranu z vo všeobecnom trojuholníku XYZ, kde z = 4 cm, x = 1,5 cm a y = 3,7 cm. Bolo zadané v 8. triede pri preberaní Pytagorovej vety. Ďakujem. - Smerodajná odchýlka
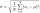 Nájdite smerodajnú (štandardnú) odchýlku pre množinu údajov (zoskupené údaje): Vek (v rokoch) Počet osôb 0-10 15 10-20 15 20-30 23 30-40 22 40-50 25 50-60 10 60-70 5 70-80 10
Nájdite smerodajnú (štandardnú) odchýlku pre množinu údajov (zoskupené údaje): Vek (v rokoch) Počet osôb 0-10 15 10-20 15 20-30 23 30-40 22 40-50 25 50-60 10 60-70 5 70-80 10 - Spoločnosťami 13451
 V tabuľke nižšie sú uvedené ceny akcií, zisk na akciu a dividendy na akciu pre tri spoločnosti za posledný rok: Deere & Co. Cena 65,70 USD zisk na akciu 4,40 USD Dividendy na akciu 1,16 USD Cena Google 528,33 USD zisk na akciu 27,72 USD Dividendy na akciu
V tabuľke nižšie sú uvedené ceny akcií, zisk na akciu a dividendy na akciu pre tri spoločnosti za posledný rok: Deere & Co. Cena 65,70 USD zisk na akciu 4,40 USD Dividendy na akciu 1,16 USD Cena Google 528,33 USD zisk na akciu 27,72 USD Dividendy na akciu
