Prvý a tretí člen
Určte prvý a tretí člen GP, ak q=-8,a a2+a5=8176
Správna odpoveď:

Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Geometrická
 Určte tretí člen a kvocient GP, ak a2=-3, a1+a2=-2,5
Určte tretí člen a kvocient GP, ak a2=-3, a1+a2=-2,5 - Geometrická
 Určte tretí a štvrtý člen GP, ak q=-0,6 a a1+a2=-0,2
Určte tretí a štvrtý člen GP, ak q=-0,6 a a1+a2=-0,2 - Kvocientík
 Určte kvocient a prvý člen GP, ak a3=0,39, a a1+a2=0,39.
Určte kvocient a prvý člen GP, ak a3=0,39, a a1+a2=0,39. - Kvocient a tretí člen
 Určte tretí člen GP, ak a1+a2=36 a a1+a3=90. Vypočítajte aj kvocient.
Určte tretí člen GP, ak a1+a2=36 a a1+a3=90. Vypočítajte aj kvocient. - Kvocientík 3
 Určte kvocient a prvý člen GP, ak a3=0,52, a a1+a2=0,39.
Určte kvocient a prvý člen GP, ak a3=0,52, a a1+a2=0,39. - Štvrtý člen GP
 Určte štvrtý člen GP, ak q=4 a a1+a3=5,44
Určte štvrtý člen GP, ak q=4 a a1+a3=5,44 - Kvocient a druhý člen
 Určte kvocient a druhý člen GP, ak a3=-5, a2+a3=-7
Určte kvocient a druhý člen GP, ak a3=-5, a2+a3=-7 - Kvocient a šiesty člen
 Určte kvocient a šiesty člen GP, ak a1=420, a1+a2=630.
Určte kvocient a šiesty člen GP, ak a1=420, a1+a2=630. - Kvocient či koeficient
 Určte kvocient a druhý člen GP, ak a3=10, a1+a2=-1,6 a1-a2=2,4.
Určte kvocient a druhý člen GP, ak a3=10, a1+a2=-1,6 a1-a2=2,4. - Člen a kvocient
 Určte druhý člen a kvocient GP, ak a3=48,6 a1+a2=6
Určte druhý člen a kvocient GP, ak a3=48,6 a1+a2=6 - Geometrická 6
 Určte tretí, štvrtý a piaty člen GP, ak a1=-0,5 s q=-4.
Určte tretí, štvrtý a piaty člen GP, ak a1=-0,5 s q=-4. - Aritmetická postupnosť 2
 Určte diferenciu a prvý člen AP, ak a3+a4=48, a7=80.
Určte diferenciu a prvý člen AP, ak a3+a4=48, a7=80. - Kvocient geometrickej
 Určte kvocient GP, ak a1=5 a a1+a2=12.
Určte kvocient GP, ak a1=5 a a1+a2=12. - Siedmak
 Určte siedmy člen GP, ak a1=-3,4, q=5
Určte siedmy člen GP, ak a1=-3,4, q=5 - Tretí člen
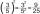 Určte, akú hodnotu bude mať tretí člen postupnosti, ak je postupnosť daná vzťahom: 3^n+93.
Určte, akú hodnotu bude mať tretí člen postupnosti, ak je postupnosť daná vzťahom: 3^n+93. - AP 5
 Určte druhý člen a diferenciu AP, ak a3=5,a a1+a3=16.
Určte druhý člen a diferenciu AP, ak a3=5,a a1+a3=16. - Postupnosti 7873
 Určte prvý člen a diferenciu postupnosti, pre ktorú platí: a1 + a6 = 39; a10 – a4 = 18
Určte prvý člen a diferenciu postupnosti, pre ktorú platí: a1 + a6 = 39; a10 – a4 = 18
