Derivácia spojitej
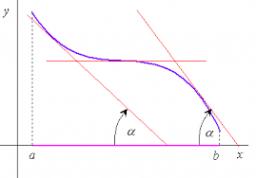
Existuje taká funkcia, ktorá je spojitá a nemá v každom bode deriváciu?
Správna odpoveď:
Zobrazujem 1 komentár:
Www
spojitosť funkcie existenciu derivácie nezaručuje - funkcia môže mať v danom bode zvislú dotyčnicu (čo by zodpovedalo nekonečnej derivácii, čo je nezmysel), prípadne v danom bode nemusí mať dotyčnicu vôbec (v mieste, kde má graf funkcie „špičku“, napr. absolútna hodnota x nemá v bode nula deriváciu).
Existujú dokonca funkcie, ktoré sú spojité v každom bode, ale nemajú v žiadnom bode deriváciu (napr. Weierstrassova funkcia)
Existujú dokonca funkcie, ktoré sú spojité v každom bode, ale nemajú v žiadnom bode deriváciu (napr. Weierstrassova funkcia)
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Distribučná funkcia 2
 Je zadaná spojitá náhodná velicina X: distribučnou funkciou, urcte parametre a; b tak, aby funkcia F (x) bola spojitá a bola distribucnou funkciou náhodnej veliciny X a vyjadrite f (x). P (X < 5) F(x) = 0; x < 3 F(x) = a . x - b; 3 < x < 6 F(x
Je zadaná spojitá náhodná velicina X: distribučnou funkciou, urcte parametre a; b tak, aby funkcia F (x) bola spojitá a bola distribucnou funkciou náhodnej veliciny X a vyjadrite f (x). P (X < 5) F(x) = 0; x < 3 F(x) = a . x - b; 3 < x < 6 F(x - Derivácia
 Existuje funkcia, ktorej derivácia je tá istá funkcia?
Existuje funkcia, ktorej derivácia je tá istá funkcia? - Všeobecná rovnica
 Vo všetkých príkladoch napíšte VŠEOBECNÚ rovnicami priamky, ktorá je nejakým spôsobom zadaná. A) priamka je daná parametricky: x = - 4 + 2p; y = 2 - 3p B) priamka je daná smernicovým tvarom: y = 3x - 1 C) priamka je daná dvomi bodmi: A [3; -3], B [-5; 2]
Vo všetkých príkladoch napíšte VŠEOBECNÚ rovnicami priamky, ktorá je nejakým spôsobom zadaná. A) priamka je daná parametricky: x = - 4 + 2p; y = 2 - 3p B) priamka je daná smernicovým tvarom: y = 3x - 1 C) priamka je daná dvomi bodmi: A [3; -3], B [-5; 2] - Štyria kamaráti
 Na lyžiarske sústredene prišli štyria kamaráti zo 4 svet svetových strán a viedli nasledujúci rozhovor. Karol: "Neprišiel som zo severu ani z juhu. " Mojmír: "Zato ja som prišiel z juhu. " Jozef: "Prišiel som zo severu. " Zdeno: "Ja som z juhu neprišiel.
Na lyžiarske sústredene prišli štyria kamaráti zo 4 svet svetových strán a viedli nasledujúci rozhovor. Karol: "Neprišiel som zo severu ani z juhu. " Mojmír: "Zato ja som prišiel z juhu. " Jozef: "Prišiel som zo severu. " Zdeno: "Ja som z juhu neprišiel.
- Nespojitosť
 Určte bod, v ktorom funkcia sgn x nemá spojitosť.
Určte bod, v ktorom funkcia sgn x nemá spojitosť. - Elektrika - vodič
 Dĺžka vodiča pri teplote 0°C je 119 m a pri každom zvýšení teploty o 1°C sa dĺžka zväčší o 0,15 mm na 1 m dĺžky vodiča. Určte funkciu, ktorá vyjadruje celkovú dĺžku vodiča ako funkciu teploty. Aká je dĺžka tohto vodiča pri teplote -14 °C?
Dĺžka vodiča pri teplote 0°C je 119 m a pri každom zvýšení teploty o 1°C sa dĺžka zväčší o 0,15 mm na 1 m dĺžky vodiča. Určte funkciu, ktorá vyjadruje celkovú dĺžku vodiča ako funkciu teploty. Aká je dĺžka tohto vodiča pri teplote -14 °C? - Rozviňte
 Rozviňte funkciu f(z) do Laurentovho radu v bode z0 pre dané medzikružie f(z)=1/((z-2)*(z-3)) a) z0=2, 03
Rozviňte funkciu f(z) do Laurentovho radu v bode z0 pre dané medzikružie f(z)=1/((z-2)*(z-3)) a) z0=2, 03 - Kvadratická 25111
 Kvadratická funkcia má predpis y=-2x²-3x+8. Vypočítajte funkčnú hodnotu v bode 5, -2 a ½.
Kvadratická funkcia má predpis y=-2x²-3x+8. Vypočítajte funkčnú hodnotu v bode 5, -2 a ½. - Napíšte 8
 Napíšte rovnicu dotyčnice hyperboly 9x²−4y²=36 v bode T =[t1,4].
Napíšte rovnicu dotyčnice hyperboly 9x²−4y²=36 v bode T =[t1,4].
- Dunčo
 Dunčo je uviazaný na reťazi, ktorá je upevnená v rohu dvora. Dvor má tvar štvorca so stranou dlhou 20 metrov. Taká istá dlhá je aj Dunčova reťaz. Sú na dvore miesta kam sa Dunčo nedostane?
Dunčo je uviazaný na reťazi, ktorá je upevnená v rohu dvora. Dvor má tvar štvorca so stranou dlhou 20 metrov. Taká istá dlhá je aj Dunčova reťaz. Sú na dvore miesta kam sa Dunčo nedostane? - Počet koreňov
 Dosaď postupne čísla/0,1,2,3/do rovnice: (X - 1) (x - 3) (x + 1) = 0 Ktorá z nich sú jej riešením? Existuje ešte ďalšie číslo, ktoré je riešením tejto rovnice?
Dosaď postupne čísla/0,1,2,3/do rovnice: (X - 1) (x - 3) (x + 1) = 0 Ktorá z nich sú jej riešením? Existuje ešte ďalšie číslo, ktoré je riešením tejto rovnice? - S=t^3-2t^2-4t-8 6978
 Funkcia posunutia S=t³-2t²-4t-8 udáva polohu telesa v ľubovoľnom čase t. Nájdite jeho zrýchlenie v každom okamihu, keď je rýchlosť nulová.
Funkcia posunutia S=t³-2t²-4t-8 udáva polohu telesa v ľubovoľnom čase t. Nájdite jeho zrýchlenie v každom okamihu, keď je rýchlosť nulová. - Smernica
 Ktorá z funkcii je rastúca? a) y=2-x b) y=20 c) y=(x+2). (-5) d) y=x-2
Ktorá z funkcii je rastúca? a) y=2-x b) y=20 c) y=(x+2). (-5) d) y=x-2 - Kružnica
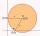 Napište rovnicu kružnice ktorá prechádza bodom [0,6] a dotýka se osy x v bode [5,0]: (x-x_S)²+(y-y_S)²=r²
Napište rovnicu kružnice ktorá prechádza bodom [0,6] a dotýka se osy x v bode [5,0]: (x-x_S)²+(y-y_S)²=r²
- Súmernosť
 Určte obraz bodu A(3,-4,-6) v súmernosti, ktorá je určená rovinou x-y-4z-13=0
Určte obraz bodu A(3,-4,-6) v súmernosti, ktorá je určená rovinou x-y-4z-13=0 - Skutočnosti 19883
 Mierka mapy je 1:100 000. Koľko km je dlhá v skutočnosti cesta, ktorá je na mape dlhá 4,7 cm?
Mierka mapy je 1:100 000. Koľko km je dlhá v skutočnosti cesta, ktorá je na mape dlhá 4,7 cm? - V suteréne
 V suteréne majú miestnosť tvaru kocky s dĺžkou hrany 2,5m, ktorá nemá okná, iba dvere s rozmermi 2*1m. Rozhodli sa, že v nej urobia fínsku saunu. Koľko metrov štvorcových dreveného obkladu budú potrebovať?
V suteréne majú miestnosť tvaru kocky s dĺžkou hrany 2,5m, ktorá nemá okná, iba dvere s rozmermi 2*1m. Rozhodli sa, že v nej urobia fínsku saunu. Koľko metrov štvorcových dreveného obkladu budú potrebovať?
