Z9–I–2
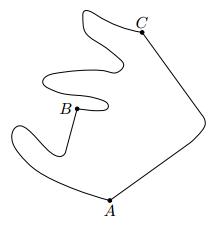
Z bodu A do bodu C vedie náučný chodník prechádzajúci bodom B a inakadiaľ tiež červená turistická značka, pozri obrázok. Okrem toho sa dá použiť aj nezakreslená skratka dlhá 1500 metrov začínajúca v A a ústiaca na náučnom chodníku. Vojtech zistil, že
• výlet z A po červenej do C a po náučnom chodníku späť do A je dlhý 7700 metrov,
• výlet z B po náučnom chodníku do C a potom po červenej do A je dlhý 5800 metrov,
• s využitím skratky je cesta z A do B dlhá 1700 metrov,
• výlet z A po náučnom chodníku do C a späť do A najskôr po náučnom chodníku a potom po skratke je dlhý 8800 metrov.
Určte dĺžku náučného chodníka z A do C. Pokiaľ zadanie pripúšťa viac odpovedí, uveďte všetky
• výlet z A po červenej do C a po náučnom chodníku späť do A je dlhý 7700 metrov,
• výlet z B po náučnom chodníku do C a potom po červenej do A je dlhý 5800 metrov,
• s využitím skratky je cesta z A do B dlhá 1700 metrov,
• výlet z A po náučnom chodníku do C a späť do A najskôr po náučnom chodníku a potom po skratke je dlhý 8800 metrov.
Určte dĺžku náučného chodníka z A do C. Pokiaľ zadanie pripúšťa viac odpovedí, uveďte všetky
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Chcete premeniť jednotku dĺžky?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Turista
 Cesta z miesta A do miesta B meria 11,5 km. Najskôr vedie do kopca, potom po rovine a nakoniec z kopca. Turista ide do kopca rýchlosťou 3 km/h, po rovine 4 km/h, z kopca 5 km/h. Z miesta A do B išiel 2h 54 min, späť 3h 6 min. Aký dlhý je úsek vedúci po ro
Cesta z miesta A do miesta B meria 11,5 km. Najskôr vedie do kopca, potom po rovine a nakoniec z kopca. Turista ide do kopca rýchlosťou 3 km/h, po rovine 4 km/h, z kopca 5 km/h. Z miesta A do B išiel 2h 54 min, späť 3h 6 min. Aký dlhý je úsek vedúci po ro - Turista 13
 Turista prešiel z miesta A do B a späť za 3 hod 41 minút. Cesta z A do B vedie najskôr do kopca, potom po rovine a nakoniec z kopca. Turista išiel do kopca rýchlosťou 4 km/h, po rovine rýchlosťou 5 km/h a z kopca rýchlosťou 6 km/h. Vzdialenosť medzi A a B
Turista prešiel z miesta A do B a späť za 3 hod 41 minút. Cesta z A do B vedie najskôr do kopca, potom po rovine a nakoniec z kopca. Turista išiel do kopca rýchlosťou 4 km/h, po rovine rýchlosťou 5 km/h a z kopca rýchlosťou 6 km/h. Vzdialenosť medzi A a B - Trávnata plocha
 Okolo kruhovej trávnatej plochy je 2 m široký chodník. Vonkajší okraj chodníka tvorí obrubník, ktorého dĺžka je 157 m. Obrubník aj vnútorná strana chodníku spolu tvoria sústredné kružnice. Vypočítajte obsah kruhovej trávnatej plochy a výsledok zaokrúhlite
Okolo kruhovej trávnatej plochy je 2 m široký chodník. Vonkajší okraj chodníka tvorí obrubník, ktorého dĺžka je 157 m. Obrubník aj vnútorná strana chodníku spolu tvoria sústredné kružnice. Vypočítajte obsah kruhovej trávnatej plochy a výsledok zaokrúhlite - Z obce
 Z obce A do obce B vedie peť ciest, z obce B do obce C vedú dve cesty a z obce A do obce C vedie priamo len jedna cesta. Koľkými rôznymi spôsobmi sa dá dostať: A) z obce A do obce C cez obec B? B) akokoľvek z obce A do obce C? C) akokoľvek z obce A do obc
Z obce A do obce B vedie peť ciest, z obce B do obce C vedú dve cesty a z obce A do obce C vedie priamo len jedna cesta. Koľkými rôznymi spôsobmi sa dá dostať: A) z obce A do obce C cez obec B? B) akokoľvek z obce A do obce C? C) akokoľvek z obce A do obc - Skratka
 Cesta z chaty do obchodu vzdialeného 6 km vedie buď po rovnej ceste, po ktorej sa dá ísť rychlosťou 18 km/h a alebo "skratkou". Tá meria len 3,6 km. Lenže cesta z chaty je celá do kopca-rýchlosťou 8 km/h, domov možno ísť z kopca bezpečnú rýchlosťou 24 km/
Cesta z chaty do obchodu vzdialeného 6 km vedie buď po rovnej ceste, po ktorej sa dá ísť rychlosťou 18 km/h a alebo "skratkou". Tá meria len 3,6 km. Lenže cesta z chaty je celá do kopca-rýchlosťou 8 km/h, domov možno ísť z kopca bezpečnú rýchlosťou 24 km/ - Zo Zubrohlavy
 Zo Zubrohlavy do Bobrova vedie jedna asfaltová cesta, dve lesné cesty a jedna cyklocesta. Určite počet spôsobov, ktorými sa dostaneme zo Zubrohlavy do Bobrova a späť. Vypíšte všetky možnosti.
Zo Zubrohlavy do Bobrova vedie jedna asfaltová cesta, dve lesné cesty a jedna cyklocesta. Určite počet spôsobov, ktorými sa dostaneme zo Zubrohlavy do Bobrova a späť. Vypíšte všetky možnosti. - Chodník
 V mestskom parku je kruhový záhon kvetín s priemerom 8m, okolo neho po celej dlžke vedie chodník široký 1m. Aká je rozloha chodníka?
V mestskom parku je kruhový záhon kvetín s priemerom 8m, okolo neho po celej dlžke vedie chodník široký 1m. Aká je rozloha chodníka? - Skratka
 Predstavte si, že idete ku kamarátovi po rovnej ceste. Tá cesta má dĺžku 170 metrov. Potom zahnete doprava a pôjdete ďalších 1000 metrov a ste u kamaráta. Otázka znie, o koľko bude kratšia cesta, keď pôjdete priamou cestou cez pole?
Predstavte si, že idete ku kamarátovi po rovnej ceste. Tá cesta má dĺžku 170 metrov. Potom zahnete doprava a pôjdete ďalších 1000 metrov a ste u kamaráta. Otázka znie, o koľko bude kratšia cesta, keď pôjdete priamou cestou cez pole? - Turistická cesta
 Novo vybudovaná turistická cesta vedie z 25 % cez pole, 3/8 cesty vedie lesom a zvyšných 9 km ide pozdľž rieky. Aká dlhá je cesta?
Novo vybudovaná turistická cesta vedie z 25 % cez pole, 3/8 cesty vedie lesom a zvyšných 9 km ide pozdľž rieky. Aká dlhá je cesta? - Rovnakou 9001
 Starý otec vyšiel na bicykli z domu o 13. hodine. Išiel k rybníku a domu sa vrátil o 15h20min. Tam aj späť išiel rovnakou cestou, ktorá vedie po rovine. Pri rybníku sa zdržal 1hodinu. Koľko minút mu trvala cesta k rybníku?
Starý otec vyšiel na bicykli z domu o 13. hodine. Išiel k rybníku a domu sa vrátil o 15h20min. Tam aj späť išiel rovnakou cestou, ktorá vedie po rovine. Pri rybníku sa zdržal 1hodinu. Koľko minút mu trvala cesta k rybníku? - V parku 4
 V parku je umiestený vo vzdialenosti 3m od chodníku postrekovač. Voda odstrelene do vzdialenosti max 5m. Maximálne akú dĺžku chodníka poleje?
V parku je umiestený vo vzdialenosti 3m od chodníku postrekovač. Voda odstrelene do vzdialenosti max 5m. Maximálne akú dĺžku chodníka poleje? - Chodník ako tetiva
 Vypočítaj dĺžku chodníka, ktorý vedie cez kruhové námestie s priemerom 40 m, ak je chodník od stredu námestia vzdialený 15 m.
Vypočítaj dĺžku chodníka, ktorý vedie cez kruhové námestie s priemerom 40 m, ak je chodník od stredu námestia vzdialený 15 m. - Turistických 70204
 Z parkoviska je možné na vrchol kopca vystúpiť po troch rôznych turistických trasách alebo vyjsť lanovkou a rovnakými štyrmi spôsobmi je možné zostúpiť z kopca späť na parkovisko, ako ilustruje obrázok. Cestou na vrchol kopca a späť je myslený výstup a zo
Z parkoviska je možné na vrchol kopca vystúpiť po troch rôznych turistických trasách alebo vyjsť lanovkou a rovnakými štyrmi spôsobmi je možné zostúpiť z kopca späť na parkovisko, ako ilustruje obrázok. Cestou na vrchol kopca a späť je myslený výstup a zo - Domček Z9–I–5
 Myšky si postavili podzemný domček pozostávajúci z komôrok a tunelkov: • každý tunel vedie z komôrky do komôrky (tzn. žiadny nie je slepý), • z každej komôrky vedú práve tri tunely do troch rôznych komôrok, • z každej komôrky sa dá tunelom dostať do ktore
Myšky si postavili podzemný domček pozostávajúci z komôrok a tunelkov: • každý tunel vedie z komôrky do komôrky (tzn. žiadny nie je slepý), • z každej komôrky vedú práve tri tunely do troch rôznych komôrok, • z každej komôrky sa dá tunelom dostať do ktore - Železnica
 Železničná trať mala na úseku dlhom 5,8 km stúpanie 9 promile. O koľko metrov trať stúpla?
Železničná trať mala na úseku dlhom 5,8 km stúpanie 9 promile. O koľko metrov trať stúpla? - Kytice
 Záhradník viazal kytice po 8 kvetoch a žiadny mu neostal. Potom zistil, že mohol viazať kytice po 6 kvetoch a tiež by mu žiadny neostal. Koľko mal záhradník minimálne a maximálne kvetov, ak ich mal viac ako 50 a menej ako 100?
Záhradník viazal kytice po 8 kvetoch a žiadny mu neostal. Potom zistil, že mohol viazať kytice po 6 kvetoch a tiež by mu žiadny neostal. Koľko mal záhradník minimálne a maximálne kvetov, ak ich mal viac ako 50 a menej ako 100? - Z7-1-6 MO 2018
 Daný je rovnoramenný pravouhlý trojuholník ABS so základňou AB. Na kružnici, ktorá má stred v bode S a prechádza bodmi A a B, leží bod C tak, že trojuholník ABC je rovnoramenný. Určte, koľko bodov C vyhovuje uvedeným podmienkam, a všetky také body zostroj
Daný je rovnoramenný pravouhlý trojuholník ABS so základňou AB. Na kružnici, ktorá má stred v bode S a prechádza bodmi A a B, leží bod C tak, že trojuholník ABC je rovnoramenný. Určte, koľko bodov C vyhovuje uvedeným podmienkam, a všetky také body zostroj
