Z9–I–1
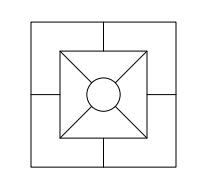
Vo všetkých deviatich poliach obrazca majú byť vyplnené prirodzené čísla tak, aby platilo:
• každé z čísel 2, 4, 6 a 8 je použité aspoň raz,
• štyri z polí vnútorného štvorca obsahujú súčiny čísel zo susediacich polí vonkajšieho štvorca,
• v kruhu je súčet čísel zo susedných polí vnútorného štvorca.
Zistite, ktoré najmenšie a ktoré najväčšie číslo môže byť napísané v kruhu.
• každé z čísel 2, 4, 6 a 8 je použité aspoň raz,
• štyri z polí vnútorného štvorca obsahujú súčiny čísel zo susediacich polí vonkajšieho štvorca,
• v kruhu je súčet čísel zo susedných polí vnútorného štvorca.
Zistite, ktoré najmenšie a ktoré najväčšie číslo môže byť napísané v kruhu.
Správna odpoveď:
Zobrazujem 4 komentáre:
Žiak
Jaká je odpověď nebo postup počítám matematickou olympiádou a nevychází mi to , tady ale také není výsledek ????
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- MO Z6-6-1
 Do prázdnych polí v nasledujúcom obrázku doplňte celé čísla väčšie ako 1 tak, aby v každom tmavšom políčku bol súčin čísel zo susedných svetlejších políčok: Aké je číslo je v strede?
Do prázdnych polí v nasledujúcom obrázku doplňte celé čísla väčšie ako 1 tak, aby v každom tmavšom políčku bol súčin čísel zo susedných svetlejších políčok: Aké je číslo je v strede? - Dve číslice
 Z čísla 547 191 807 vyškrtnite 2 číslice, tak aby ste dostali čo najmenšie číslo deliteľné 5. Napíšte súčet vyškrtnutých čísel
Z čísla 547 191 807 vyškrtnite 2 číslice, tak aby ste dostali čo najmenšie číslo deliteľné 5. Napíšte súčet vyškrtnutých čísel - Osemsten súčet
 Na každej stene pravidelného osemstenu je napísané jedno z čísel 1, 2, 3, 4, 5, 6, 7 a 8, pričom na rôznych stenách sú rôzne čísla. Pri každej steny Janko určil súčet čísla na nej napísaného s číslami troch susedných stien. Takto dostal osem súčtov, ktoré
Na každej stene pravidelného osemstenu je napísané jedno z čísel 1, 2, 3, 4, 5, 6, 7 a 8, pričom na rôznych stenách sú rôzne čísla. Pri každej steny Janko určil súčet čísla na nej napísaného s číslami troch susedných stien. Takto dostal osem súčtov, ktoré - Určte 13
 Určte počet všetkých štvorciferných prirodzených čísel, v dekadickom zápise, v ktorých nie je číslica 0 a zo zvyšných deviatich čísel sa v ňom každá nachádza najviac raz.
Určte počet všetkých štvorciferných prirodzených čísel, v dekadickom zápise, v ktorých nie je číslica 0 a zo zvyšných deviatich čísel sa v ňom každá nachádza najviac raz.
- MO Z8–I–3 - 2017 - Adelka
 Adelka mala na papieri napísané dve čísla. Keď k nim pripísala ešte ich najväčší spoločný deliteľ a najmenší spoločný násobok, dostala štyri rôzne čísla menšie ako 100. S úžasom zistila, že keď vydelí najväčšie z týchto štyroch čísel najmenším, dostane na
Adelka mala na papieri napísané dve čísla. Keď k nim pripísala ešte ich najväčší spoločný deliteľ a najmenší spoločný násobok, dostala štyri rôzne čísla menšie ako 100. S úžasom zistila, že keď vydelí najväčšie z týchto štyroch čísel najmenším, dostane na - Zistite 2
 Zistite súčet všetkých dvojciferných čísel, v ktorých sa číslice líšia o 7.
Zistite súčet všetkých dvojciferných čísel, v ktorých sa číslice líšia o 7. - MO Z6–I–3 2018
 Na obrázku sú naznačené dva rady šesťuholníkových políčok, ktoré doprava pokračujú bez obmedzenia. Do každého políčka doplňte jedno kladné celé číslo tak, aby súčin čísel v ľubovoľných troch navzájom susediacich políčkach bol 2018. Určte číslo, ktoré bude
Na obrázku sú naznačené dva rady šesťuholníkových políčok, ktoré doprava pokračujú bez obmedzenia. Do každého políčka doplňte jedno kladné celé číslo tak, aby súčin čísel v ľubovoľných troch navzájom susediacich políčkach bol 2018. Určte číslo, ktoré bude - Prievan a lístky
 Na piatich lístkoch na stole sú napísané číslice 1,2,3,4,5. Prievan lístky náhodne zamiešal a zložil z nich 5-ciferné číslo. Aká je pravdepodobnosť, že zložil: a, najväčšie možné číslo b, najmenšie možné číslo c, číslo deliteľné piatimi d, párne číslo e,
Na piatich lístkoch na stole sú napísané číslice 1,2,3,4,5. Prievan lístky náhodne zamiešal a zložil z nich 5-ciferné číslo. Aká je pravdepodobnosť, že zložil: a, najväčšie možné číslo b, najmenšie možné číslo c, číslo deliteľné piatimi d, párne číslo e, - MO 2022
 Petra mala napísané prirodzené čísla od 1 do 9. Dve z týchto čísel sčítala, zmazala a výsledný súčet napísala miesto sčítancov. Mala tak napísané osem čísel, ktoré sa jej podarilo rozdeliť do dvoch skupín s rovnakým súčinom. Určite aký najväčší mohol byť
Petra mala napísané prirodzené čísla od 1 do 9. Dve z týchto čísel sčítala, zmazala a výsledný súčet napísala miesto sčítancov. Mala tak napísané osem čísel, ktoré sa jej podarilo rozdeliť do dvoch skupín s rovnakým súčinom. Určite aký najväčší mohol byť
- Dva kódy
 Pán O. si vymyslel dva kódy do trezoru, ktoré po týždni strieda. Oba kódy majú súčin číslic 120. V párny týždeň používa ako kód najmenšie možné číslo s touto vlastnosťou, v nepárny týždeň najväčšie. V žiadnom kóde nie je číslica 1, pretože tlačidlo s tout
Pán O. si vymyslel dva kódy do trezoru, ktoré po týždni strieda. Oba kódy majú súčin číslic 120. V párny týždeň používa ako kód najmenšie možné číslo s touto vlastnosťou, v nepárny týždeň najväčšie. V žiadnom kóde nie je číslica 1, pretože tlačidlo s tout - Medzi dve
 Medzi čísla 6 a 384 vložte niekoľko čísel tak, aby tvorili s danými číslami GP a aby ďalej platilo: a) súčet všetkých čísel je 510 A pre inú GP aby platilo: b) súčet vložených čísel je -132 (Ide o dve rôzne geometrické postupnosti, ale s rovnakými dvoma č
Medzi čísla 6 a 384 vložte niekoľko čísel tak, aby tvorili s danými číslami GP a aby ďalej platilo: a) súčet všetkých čísel je 510 A pre inú GP aby platilo: b) súčet vložených čísel je -132 (Ide o dve rôzne geometrické postupnosti, ale s rovnakými dvoma č - Súčet dvoch prvočísel
 Matematik Christian Goldbach zistil, že každé párne číslo väčšie ako 2 môže byť vyjadrené ako súčet dvoch prvočíselných čísel. Napíšte alebo vyjadrite 2018 ako súčet dvoch prvočísel.
Matematik Christian Goldbach zistil, že každé párne číslo väčšie ako 2 môže byť vyjadrené ako súčet dvoch prvočíselných čísel. Napíšte alebo vyjadrite 2018 ako súčet dvoch prvočísel. - Tri čísla
 Vytvorte z číslic 1 až 9 trojciferné čísla, tak že ich súčet bude najmenší. Aký hodnotu má súčet týchto čísel? (každú číslicu použite len raz)
Vytvorte z číslic 1 až 9 trojciferné čísla, tak že ich súčet bude najmenší. Aký hodnotu má súčet týchto čísel? (každú číslicu použite len raz) - Palko
 Palko má 5 kartičiek s číslicami 0, 1, 6, 7, 9. Kolko nepárnych trojciferných čísel z nich môže utvoriť?
Palko má 5 kartičiek s číslicami 0, 1, 6, 7, 9. Kolko nepárnych trojciferných čísel z nich môže utvoriť?
- Čísla
 a, nájdi najväčšie prirodzené číslo , ktorým sa dajú vydeliť čísla 54 aj 72 ( 120 , 60 aj 42 ) b, nájdi najmenšie prirodzené číslo, ktoré sa dá vydeliť každým z čísel 36 a 48 ( 24,18 a 16 )
a, nájdi najväčšie prirodzené číslo , ktorým sa dajú vydeliť čísla 54 aj 72 ( 120 , 60 aj 42 ) b, nájdi najmenšie prirodzené číslo, ktoré sa dá vydeliť každým z čísel 36 a 48 ( 24,18 a 16 ) - Vyškrtnutých 62744
 Nájdite tri číslice, ktoré je potrebné vyškrtnúť z čísla 214568793, aby vzniklo čo najmenšie číslo. Čomu sa rovná súčet týchto vyškrtnutých číslic?
Nájdite tri číslice, ktoré je potrebné vyškrtnúť z čísla 214568793, aby vzniklo čo najmenšie číslo. Čomu sa rovná súčet týchto vyškrtnutých číslic? - Súčet 13
 Vypočítajte súčet všetkých dvojciferných čísel, ktoré sa dajú vytvoriť z číslic 0, 1 a 3. Číslice sa vo vytvorenom čísle môžu opakovať.
Vypočítajte súčet všetkých dvojciferných čísel, ktoré sa dajú vytvoriť z číslic 0, 1 a 3. Číslice sa vo vytvorenom čísle môžu opakovať.
