Rozklad
Číslo 28 rozložte na dva sčítance tak, aby ich súčin bol maximálny.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Rozložte 7427
 Číslo 135 rozložte na dva sčítance tak aby jeden sčítanec bol o 30 väčší ako dve pätiny druhého sčítanca.
Číslo 135 rozložte na dva sčítance tak aby jeden sčítanec bol o 30 väčší ako dve pätiny druhého sčítanca. - Sčítance
 Číslo 135 rozložte na dva sčítance tak, aby jeden sčítanec bol o 30 väčší ako 2/5 druhého sčítanca.
Číslo 135 rozložte na dva sčítance tak, aby jeden sčítanec bol o 30 väčší ako 2/5 druhého sčítanca. - Sčítance
 Určte dvoch sčítancov čísla 42 tak, aby ich súčin bol čo najmenší.
Určte dvoch sčítancov čísla 42 tak, aby ich súčin bol čo najmenší. - Číslo 111 2
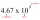 Číslo 111 rozdeľ na 3 sčítance tak aby každý bol o 2 väčší ako predchádzajúce.
Číslo 111 rozdeľ na 3 sčítance tak aby každý bol o 2 väčší ako predchádzajúce. - Sčítanec 7380
 Číslo 4600 rozdeľte na dva sčítance tak, aby jeden sčítanec bol o 700 väčší ako polovica druhého sčítanca.
Číslo 4600 rozdeľte na dva sčítance tak, aby jeden sčítanec bol o 700 väčší ako polovica druhého sčítanca. - Sčítance
 Číslo 109 rozdeľte na dva sčítance tak, aby jeden sčítanec bol o 13 väčší ako 60% druhého. Určite tieto sčítance.
Číslo 109 rozdeľte na dva sčítance tak, aby jeden sčítanec bol o 13 väčší ako 60% druhého. Určite tieto sčítance. - Sčítance
 Číslo 118 rozdelte na dva sčítance tak, aby jeden sčítanec bol o 69 väčší ako 75% druhého sčítanca.
Číslo 118 rozdelte na dva sčítance tak, aby jeden sčítanec bol o 69 väčší ako 75% druhého sčítanca. - Číslo
 Číslo 6600 rozložte na súčin prvočísel.
Číslo 6600 rozložte na súčin prvočísel. - Číslo 40
 Číslo 6 rozdeľte na tri sčítance x, y, z tak, aby x : y = 4 : 3, y : z = 1 : 2.
Číslo 6 rozdeľte na tri sčítance x, y, z tak, aby x : y = 4 : 3, y : z = 1 : 2. - Viete
 Viete číslo 64,9 rozdeliť na tri sčítance tak, aby prvý s druhým boli v pomere 4:5 a tretí s prvým v pomere 7:3?
Viete číslo 64,9 rozdeliť na tri sčítance tak, aby prvý s druhým boli v pomere 4:5 a tretí s prvým v pomere 7:3? - Silu veľkosti
 Silu veľkosti F = 100 N rozložte na dve kolmé zložky s veľkosť'ami F1, F2 tak, aby uhol medzi silami F1 a F bol 43°52'.
Silu veľkosti F = 100 N rozložte na dve kolmé zložky s veľkosť'ami F1, F2 tak, aby uhol medzi silami F1 a F bol 43°52'. - Číslo 110
 Číslo 110 chceme rozdeliť na 3 sčítance tak, aby prvý a druhý boli v pomere 4 : 5 a tretí s prvým v pomere 7 : 3. Vypočítajte najmenší zo sčítancov.
Číslo 110 chceme rozdeliť na 3 sčítance tak, aby prvý a druhý boli v pomere 4 : 5 a tretí s prvým v pomere 7 : 3. Vypočítajte najmenší zo sčítancov. - MO Z6-6-1
 Do prázdnych polí v nasledujúcom obrázku doplňte celé čísla väčšie ako 1 tak, aby v každom tmavšom políčku bol súčin čísel zo susedných svetlejších políčok: Aké je číslo je v strede?
Do prázdnych polí v nasledujúcom obrázku doplňte celé čísla väčšie ako 1 tak, aby v každom tmavšom políčku bol súčin čísel zo susedných svetlejších políčok: Aké je číslo je v strede? - Číslo 39
 Číslo 210 rozdelíme na dva sčítance tak, že jeden sčítanec je o 30 menší ako trojnásobok druhého sčítanca. Určte väčšieho zo sčítancov.
Číslo 210 rozdelíme na dva sčítance tak, že jeden sčítanec je o 30 menší ako trojnásobok druhého sčítanca. Určte väčšieho zo sčítancov. - (2riešenie): 7315
 Ján opisoval príklad, ale zabudol na početné znamienka. Doplň ich tak, aby bol výsledok správny. (2riešenie): 3 3 3 3=8
Ján opisoval príklad, ale zabudol na početné znamienka. Doplň ich tak, aby bol výsledok správny. (2riešenie): 3 3 3 3=8 - Rozložte
 Rozložte na súčin prvočísel čísla a určte jeho ciferný súčet: 180, 232, 460, 240, 365,
Rozložte na súčin prvočísel čísla a určte jeho ciferný súčet: 180, 232, 460, 240, 365, - Kôpky
 Anička má celkom 702 eurocentov. Peniaze musia rozdeliť na rôzny počet kôpok tak, aby na každej kupca bol rovnaký počet eurocentov. Koľko má možností?
Anička má celkom 702 eurocentov. Peniaze musia rozdeliť na rôzny počet kôpok tak, aby na každej kupca bol rovnaký počet eurocentov. Koľko má možností?
