Rovnoramenný - Z7–I–5
Je daný trojuholník ABC so stranami /AB/ = 3 cm, /BC/ = 10 cm a uhlom ABC = 120°. Narysujte všetky body X tak, aby platilo, že trojuholník BCX je rovnoramenný a súčasne trojuholník ABX je rovnoramenný so základňou AB.
Správna odpoveď:
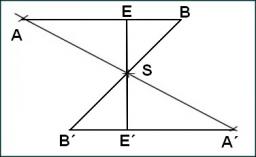
Zobrazujem 2 komentáre:
Mo - Radce
; podle dohody je úhel u prostředního vrcholu, pokud je jeho název dán pomocí vrcholu trojúhelníku, tudíž úhel ABC má vrchol v bobu B, nikoliv v bodu A. V tom případě není správně délka strany BC.
Samozřejmě je pravda, že průsečíkem os stran BC a AB získám bod X, pro který platí uvedené podmínky. Tentýž bod by ale existoval i v opačné polorovině. Tahle situace platí za předpokladu, že BC je základna rovnoramenného trojúhelníku.
Pokud by BC nebyla základna, ale rameno rovnoramenného trojúhelníku, tak si myslím, že kdybych narýsoval kružnici o poloměru 10 cm se středem v bodu C, dostanu dva průsečíky s osou strany AB. Oba body X, které by vznikly, by měly vyhovovat a tytéž body by měly být i v opačné polorovině.
Když udělám tutéž kružnici se středem v bodu B, tak zase vzniknou dva průsečíky s osou strany AB, které ale budou sobě navzájem obrazem v osové souměrnosti. Takže přemýšlím o tom, že těch bodů bude celkem 8. Ještě jsem to ale nerýsoval, protože mi odešlo kružítko...
Samozřejmě je pravda, že průsečíkem os stran BC a AB získám bod X, pro který platí uvedené podmínky. Tentýž bod by ale existoval i v opačné polorovině. Tahle situace platí za předpokladu, že BC je základna rovnoramenného trojúhelníku.
Pokud by BC nebyla základna, ale rameno rovnoramenného trojúhelníku, tak si myslím, že kdybych narýsoval kružnici o poloměru 10 cm se středem v bodu C, dostanu dva průsečíky s osou strany AB. Oba body X, které by vznikly, by měly vyhovovat a tytéž body by měly být i v opačné polorovině.
Když udělám tutéž kružnici se středem v bodu B, tak zase vzniknou dva průsečíky s osou strany AB, které ale budou sobě navzájem obrazem v osové souměrnosti. Takže přemýšlím o tom, že těch bodů bude celkem 8. Ještě jsem to ale nerýsoval, protože mi odešlo kružítko...
7 rokov 1 Like
Tipy na súvisiace online kalkulačky
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Narysujte
 Narysujte rovnoramenný trojuholník ABC, ak AB=7cm, veľkosť uhla ABC je 47°, ramená |AC| = |BC|. Odmerajte veľkosť strany BC v mm.
Narysujte rovnoramenný trojuholník ABC, ak AB=7cm, veľkosť uhla ABC je 47°, ramená |AC| = |BC|. Odmerajte veľkosť strany BC v mm. - Trojuholník ABC
 V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC.
V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC. - Hlavný vrchol
 ABC je rovnoramenný trojuholník so základňou BC a hlavným vrcholom A. Uhol pri vrchole A má veľkosť 18°. Akú veľkosť bude mať uhol pri vrchole B?
ABC je rovnoramenný trojuholník so základňou BC a hlavným vrcholom A. Uhol pri vrchole A má veľkosť 18°. Akú veľkosť bude mať uhol pri vrchole B? - Zastroj
 Zastroj rovnoramenný trojuholník ABY zo základňou AB dĺžky 5 cm a uhlom pri hlavnom vrchole veľkosti 50°. Zapíše postup konštrukcie.
Zastroj rovnoramenný trojuholník ABY zo základňou AB dĺžky 5 cm a uhlom pri hlavnom vrchole veľkosti 50°. Zapíše postup konštrukcie.
- Z7-1-6 MO 2018
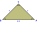 Daný je rovnoramenný pravouhlý trojuholník ABS so základňou AB. Na kružnici, ktorá má stred v bode S a prechádza bodmi A a B, leží bod C tak, že trojuholník ABC je rovnoramenný. Určte, koľko bodov C vyhovuje uvedeným podmienkam, a všetky také body zostroj
Daný je rovnoramenný pravouhlý trojuholník ABS so základňou AB. Na kružnici, ktorá má stred v bode S a prechádza bodmi A a B, leží bod C tak, že trojuholník ABC je rovnoramenný. Určte, koľko bodov C vyhovuje uvedeným podmienkam, a všetky také body zostroj - V trojuholníku
 V trojuholníku ABC je [AB]=20cm, [BC]=10cm, A=30°. Zostroj trojuholník A'B'C' podobný s trojuholníkom ABC, ak koeficient podobnosti je 0,5
V trojuholníku ABC je [AB]=20cm, [BC]=10cm, A=30°. Zostroj trojuholník A'B'C' podobný s trojuholníkom ABC, ak koeficient podobnosti je 0,5 - Rovnoramenný trojuholník
 Vypočítajte obsah a obvod rovnoramenného trojuholníka ABC so základňou AB, a = 6 cm, c = 7 cm.
Vypočítajte obsah a obvod rovnoramenného trojuholníka ABC so základňou AB, a = 6 cm, c = 7 cm. - Kosodĺžnik 8
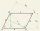 Zostroj rovnobežník (kosodĺžnik) ABCD, |AB|= 4 cm alfa=30° |BD|= 5 cm.
Zostroj rovnobežník (kosodĺžnik) ABCD, |AB|= 4 cm alfa=30° |BD|= 5 cm. - Rovnoramennom 83157
 Použitím kosínovej vety dokážte, že v rovnoramennom trojuholníku ABC so základňou AB platí, že c=2a cos α.
Použitím kosínovej vety dokážte, že v rovnoramennom trojuholníku ABC so základňou AB platí, že c=2a cos α.
- RR trojuholník
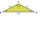 Vypočítajte výšku na základňu rovnoramenného trojuholníka ABC so základňou AB, AB = c = 10 cm a ramenami a = b = 13 cm
Vypočítajte výšku na základňu rovnoramenného trojuholníka ABC so základňou AB, AB = c = 10 cm a ramenami a = b = 13 cm - Rovnoramenný lichobežník 9
 Narysuj rovnoramenný lichobežník ABDC, ak a=6cm, v=5cm, beta=60 stupňov. /náčrt, postup, konštrukcia/
Narysuj rovnoramenný lichobežník ABDC, ak a=6cm, v=5cm, beta=60 stupňov. /náčrt, postup, konštrukcia/ - Vypočítajte 195
 Vypočítajte všetky vnútorné uhly v rovnoramennom trojuholníku ABC ak vieme, že BC je základňa a navyše vieme: |∢BAC|=α; |∢BCA|=4α
Vypočítajte všetky vnútorné uhly v rovnoramennom trojuholníku ABC ak vieme, že BC je základňa a navyše vieme: |∢BAC|=α; |∢BCA|=4α - Päťuholník
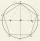 Vo vnútri pravidelného päťuholníka ABCDE je bod P taký, že trojuholník ABP je rovnostranný. Aký veľký je uhol BCP? Urob si náčrtok.
Vo vnútri pravidelného päťuholníka ABCDE je bod P taký, že trojuholník ABP je rovnostranný. Aký veľký je uhol BCP? Urob si náčrtok. - Trojuholník 25851
 A. Zostrojte ∆ABC taký, že c = 55 mm, α = 45°, β = 60°. B. Narysujte ľubovoľný ostrouhlý trojuholník a zostrojte jeho výšky.
A. Zostrojte ∆ABC taký, že c = 55 mm, α = 45°, β = 60°. B. Narysujte ľubovoľný ostrouhlý trojuholník a zostrojte jeho výšky.
- V pravouhlom 11
 V pravouhlom trojuholníku ABC vypočítajte veľkosť vnútorných uhlov, ak/AB/ = 13 cm; /BC/ = 12 cm a/AC/ = 5 cm.
V pravouhlom trojuholníku ABC vypočítajte veľkosť vnútorných uhlov, ak/AB/ = 13 cm; /BC/ = 12 cm a/AC/ = 5 cm. - Rovnoramenný lichobežník 2
 Daný je rovnoramenný lichobežník ABCD, v ktorom platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho strane BC je bod K taký, že |BK| = 2|KC|, na jeho strane CD je bod L taký, že |CL|= 2|LD|, a na jeho strane DA je bod M taký, že|DM|= 2|MA|. Určte veľkosti vnútorných
Daný je rovnoramenný lichobežník ABCD, v ktorom platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho strane BC je bod K taký, že |BK| = 2|KC|, na jeho strane CD je bod L taký, že |CL|= 2|LD|, a na jeho strane DA je bod M taký, že|DM|= 2|MA|. Určte veľkosti vnútorných - V rovine
 V rovine je daný trojuholník ABC. A(-3,5), B(2,3), C(-1,-2) zapíšte súradnice vektorov u, v, w ak u=AB, v=AC, w=BC. Zapíšte súradnice stredov úsečiek SAB(. .), SAC(. .. ), SBC(. .. )
V rovine je daný trojuholník ABC. A(-3,5), B(2,3), C(-1,-2) zapíšte súradnice vektorov u, v, w ak u=AB, v=AC, w=BC. Zapíšte súradnice stredov úsečiek SAB(. .), SAC(. .. ), SBC(. .. )
