MO-I-Z6
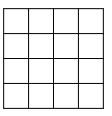
Štvorec so stranou 4 cm je rozdelený na štvorčeky so stranou 1 cm ako na obrázku. Rozdeľte štvorec pozdĺž vyznačených čiar na dva útvary s obvodom 16 cm. Nájdite aspoň tri rôzne riešenia (tzn. také tri riešenia, aby žiadny útvar jedného riešenia nebol zhodný so žiadnym útvarom iného riešenia).
Správna odpoveď:
Zobrazujem 2 komentáre:
Www
jedno riesenie su dva utvary:
####
#
##
a druhy s obvodom je doplnok do stvorca, tiez ma obvod 16.
Staci sa s tym pohrat - utvary musia mat priblizne rovnaky obsah aby mali rovnaky obvod.
####
#
##
a druhy s obvodom je doplnok do stvorca, tiez ma obvod 16.
Staci sa s tym pohrat - utvary musia mat priblizne rovnaky obsah aby mali rovnaky obvod.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Štvorcová sieť
 Štvorcová sieť sa skladá zo štvorca so stranou dĺžky 1cm. Narysujte do nej aspoň tri rôzne obrazce také, aby každý mal obsah 6 cm² a obvod 12cm a aby ich strany splývali s priamkami siete.
Štvorcová sieť sa skladá zo štvorca so stranou dĺžky 1cm. Narysujte do nej aspoň tri rôzne obrazce také, aby každý mal obsah 6 cm² a obvod 12cm a aby ich strany splývali s priamkami siete. - Zoraďte
 Zoraďte dané útvary podľa ich plošného obsahu, zostupne: štvorec s obvodom = 16 cm; Obdĺžnik so stranou a = 3 cm a obvodom o = 16 cm; Pravouhlý trojuholník s odvesnou dlhou 4,125 cm a preponou 8,125 cm.
Zoraďte dané útvary podľa ich plošného obsahu, zostupne: štvorec s obvodom = 16 cm; Obdĺžnik so stranou a = 3 cm a obvodom o = 16 cm; Pravouhlý trojuholník s odvesnou dlhou 4,125 cm a preponou 8,125 cm. - Rozdeľte 2
 Rozdeľte štvorec so stranou dĺžky 12 cm na tri obdĺžniky s rovnakými obvodmi tak, aby tieto obvody boli čo najmenšie.
Rozdeľte štvorec so stranou dĺžky 12 cm na tri obdĺžniky s rovnakými obvodmi tak, aby tieto obvody boli čo najmenšie. - Rozhodni 2
 Rozhodni, ktoré útvary majú väčší obsah: a) štvorec so stranou 8cm alebo b) dva obdížniky so stranami 5cm a 15cm? Zapíš výsledok ako 1 alebo 2 (obdĺžniky)
Rozhodni, ktoré útvary majú väčší obsah: a) štvorec so stranou 8cm alebo b) dva obdížniky so stranami 5cm a 15cm? Zapíš výsledok ako 1 alebo 2 (obdĺžniky) - Útvar kríž
 Útvar na obrázku je zložený z rovnakých štvorcov a má obsah 45cm². Aký je jeho obvod?
Útvar na obrázku je zložený z rovnakých štvorcov a má obsah 45cm². Aký je jeho obvod? - Rozdeľte 4
 Rozdeľte obdĺžnik so stranami dlhými 60 mm a 84 mm na tri obdĺžniky s rovnakým obvodom.
Rozdeľte obdĺžnik so stranami dlhými 60 mm a 84 mm na tri obdĺžniky s rovnakým obvodom. - MO-Z5-3-66
 Na obrázku je štvorcová dlaždica so stranou dĺžky 10 dm, ktorá je zložená zo štyroch zhodných obdĺžnikov a malého štvorca. Obvod malého štvorca je päťkrát menší ako obvod celej dlaždice. Určte rozmery obdĺžnikov.
Na obrázku je štvorcová dlaždica so stranou dĺžky 10 dm, ktorá je zložená zo štyroch zhodných obdĺžnikov a malého štvorca. Obvod malého štvorca je päťkrát menší ako obvod celej dlaždice. Určte rozmery obdĺžnikov. - Myška Hryzka
 Myška Hryzka našla 27 rovnakých kociek syra. Najskôr si z nich poskladala veľkú kocku a chvíľu počkala, než sa syrové kocôčky k sebe prilepili. Potom z každej steny veľkej kocky vyhryzie strednú kocôčku. Potom zjedla aj kocôčky, ktorá bola v stredu veľkej
Myška Hryzka našla 27 rovnakých kociek syra. Najskôr si z nich poskladala veľkú kocku a chvíľu počkala, než sa syrové kocôčky k sebe prilepili. Potom z každej steny veľkej kocky vyhryzie strednú kocôčku. Potom zjedla aj kocôčky, ktorá bola v stredu veľkej - Štvoruholník ASBE
 Na obrázku je štvorec ABCD so stredom S a stranou dlhou 8 cm. Bod E je l'ubovoľný bod strany CD rozny od C a D. Vypočítajte obsah štvoruholníka ASBE v cm².
Na obrázku je štvorec ABCD so stredom S a stranou dlhou 8 cm. Bod E je l'ubovoľný bod strany CD rozny od C a D. Vypočítajte obsah štvoruholníka ASBE v cm². - Rozdeľte 3
 Rozdeľte štvorcovú záhradu s obvodom 124 m na dve obdĺžnikové záhrady tak, aby plot jednej záhrady bol o 10 m dlhší ako plot druhej záhrady. Aké rozmery budú mať tieto obdĺžnikové záhrady?
Rozdeľte štvorcovú záhradu s obvodom 124 m na dve obdĺžnikové záhrady tak, aby plot jednej záhrady bol o 10 m dlhší ako plot druhej záhrady. Aké rozmery budú mať tieto obdĺžnikové záhrady? - Štvorec ABCD
 Zostrojte štvorec ABCD so stredom S [3,2] a stranou a = 4cm. Vrchol A leží na osi x. Zostrojte jeho obraz v posunutí danom orientovanou úsečkou SS'; S` [-1, - 4].
Zostrojte štvorec ABCD so stredom S [3,2] a stranou a = 4cm. Vrchol A leží na osi x. Zostrojte jeho obraz v posunutí danom orientovanou úsečkou SS'; S` [-1, - 4]. - Obdĺžnik - kto má pravdu
 Obdĺžnik je rozdelený na 7 políčok. Na každé políčko sa má napísať práve jedno z čísel 1, 2 a 3. Mirek tvrdia, že to možno vykonať tak, aby súčet dvoch vedľa seba napísaných čísel bol zakaždým iný. Zuzka naopak tvrdia, že to možné nie je. Rozhodnite, kto
Obdĺžnik je rozdelený na 7 políčok. Na každé políčko sa má napísať práve jedno z čísel 1, 2 a 3. Mirek tvrdia, že to možno vykonať tak, aby súčet dvoch vedľa seba napísaných čísel bol zakaždým iný. Zuzka naopak tvrdia, že to možné nie je. Rozhodnite, kto - Záhradu
 Záhradu tvaru štvorca so stranou 16,2 m máme zasiať trávou. Koľko kg trávového semena potrebujeme ak na 1 meter štvorcový treba 25 gramov.
Záhradu tvaru štvorca so stranou 16,2 m máme zasiať trávou. Koľko kg trávového semena potrebujeme ak na 1 meter štvorcový treba 25 gramov. - Z5 – I – 2 MO 2018
 Tereza dostala štyri zhodné pravouhlé trojuholníky so stranami dĺžok 3 cm, 4 cm a 5 cm. Z týchto trojuholníkov (nie nutne zo všetkých štyroch) skúšala skladať nové útvary. Postupne sa jej podarilo zložiť štvoruholníky s obvodom 14 cm, 18 cm, 22 cm a 26 cm
Tereza dostala štyri zhodné pravouhlé trojuholníky so stranami dĺžok 3 cm, 4 cm a 5 cm. Z týchto trojuholníkov (nie nutne zo všetkých štyroch) skúšala skladať nové útvary. Postupne sa jej podarilo zložiť štvoruholníky s obvodom 14 cm, 18 cm, 22 cm a 26 cm - Oplotenie 3
 Pozemok je v tvare štvorca so stranou 65,4 metra. A 1 meter pletiva stojí 2,30 eur. Koľko eur zaplatíme za oplotenie pozemku?
Pozemok je v tvare štvorca so stranou 65,4 metra. A 1 meter pletiva stojí 2,30 eur. Koľko eur zaplatíme za oplotenie pozemku? - Z8 – I – 3 MO 2018
 Peter narysoval pravidelný šesťuholník, ktorého vrcholy ležali na kružnici dĺžky 16 cm. Potom pre každý vrchol tohto šesťuholníka narysoval kružnicu so stredom v tomto vrchole, ktorá prechádzala jeho dvoma susednými vrcholmi. Vznikol tak útvar ako na obrá
Peter narysoval pravidelný šesťuholník, ktorého vrcholy ležali na kružnici dĺžky 16 cm. Potom pre každý vrchol tohto šesťuholníka narysoval kružnicu so stredom v tomto vrchole, ktorá prechádzala jeho dvoma susednými vrcholmi. Vznikol tak útvar ako na obrá - Na mape 7
 Na mape s mierkou 1:30 000 je pozemok znázornený štvorcom so stranou 6cm. Akú výmeru má pozemok v skutočnosti? Koľkokrát je skutočný pozemok väčší ako jeho obraz v mape?
Na mape s mierkou 1:30 000 je pozemok znázornený štvorcom so stranou 6cm. Akú výmeru má pozemok v skutočnosti? Koľkokrát je skutočný pozemok väčší ako jeho obraz v mape?
