Dôkaz - MO - C – I – 3
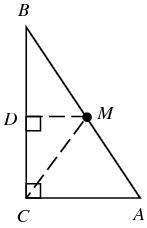
Päta výšky z vrcholu C v trojuholníku ABC delí stranu AB v pomere 1:2. Dokážte, že pri zvyčajnom označení dĺžok strán trojuholníka ABC platí nerovnosť 3∣a−b∣<c.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Štvorce
 Na dvoma stranami trojuholníka ABC sú zostrojené štvorce. Obsah štvorca nad stranou BC je 25 cm². Veľkosť výšky vc na stranu AB je 3 cm. Pata P výšky vc delí stranu AB v pomere 2:1. Strana AC je dlhšia ako strana BC. Vypočítajte v cm dĺžku strany AB. Vypo
Na dvoma stranami trojuholníka ABC sú zostrojené štvorce. Obsah štvorca nad stranou BC je 25 cm². Veľkosť výšky vc na stranu AB je 3 cm. Pata P výšky vc delí stranu AB v pomere 2:1. Strana AC je dlhšia ako strana BC. Vypočítajte v cm dĺžku strany AB. Vypo - Kosodĺžnik 5
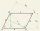 Určte obvod a obsah kosodĺžnika ABCD, ktorého kratšia strana AD má dĺžku 5 cm a päta výšky vedené vrcholom D k strane AB delí stranu AB na dva úseky dĺžok 3 cm a 4 cm.
Určte obvod a obsah kosodĺžnika ABCD, ktorého kratšia strana AD má dĺžku 5 cm a päta výšky vedené vrcholom D k strane AB delí stranu AB na dva úseky dĺžok 3 cm a 4 cm. - Trojuholník ABC
 V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC.
V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC. - Rovnoramennom 83157
 Použitím kosínovej vety dokážte, že v rovnoramennom trojuholníku ABC so základňou AB platí, že c=2a cos α.
Použitím kosínovej vety dokážte, že v rovnoramennom trojuholníku ABC so základňou AB platí, že c=2a cos α. - V pravouhlom 12
 V pravouhlom trojuholníku má prepona dĺžku 24cm. Päta výšky na preponu ju delí na dve časti v pomere 2:4. Akú veľkosť v cm má výška na preponu? Vypočítajte v centimetroch obvod tohto pravouhlého trojuholníka.
V pravouhlom trojuholníku má prepona dĺžku 24cm. Päta výšky na preponu ju delí na dve časti v pomere 2:4. Akú veľkosť v cm má výška na preponu? Vypočítajte v centimetroch obvod tohto pravouhlého trojuholníka. - Trojuholníka 81019
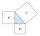 V pravouhlom trojuholníku ABC (AB je prepona) platí a : b = 24 : 7 a výška na stranu c = 12,6 cm. Vypočítajte dĺžky strán trojuholníka ABC.
V pravouhlom trojuholníku ABC (AB je prepona) platí a : b = 24 : 7 a výška na stranu c = 12,6 cm. Vypočítajte dĺžky strán trojuholníka ABC. - C – I – 3 MO 2018
 Nech a, b, c sú kladné reálne čísla, ktorých súčet je 3, a každé z nich je nanajvýš 2. Dokážte, že platí nerovnosť: a2 + b2 + c2 + 3abc < 9
Nech a, b, c sú kladné reálne čísla, ktorých súčet je 3, a každé z nich je nanajvýš 2. Dokážte, že platí nerovnosť: a2 + b2 + c2 + 3abc < 9 - Trojuholníka 81613
 V rovine je umiestnený trojuholník ABC s pravým uhlom pri vrchole C, pre ktorý platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určite hodnotu x b) určite súradnice bodu M, ktorý je stredom úsečky AB c) dokážte že vektory AB a CM sú kolmé d) určite v
V rovine je umiestnený trojuholník ABC s pravým uhlom pri vrchole C, pre ktorý platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určite hodnotu x b) určite súradnice bodu M, ktorý je stredom úsečky AB c) dokážte že vektory AB a CM sú kolmé d) určite v - Ťažisko
 V rovnoramennom trojuholníku ABC je pomer dĺžok základne AB a výšky na základňu 10:12. Rameno má dĺžku 26 cm. Ak je T ťažiskom trojuholníka ABC, vypočítajte obsah trojuholníka ABT.
V rovnoramennom trojuholníku ABC je pomer dĺžok základne AB a výšky na základňu 10:12. Rameno má dĺžku 26 cm. Ak je T ťažiskom trojuholníka ABC, vypočítajte obsah trojuholníka ABT. - Trojuholník PRT
 V rovnoramennom pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C platí o súradniciach bodov: A (-1, 2); C (-5, -2) Vypočítajte dĺžku strany AB.
V rovnoramennom pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C platí o súradniciach bodov: A (-1, 2); C (-5, -2) Vypočítajte dĺžku strany AB. - Stred prepony
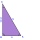 Pre vnútorné uhly trojuholnika ABC platí, že alfa beta a gama sú v pomere 1:2:3. Najdlhšia strana trojuholníka AB má dĺžku 30cm. Vypočítaj obvod trojuholnika CBS, ak S je stred strany AB
Pre vnútorné uhly trojuholnika ABC platí, že alfa beta a gama sú v pomere 1:2:3. Najdlhšia strana trojuholníka AB má dĺžku 30cm. Vypočítaj obvod trojuholnika CBS, ak S je stred strany AB - V trojuholníku 5
 V trojuholníku ABC platí, že výška na stranu a je 6cm. Výška na stranu b sa rovná 9 cm. Strana "a" je o 4cm dlhšia ako strana "b". Vypočítajte dĺžky strán a, b.
V trojuholníku ABC platí, že výška na stranu a je 6cm. Výška na stranu b sa rovná 9 cm. Strana "a" je o 4cm dlhšia ako strana "b". Vypočítajte dĺžky strán a, b. - Trojuholník 73764
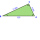 Trojuholník ABC má uhol C rozpolený a pretína stranu AB v bode D. Uhol A (alfa) meria 20 stupňov a uhol B meria 40 stupňov. Otázkou je určiť rozdiel dĺžok strán |AB|-|AC|, ak dĺžka |AD|=1.
Trojuholník ABC má uhol C rozpolený a pretína stranu AB v bode D. Uhol A (alfa) meria 20 stupňov a uhol B meria 40 stupňov. Otázkou je určiť rozdiel dĺžok strán |AB|-|AC|, ak dĺžka |AD|=1. - Trojuholníku 83150
 V trojuholníku ABC poznáte pomer dĺžok strán a:b:c=3:4:6. Vypočítajte veľkosti uhlov trojuholníka ABC.
V trojuholníku ABC poznáte pomer dĺžok strán a:b:c=3:4:6. Vypočítajte veľkosti uhlov trojuholníka ABC. - MO - trojuholníky
 Na stranách AB a AC trojuholníka ABC leží postupne body E a F, na úsečke EF leží bod D. Přmky EF a BC sú rovnobežné a súčasne platí FD:DE = AE:EB = 2:1. Trojuholník ABC má obsah 27 hektárov a úsečkami EF, AD a DB je rozdelený na štyri časti. Určite obsahy
Na stranách AB a AC trojuholníka ABC leží postupne body E a F, na úsečke EF leží bod D. Přmky EF a BC sú rovnobežné a súčasne platí FD:DE = AE:EB = 2:1. Trojuholník ABC má obsah 27 hektárov a úsečkami EF, AD a DB je rozdelený na štyri časti. Určite obsahy - Vrcholy T3D
 Vrcholy trojuholníka ABC sú: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Vypočítajte dĺžky strán AB, AC a uhol pri vrchole A.
Vrcholy trojuholníka ABC sú: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Vypočítajte dĺžky strán AB, AC a uhol pri vrchole A. - Ťažnice
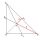 Ťažnica t na stranu b (tb) v trojuholníku ABC má dĺžku 12 cm. a, aká je vzdialenosť ťažiska T od vrcholu B? b, urči vzdialenosť ťažiska T od strany b.
Ťažnica t na stranu b (tb) v trojuholníku ABC má dĺžku 12 cm. a, aká je vzdialenosť ťažiska T od vrcholu B? b, urči vzdialenosť ťažiska T od strany b.
