Tehly 3
Na stavbu vozili tehly v troch nákladných autách. Jedno odviezlo naraz n tehál, druhé o m tehál menej ako prvé a na tretie sa zmestilo o 300 tehál viac ako na prvé auto. Prvé auto išlo 4-krát denne, najväčšie auto išlo 3-krát denne a najmenšie 5-krát denne.
Koľko tehál priviezli:
a/ všetky autá za jeden deň,
b/ všetky autá za jeden týždeň /v nedeľu nepracovali/?
Koľko tehál priviezli:
a/ všetky autá za jeden deň,
b/ všetky autá za jeden týždeň /v nedeľu nepracovali/?
Správna odpoveď:

Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Repná kampaň
 Na poli prebieha zber repy. Repa sa odváža do 3 závodov, 3 nákladnými autami. Prvé auto sa vráti na pole 3x do hodiny, druhé auto po 30tich minútach a tretie auto 5x za hodinu. Všetky autá vyšla v 8 ráno. Koľko áut napočítame na poli medzi 9,30 a 11,20?
Na poli prebieha zber repy. Repa sa odváža do 3 závodov, 3 nákladnými autami. Prvé auto sa vráti na pole 3x do hodiny, druhé auto po 30tich minútach a tretie auto 5x za hodinu. Všetky autá vyšla v 8 ráno. Koľko áut napočítame na poli medzi 9,30 a 11,20? - Spracovateľských 31971
 Na poli prebieha zber repy. Repa sa odváža do 3 rôznych spracovateľských závodov 3 nákladnými autami. Jedno auto sa stihne na pole vrátiť 3x do hodiny, druhé po 30tich minútach a tretie má najkratšiu cestu, preto sa obráti 5x za hodinu. Všetky autá vyšla
Na poli prebieha zber repy. Repa sa odváža do 3 rôznych spracovateľských závodov 3 nákladnými autami. Jedno auto sa stihne na pole vrátiť 3x do hodiny, druhé po 30tich minútach a tretie má najkratšiu cestu, preto sa obráti 5x za hodinu. Všetky autá vyšla - Splachovaním 5968
 Federálne zákony vyžadujú, aby všetky toalety predávané v Spojených štátoch amerických nepoužívali viac ako 1 3/5 galónu vody na jedno spláchnutie. Pred touto legislatívou konvenčné toalety používali 3 2/5 galónu vody na jedno spláchnutie. Zistite množstv
Federálne zákony vyžadujú, aby všetky toalety predávané v Spojených štátoch amerických nepoužívali viac ako 1 3/5 galónu vody na jedno spláchnutie. Pred touto legislatívou konvenčné toalety používali 3 2/5 galónu vody na jedno spláchnutie. Zistite množstv - Materiál 23301
 Materiál, ktorého hmotnosť bola 18,2 t, odvážala tri autá. Druhé viezlo o 20% viac ako prvé a tretie 20% viac ako druhé. Koľko ton viezol každé?
Materiál, ktorého hmotnosť bola 18,2 t, odvážala tri autá. Druhé viezlo o 20% viac ako prvé a tretie 20% viac ako druhé. Koľko ton viezol každé? - Nastrieľali 3524
 štyri hokejové mužstvá nastrieľali v turnaji 337 gólov. druhé družstvo dalo o 16 gólov menej ako prvé, tretie o 17 menej ako druhé a štvrté o 30 gólov menej ako druhé. Koľko gólov dalo každé mužstvo?
štyri hokejové mužstvá nastrieľali v turnaji 337 gólov. druhé družstvo dalo o 16 gólov menej ako prvé, tretie o 17 menej ako druhé a štvrté o 30 gólov menej ako druhé. Koľko gólov dalo každé mužstvo? - Súčin 16
 Súčin troch čísel je 224. Prvé z nich je 10, druhé je 50-krát menšie ako prvé. Vypočítajte tretie číslo.
Súčin troch čísel je 224. Prvé z nich je 10, druhé je 50-krát menšie ako prvé. Vypočítajte tretie číslo. - Šofér - vodič
 Šofér nákladného auta vozí tehly na stavbu. Keby išiel trikrát denne, navozil by tehly potrebné na stavbu za 12 dní. Koľkokrát denne musí ísť, aby prácu skončil o tri dni skôr?
Šofér nákladného auta vozí tehly na stavbu. Keby išiel trikrát denne, navozil by tehly potrebné na stavbu za 12 dní. Koľkokrát denne musí ísť, aby prácu skončil o tri dni skôr? - Na ceste 3
 Na ceste sa míňali dve oproti sebe idúce autá a ďalej v ceste pokračovali. Jedno auto prešlo za 1 sekundu 17,5 m a druhé 15,25m. Ako ďaleko budú od seba vzdialené tieto autá za pol hodiny?
Na ceste sa míňali dve oproti sebe idúce autá a ďalej v ceste pokračovali. Jedno auto prešlo za 1 sekundu 17,5 m a druhé 15,25m. Ako ďaleko budú od seba vzdialené tieto autá za pol hodiny? - Sučin 7
 Sučin troch čísel je 224. Prvé z nich je 10, druhé je 50 - krát menšie ako prvé. Vypočítajte tretie číslo.
Sučin troch čísel je 224. Prvé z nich je 10, druhé je 50 - krát menšie ako prvé. Vypočítajte tretie číslo. - Urči súčet
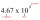 Urči súčet troch čísel, ak prvé číslo je 328, druhé je o 28 menšie a tretie predstavuje ¼ prvého čísla.
Urči súčet troch čísel, ak prvé číslo je 328, druhé je o 28 menšie a tretie predstavuje ¼ prvého čísla. - Predchádzali 5310
 V meste mali troje vežné hodiny. Jedny išli správne, druhé sa denne o 10 minút predchádzali a tretie sa denne o 12 minút oneskorovali. Jedného dňa odbíjali všetky hodiny dvanástu hodinu naraz. Za ako dlho to tak opäť bude?
V meste mali troje vežné hodiny. Jedny išli správne, druhé sa denne o 10 minút predchádzali a tretie sa denne o 12 minút oneskorovali. Jedného dňa odbíjali všetky hodiny dvanástu hodinu naraz. Za ako dlho to tak opäť bude? - Súčin 3 čísel
 Súčin 3 čísel je 42. Prvé je 1,5 krát väčšie ako druhé číslo a tretie je 3,5 krát väčšie ako druhé číslo. O ktoré čísla ide?
Súčin 3 čísel je 42. Prvé je 1,5 krát väčšie ako druhé číslo a tretie je 3,5 krát väčšie ako druhé číslo. O ktoré čísla ide? - Nákladné autá
 Dve nákladné autá vyšli z miest A, B proti sebe a po hodine sa stretli. Prvé auto prišlo do B o 27 minút neskôr ako druhé auto do A. Vypočítajte rýchlosť áut, ak vzdialenosť miest A, B je 90 km.
Dve nákladné autá vyšli z miest A, B proti sebe a po hodine sa stretli. Prvé auto prišlo do B o 27 minút neskôr ako druhé auto do A. Vypočítajte rýchlosť áut, ak vzdialenosť miest A, B je 90 km. - Materiál
 Materiál potrebný na stavbu by menšie auto priviezlo na 40-krát a väčšie na 30-krát. Keď prvé i druhé auto vykonalo 12 ciest, menšie auto odvolali a väčšie malo priviesť zvyšný materiál. Koľko ciest ešte musí urobiť väčšie auto?
Materiál potrebný na stavbu by menšie auto priviezlo na 40-krát a väčšie na 30-krát. Keď prvé i druhé auto vykonalo 12 ciest, menšie auto odvolali a väčšie malo priviesť zvyšný materiál. Koľko ciest ešte musí urobiť väčšie auto? - Cesta
 Na stavbu násypu cesty má voziť materiál 6 nákladných áut spolu 18 dní. Po troch dňoch bola poslaná na stavbu ešte 2 autá. Ako dlho celkom bude trvať navážanie materiálu?
Na stavbu násypu cesty má voziť materiál 6 nákladných áut spolu 18 dní. Po troch dňoch bola poslaná na stavbu ešte 2 autá. Ako dlho celkom bude trvať navážanie materiálu? - Automobilka
 V automobilke vyrobí teraz denne o 4 nové autá viac ako vlani, takže pri výrobe 360 automobilov sa ušetrí práve jeden celý pracovný deň. Koľko pracovných dní k výrobe 360 vozov potrebovali vlani?
V automobilke vyrobí teraz denne o 4 nové autá viac ako vlani, takže pri výrobe 360 automobilov sa ušetrí práve jeden celý pracovný deň. Koľko pracovných dní k výrobe 360 vozov potrebovali vlani? - Tri čísla
 Nájdi tri čísla tak, aby druhé číslo bolo 4 krát väčší ako prvé a tretie bolo o 5 menšie ako druhe číslo. Ich súčet je 67.
Nájdi tri čísla tak, aby druhé číslo bolo 4 krát väčší ako prvé a tretie bolo o 5 menšie ako druhe číslo. Ich súčet je 67.
