Hracie karty
Koľkými spôsobmi možno zamiešať 9 hracích kariet?
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Päť hostí
 Koľkými spôsobmi môžeme usadiť za stôl päť hostí, z ktorých dvaja sú manželia a chcú sedieť vedľa seba?
Koľkými spôsobmi môžeme usadiť za stôl päť hostí, z ktorých dvaja sú manželia a chcú sedieť vedľa seba? - Vlajky
 Koľko 4 farebných vlajok možno vytvoriť z 5 farieb tak, aby každá vlajka sa skladala z troch rôznych farieb?
Koľko 4 farebných vlajok možno vytvoriť z 5 farieb tak, aby každá vlajka sa skladala z troch rôznych farieb? - Koľkými 16
 Koľkými spôsobmi môže 10 áut zaparkovať vedľa seba na parkovisku?
Koľkými spôsobmi môže 10 áut zaparkovať vedľa seba na parkovisku? - Peter 21
 Peter, Jano, Alica a Rebeka išli na koncert vážnej hudby. Koľkými rôznými spôsobmi sa môžu usadiť na štyri voľné sedadlá ak Rebeka chce sedieť pri Janovi?
Peter, Jano, Alica a Rebeka išli na koncert vážnej hudby. Koľkými rôznými spôsobmi sa môžu usadiť na štyri voľné sedadlá ak Rebeka chce sedieť pri Janovi? - Marián
 Marián dostal v priebehu jedného dňa dve rôzne známky. Koľko je možností pre známky, ktoré mohol dostať?
Marián dostal v priebehu jedného dňa dve rôzne známky. Koľko je možností pre známky, ktoré mohol dostať? - V počítačovej
 V počítačovej hre je potrebné pozbierať v miestnosti 5 predmetov: meč, prsteň, obraz, kľúč a mincu. Záleží na poradí, v akom jednotlivé predmety pozbierame, pri zlom poradí prídeme o život . Koľko je všetkých poradí?
V počítačovej hre je potrebné pozbierať v miestnosti 5 predmetov: meč, prsteň, obraz, kľúč a mincu. Záleží na poradí, v akom jednotlivé predmety pozbierame, pri zlom poradí prídeme o život . Koľko je všetkých poradí? - S faktoriálom
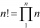 Vykráť výraz s faktoriálmi: 12! x 2 x 7! / 6 x 10! 8!
Vykráť výraz s faktoriálmi: 12! x 2 x 7! / 6 x 10! 8! - Koľkými 10
 Koľkými spôsobmi môže uložiť na poličku vedľa seba 7 rôznych kníh, keď kniha z matematiky musí byť na kraji police?
Koľkými spôsobmi môže uložiť na poličku vedľa seba 7 rôznych kníh, keď kniha z matematiky musí byť na kraji police? - Janka 7
 Janka si chce usporiadat na policku 4 anglicke a 3 slovenske knihy tak, aby boli zoradené najprv anglicke a potom slovenske knihy . Kolkymi sposobmi to moze urobit?
Janka si chce usporiadat na policku 4 anglicke a 3 slovenske knihy tak, aby boli zoradené najprv anglicke a potom slovenske knihy . Kolkymi sposobmi to moze urobit? - 8 ludi
 8 ľudí sedí za okrúhlym stolom. Koľkými spôsobmi ich možno posadiť okolo stola?
8 ľudí sedí za okrúhlym stolom. Koľkými spôsobmi ich možno posadiť okolo stola? - Na hokejovom 2
 Na hokejovom turnaji sa stretne 16 družstiev. Koľkými spôsobmi môže byť udelená zlatá, strieborná a bronzová medaila?
Na hokejovom turnaji sa stretne 16 družstiev. Koľkými spôsobmi môže byť udelená zlatá, strieborná a bronzová medaila? - Polohy kníh
 Koľko je polôh k uloženiu troch knih na poličku?
Koľko je polôh k uloženiu troch knih na poličku? - Päť písmen
 Koľkými spôsobmi je možné usporiadať päť písmen?
Koľkými spôsobmi je možné usporiadať päť písmen? - V skupine
 V skupine je 11 žiakov, medzi nimi práve jeden Martin. Koľko je všetkých možností na rozdanie 4 rôznych kníh týmto žiakom, ak každý z nich má dostať najviac jednu a Martin práve jednu z týchto kníh".
V skupine je 11 žiakov, medzi nimi práve jeden Martin. Koľko je všetkých možností na rozdanie 4 rôznych kníh týmto žiakom, ak každý z nich má dostať najviac jednu a Martin práve jednu z týchto kníh". - Telocvik
 Koľkými spôsobmi možno postaviť 20 žiakov do radu pri nástupe na telocvik?
Koľkými spôsobmi možno postaviť 20 žiakov do radu pri nástupe na telocvik? - Sedem 6
 Sedem spolužiačok chodí každý deň spolu na obed. Ak sa postavia do radu vždy v inom poradí, bude im stačiť školský rok, aby využili všetky možnosti?
Sedem spolužiačok chodí každý deň spolu na obed. Ak sa postavia do radu vždy v inom poradí, bude im stačiť školský rok, aby využili všetky možnosti? - Záhradník 2
 Záhradník má zasadiť 6 okrasných stromčekov. K dispozicií má 8 rozličných druhov stromov. Dva stromy A a B majú byť zasadené na ľavom okraji. Koľkými spôsobmi to môže záhradník spraviť, ak všetky zasadené stromčeky majú byť rôzne?
Záhradník má zasadiť 6 okrasných stromčekov. K dispozicií má 8 rozličných druhov stromov. Dva stromy A a B majú byť zasadené na ľavom okraji. Koľkými spôsobmi to môže záhradník spraviť, ak všetky zasadené stromčeky majú byť rôzne?
