MO Z9–I–2 - 2017
V lichobežníku VODY platí, že VO je dlhšou základňou, priesečník uhlopriečok K delí úsečku VD v pomere 3:2 a obsah trojuholníka KOV je rovný 13,5 cm2. Určte obsah celého lichobežníka.
Správna odpoveď:

Zobrazujem 8 komentárov:
Žiak
Mozem sa spytat, co znamenaju premenne k2, k3 a k4. Pripadne mozem poprosit o trochu podrobnejsi postup.
6 rokov 1 Like
Dr Math
k2,k3, k4 - koeficienty zvacsenia/ zmensenia; nieco ako rovnolahlosti. Koeficient zvacsenia/ zmensenia obsahu je druhou mocninou koeficientu zvacsenia/ zmensenia dlzky...
S1 je trojuholnik KOV
S2 je trojuholnik KDY
S3 je trojuholnik ODK
S4 je trojuholnik VKY
obsah trojuholnik je strana x vyska / 2. Napr. trojuholnik S3 = DYV - S2, a DYV ma k3-krat vacsiu vysku ako S2. atd
S1 je trojuholnik KOV
S2 je trojuholnik KDY
S3 je trojuholnik ODK
S4 je trojuholnik VKY
obsah trojuholnik je strana x vyska / 2. Napr. trojuholnik S3 = DYV - S2, a DYV ma k3-krat vacsiu vysku ako S2. atd
6 rokov 1 Like
Dr Math
este sme predsa nejaky nedostatok nasli a zmenili sme konecne riesenie... ale pointa ostava
6 rokov 1 Like
Žiak
Nedalo by sa to vyriesit cez spolocne vysky a podobnosti. Napr. Ze VOK a KOD. Vysku maju spolocnu a stranu x (uhlopriec. VD) ktora je 3ku2 tak aj obsah je 3ku2 t.j. 9 cm2. Sle neviem ako dalej dakujem za radu.
Tipy na súvisiace online kalkulačky
Potrebujete pomôcť spočítať, vykrátiť či vynásobiť zlomky? Skúste našu zlomkovú kalkulačku.
Vyskúšajte našu kalkulačka na prepočet pomeru.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte našu kalkulačka na prepočet pomeru.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Lichobežník
 V rovnoramennom lichobežníku KLMN je priesečník uhlopriečok označený písmenom S. Vypočítajte obsah lichobežníka, ak /KS/ :/SM/ = 2:1 a obsah trojuholníka KSN je 14 cm².
V rovnoramennom lichobežníku KLMN je priesečník uhlopriečok označený písmenom S. Vypočítajte obsah lichobežníka, ak /KS/ :/SM/ = 2:1 a obsah trojuholníka KSN je 14 cm². - Uhlopriečka lichobežníka
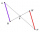 V lichobežníku ABCD sú dané dĺžky základní |AB| = 12 cm, |CD| = 8 cm. Bod S je priesečník uhlopriečok, pre ktorý platí |AS| = 6 cm. Vypočítaj dĺžku celej uhlopriečky AC.
V lichobežníku ABCD sú dané dĺžky základní |AB| = 12 cm, |CD| = 8 cm. Bod S je priesečník uhlopriečok, pre ktorý platí |AS| = 6 cm. Vypočítaj dĺžku celej uhlopriečky AC. - V lichobežníku
 V lichobežníku ABCD poznáme AB = 8 cm, výšku lichobežníka 6 cm a priesečník uhlopriečok je od AB vzdialený 4 cm. Vypočítaj obsah lichobežníka.
V lichobežníku ABCD poznáme AB = 8 cm, výšku lichobežníka 6 cm a priesečník uhlopriečok je od AB vzdialený 4 cm. Vypočítaj obsah lichobežníka. - Lichobežník
 V lichobežníku ABCD (AB||CD) platí |AB| = 15cm, |CD|=7cm, |AC|=12cm, AC je kolmé na BC. Aký obsah má lichobežník ABCD?
V lichobežníku ABCD (AB||CD) platí |AB| = 15cm, |CD|=7cm, |AC|=12cm, AC je kolmé na BC. Aký obsah má lichobežník ABCD? - Dôkaz - MO - C – I – 3
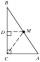 Päta výšky z vrcholu C v trojuholníku ABC delí stranu AB v pomere 1:2. Dokážte, že pri zvyčajnom označení dĺžok strán trojuholníka ABC platí nerovnosť 3|a-b| < c.
Päta výšky z vrcholu C v trojuholníku ABC delí stranu AB v pomere 1:2. Dokážte, že pri zvyčajnom označení dĺžok strán trojuholníka ABC platí nerovnosť 3|a-b| < c. - Základne 3
 Základne rovnoramenného lichobežníka ABCD majú dĺžky 10 cm a 6 cm. Jeho ramená zvierajú s dlhšou základňou uhol α = 50˚. Vypočítajte obvod a obsah lichobežníka ABCD.
Základne rovnoramenného lichobežníka ABCD majú dĺžky 10 cm a 6 cm. Jeho ramená zvierajú s dlhšou základňou uhol α = 50˚. Vypočítajte obvod a obsah lichobežníka ABCD. - Také tretinky
 Je daný lichobežníku ABCD s rovnobežnými stranami AB a CD pre bod E strany AB plati, že úsečka DE že delí lichobežník na dve časti s rovnakým obsahom. Spočítaj dĺžku úsečky AE.
Je daný lichobežníku ABCD s rovnobežnými stranami AB a CD pre bod E strany AB plati, že úsečka DE že delí lichobežník na dve časti s rovnakým obsahom. Spočítaj dĺžku úsečky AE. - Výška 20
 Výška v a základne a, c v lichobežníku ABCD sú v pomere 1 : 6 : 3, jeho obsah S = 324 cm štvorcových. Uhol pri vrchole B = 35 stupňov. Určte obvod lichobežníka
Výška v a základne a, c v lichobežníku ABCD sú v pomere 1 : 6 : 3, jeho obsah S = 324 cm štvorcových. Uhol pri vrchole B = 35 stupňov. Určte obvod lichobežníka - Vo všeobecnom
 Vo všeobecnom lichobežníku VLAK platí: |VL| = 5,5cm; |VK| = 3,5cm; |LK| = 4,8cm; |
Vo všeobecnom lichobežníku VLAK platí: |VL| = 5,5cm; |VK| = 3,5cm; |LK| = 4,8cm; | - Kvadratickej 44431
 1. V kartézskom rámci o funkciách f a g vieme, že: funkcia (f) je definovaná vzťahom f (x) = 2x², funkcia (g) je definovaná vzťahom g (x) = x + 3, bod (O) je začiatkom referencie, bod (C) je priesečník grafu funkcie (g ) s osou poradnice, body A a B sú pr
1. V kartézskom rámci o funkciách f a g vieme, že: funkcia (f) je definovaná vzťahom f (x) = 2x², funkcia (g) je definovaná vzťahom g (x) = x + 3, bod (O) je začiatkom referencie, bod (C) je priesečník grafu funkcie (g ) s osou poradnice, body A a B sú pr - MO - trojuholníky
 Na stranách AB a AC trojuholníka ABC leží postupne body E a F, na úsečke EF leží bod D. Přmky EF a BC sú rovnobežné a súčasne platí FD:DE = AE:EB = 2:1. Trojuholník ABC má obsah 27 hektárov a úsečkami EF, AD a DB je rozdelený na štyri časti. Určite obsahy
Na stranách AB a AC trojuholníka ABC leží postupne body E a F, na úsečke EF leží bod D. Přmky EF a BC sú rovnobežné a súčasne platí FD:DE = AE:EB = 2:1. Trojuholník ABC má obsah 27 hektárov a úsečkami EF, AD a DB je rozdelený na štyri časti. Určite obsahy - Úsečka 6
 Úsečka KL má dĺžku 12 cm. Bod X úsečku delí v pomere 1:5. Aká je dĺžka úsečky XL, ak bod X leží bližšie k bodu K?
Úsečka KL má dĺžku 12 cm. Bod X úsečku delí v pomere 1:5. Aká je dĺžka úsečky XL, ak bod X leží bližšie k bodu K? - Na úsečke
 Na úsečke AB s dĺžkou 15 cm leží bod C vzdialený od bodu A 4 cm. V akom pomere delí tento bod úsečku AB?
Na úsečke AB s dĺžkou 15 cm leží bod C vzdialený od bodu A 4 cm. V akom pomere delí tento bod úsečku AB? - Pravoúhlý lichobežník
 V pravouhlom lichobežníku ABCD platí: /AB/ = /BC/ = /AC/. Dĺžka strednej priečky je 6 cm. Vypočítaj obvod a obsah lichobežníka.
V pravouhlom lichobežníku ABCD platí: /AB/ = /BC/ = /AC/. Dĺžka strednej priečky je 6 cm. Vypočítaj obvod a obsah lichobežníka. - Kosoštvorec 44
 Kosoštvorec KLMN má obvod 32 cm a priesečník jeho uhlopriéčok je od strany LM vzdialený 3 cm. Aký je obsah kosoštvorca?
Kosoštvorec KLMN má obvod 32 cm a priesečník jeho uhlopriéčok je od strany LM vzdialený 3 cm. Aký je obsah kosoštvorca? - Lichobežník
 Daný je lichobežník ABCD so základňami AB, CD. Nech K je stred strany AB a L je stred strany CD. Obsah trojuholníka ALB je 15 cm² a obsah trojuholníka DKC je 10 cm². Vypočítajte obsah lichobežníka ABCD.
Daný je lichobežník ABCD so základňami AB, CD. Nech K je stred strany AB a L je stred strany CD. Obsah trojuholníka ALB je 15 cm² a obsah trojuholníka DKC je 10 cm². Vypočítajte obsah lichobežníka ABCD. - Štvorce
 Na dvoma stranami trojuholníka ABC sú zostrojené štvorce. Obsah štvorca nad stranou BC je 25 cm². Veľkosť výšky vc na stranu AB je 3 cm. Pata P výšky vc delí stranu AB v pomere 2:1. Strana AC je dlhšia ako strana BC. Vypočítajte v cm dĺžku strany AB. Vypo
Na dvoma stranami trojuholníka ABC sú zostrojené štvorce. Obsah štvorca nad stranou BC je 25 cm². Veľkosť výšky vc na stranu AB je 3 cm. Pata P výšky vc delí stranu AB v pomere 2:1. Strana AC je dlhšia ako strana BC. Vypočítajte v cm dĺžku strany AB. Vypo
