MO Z6 I-3 2017 fľaše
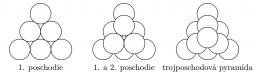
Jano mal 100 rovnakých zaváracích fliaš, z ktorých si staval trojboké pyramídy. Najvyššie poschodie pyramídy má vždy jednu fľašu, druhé poschodie zhora predstavuje rovnostranný trojuholník, ktorého strana pozostáva z dvoch fliaš, atď. Príklad konštrukcie trojposchodovej pyramídy je na obrázku.
1. Koľko fliaš Jano potreboval na päťposchodovú pyramídu?
2. Koľko poschodí mala pyramída, na ktorú bolo použitých čo najviac Janových fliaš?
1. Koľko fliaš Jano potreboval na päťposchodovú pyramídu?
2. Koľko poschodí mala pyramída, na ktorú bolo použitých čo najviac Janových fliaš?
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Cukor - kváder
 Pejko dostal od svojho pána kváder zložený z navzájom rovnakých kociek cukru, ktorých bolo najmenej 1000 a najviac 2000. Pejko kocky cukru odjedal po jednotlivých vrstvách-prvý deň odjedol jednu vrstvu spredu,druhý deň jednu vrstvu sprava a tretí deň jedn
Pejko dostal od svojho pána kváder zložený z navzájom rovnakých kociek cukru, ktorých bolo najmenej 1000 a najviac 2000. Pejko kocky cukru odjedal po jednotlivých vrstvách-prvý deň odjedol jednu vrstvu spredu,druhý deň jednu vrstvu sprava a tretí deň jedn - Zvláštne hodinky
 Fero si na blšom trhu kúpil zvláštne hodinky. Majú len jednu ručičku (minútovú) a číselník, na ktorom sa zobrazuje, aký uhol by práve zvierala hodinová a minútová ručička. Koľko bolo hodín, keď sa na jeho hodinkách objavilo to, čo vidíš na obrázku - minút
Fero si na blšom trhu kúpil zvláštne hodinky. Majú len jednu ručičku (minútovú) a číselník, na ktorom sa zobrazuje, aký uhol by práve zvierala hodinová a minútová ručička. Koľko bolo hodín, keď sa na jeho hodinkách objavilo to, čo vidíš na obrázku - minút - Spotreboval 8127
 Na tri rovnaké diely plotu pribil otec 54 tyčiek. Koľko tyčiek potreboval celkom na plot, ktorý mal 10 rovnakých dielov a bránku, na ktorú spotreboval otec ešte 10 tyčiek?
Na tri rovnaké diely plotu pribil otec 54 tyčiek. Koľko tyčiek potreboval celkom na plot, ktorý mal 10 rovnakých dielov a bránku, na ktorú spotreboval otec ešte 10 tyčiek? - Spotreboval 3011
 Na 3 rovnaké diely plotu pribil oteckov 54 tyčiek. Koľko tyčiek potreboval celkom na plot, ktorý mal 10 rovnakých dielov a bránku, na ktorú spotreboval ešte 10 tyčiek?
Na 3 rovnaké diely plotu pribil oteckov 54 tyčiek. Koľko tyčiek potreboval celkom na plot, ktorý mal 10 rovnakých dielov a bránku, na ktorú spotreboval ešte 10 tyčiek? - Inteligenčný test
 Paľo, Jano, Karol a Rišo robili inteligenčný test. Paľo správne odpovedal na polovicu otázok plus 7 otázok, Jano na tretinu plus 18 otázok, Karol na štvrtinu plus 21 otázok a Rišo na pätinu plus 25 otázok. Karol po teste povedal:,, Mám pocit, ze sa mi cel
Paľo, Jano, Karol a Rišo robili inteligenčný test. Paľo správne odpovedal na polovicu otázok plus 7 otázok, Jano na tretinu plus 18 otázok, Karol na štvrtinu plus 21 otázok a Rišo na pätinu plus 25 otázok. Karol po teste povedal:,, Mám pocit, ze sa mi cel - Na očislovanie
 Na očíslovanie hrubej knihy bolo použitých 1533 číslic. Koľko strán má tato kniha, ak je očíslovaná každá strana vrátane strany 1?
Na očíslovanie hrubej knihy bolo použitých 1533 číslic. Koľko strán má tato kniha, ak je očíslovaná každá strana vrátane strany 1? - Pyramída v Gize
 Veľká pyramída v Gize má tvar pravidelného štvorbokého ihlana. Podstavná hrana má dľžku 227 m a výška pyramídy je 140 m. Akú hmotnosť má kameň, ktorý bol potrebný na stavbu tejto pyramídy, ak hmotnosť 1 m³ kameňa je 2,5 t?
Veľká pyramída v Gize má tvar pravidelného štvorbokého ihlana. Podstavná hrana má dľžku 227 m a výška pyramídy je 140 m. Akú hmotnosť má kameň, ktorý bol potrebný na stavbu tejto pyramídy, ak hmotnosť 1 m³ kameňa je 2,5 t? - Mrakodrap
 Obyvateľ mrakodrapu si zaparkoval svoje auto v podzemnej garáži označenej tlačidlami vo výťahu číslom -3. Vyviezol sa na svoje poschodie označené číslom 26. Koľko poschodí sa viezol vo výťahu ?
Obyvateľ mrakodrapu si zaparkoval svoje auto v podzemnej garáži označenej tlačidlami vo výťahu číslom -3. Vyviezol sa na svoje poschodie označené číslom 26. Koľko poschodí sa viezol vo výťahu ? - Najväčšia 2
 Najväčšia egyptská pyramída má tvar pravidelného štvorbokého ihlana s hranou podstavy približne 227 metrov a výškou asi 140 metrov. Koľko ton kameňa prepravili robotníci na jej stavbu? 1 kubík kameňa má hmotnosť 2 500 kg a chodby a miestnosti vo vnútri py
Najväčšia egyptská pyramída má tvar pravidelného štvorbokého ihlana s hranou podstavy približne 227 metrov a výškou asi 140 metrov. Koľko ton kameňa prepravili robotníci na jej stavbu? 1 kubík kameňa má hmotnosť 2 500 kg a chodby a miestnosti vo vnútri py - Pán Peter
 Pán Peter potrebuje na svojom pozemku vyhĺbiť studňu hlbokú 20 m. Firma AZET účtuje za prvý meter 1 euro a za každý nasledujúci 2 krát viac. Firma ZETA účtuje za každý meter hĺbky studne 200 eur. Ktorú firmu si má pán Peter vybrať, ak chce čo najviac ušet
Pán Peter potrebuje na svojom pozemku vyhĺbiť studňu hlbokú 20 m. Firma AZET účtuje za prvý meter 1 euro a za každý nasledujúci 2 krát viac. Firma ZETA účtuje za každý meter hĺbky studne 200 eur. Ktorú firmu si má pán Peter vybrať, ak chce čo najviac ušet - Korytnačom 25571
 Na Korytnačom ostrove je neobyvklé počasie. V pondelok av stredu vždy prší, v sobotu je hmla a ostatné dni svieti slniečko. Skupinka turistov chce na ostrov prísť na 44-dňovú dovolenku. Ktorý deň by mala dovolenka začať, aby si užili čo najviac slnečných
Na Korytnačom ostrove je neobyvklé počasie. V pondelok av stredu vždy prší, v sobotu je hmla a ostatné dni svieti slniečko. Skupinka turistov chce na ostrov prísť na 44-dňovú dovolenku. Ktorý deň by mala dovolenka začať, aby si užili čo najviac slnečných - Marienka - mo
 Marienka rozmiestni do vrcholov pravidelného osemuholníka rôzne počty od jedného po osem cukríkov. Peter si potom môže vybrať, ktoré tri kôpky cukríkov dá Marienke, ostatné si ponechá. Jedinou podmienkou je, že tieto tri kôpky ležia vo vrcholoch rovnorame
Marienka rozmiestni do vrcholov pravidelného osemuholníka rôzne počty od jedného po osem cukríkov. Peter si potom môže vybrať, ktoré tri kôpky cukríkov dá Marienke, ostatné si ponechá. Jedinou podmienkou je, že tieto tri kôpky ležia vo vrcholoch rovnorame - Automat na fľaše
 Jeden automat na fľaše uzatvorí za minútu 60 zaváracích fliaš, druhý za rovnaký čas o 20 fliaš menej. Za koľko minút uzavrú obidva automaty 900 fliaš, ak budú uvedené do chodu súčasne.
Jeden automat na fľaše uzatvorí za minútu 60 zaváracích fliaš, druhý za rovnaký čas o 20 fliaš menej. Za koľko minút uzavrú obidva automaty 900 fliaš, ak budú uvedené do chodu súčasne. - Červených 6118
 Peter si vybral guličky dvoch farieb. Koľko ktorých mal ak počty žltých a červených boli v pomere 7 : 5 a žltých bolo o šesť viac?
Peter si vybral guličky dvoch farieb. Koľko ktorých mal ak počty žltých a červených boli v pomere 7 : 5 a žltých bolo o šesť viac? - Štvorizbových 82265
 V jednom panelovom dome je 13 poschodí a 7 vchodov. V každom vchode sú v každom z deviatich poschodí 2 trojizbové a 1 dvojizbový byt, vo zvyšných štyroch poschodiach je na každom poschodí vždy 1 štvorizbový a 2 dvoch izbové byty. Vypočítajte, koľko je v t
V jednom panelovom dome je 13 poschodí a 7 vchodov. V každom vchode sú v každom z deviatich poschodí 2 trojizbové a 1 dvojizbový byt, vo zvyšných štyroch poschodiach je na každom poschodí vždy 1 štvorizbový a 2 dvoch izbové byty. Vypočítajte, koľko je v t - Ako budeme
 Ako budeme volať jednu časť, keď celok rozdelíme na 5(6,7,8,9,10) rovnakých častí?
Ako budeme volať jednu časť, keď celok rozdelíme na 5(6,7,8,9,10) rovnakých častí? - Pyramída
 Nájdite celkový povrch obdĺžnikovej pyramídy, ak má je vysoká 8 dm a základňa je 10 dm x 6 dm.
Nájdite celkový povrch obdĺžnikovej pyramídy, ak má je vysoká 8 dm a základňa je 10 dm x 6 dm.
