Z7-I-5 MO 2017
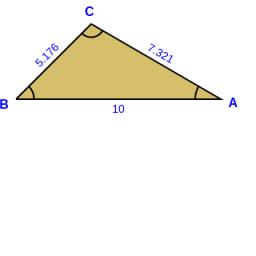
Prokop zostrojil trojuholník ABC, ktorého vnútorný uhol pri vrchole A bol väčší ako 60° a vnútorný uhol pri vrchole B bol menší ako 60°. Juraj narysoval v polrovine určenej priamkou AB a bodom C bod D, a to tak, že trojuholník ABD bol rovnostranný. Potom chlapci zistili, že trojuholníky ACD a BCD sú rovnoramenné s hlavným vrcholom D. Určte veľkosť uhla ACB.
Správna odpoveď:
Zobrazujem 4 komentáre:
Euklides
Toto je analyticko-algebraické řešení, kdy za neznámé úhly dosadíte proměnné x,y,z, dosadíte si je do rovnic dle známého pravidla, že součet vnitřních úhlů trojúhelníku je 180° a vyřešíte soustavu rovnic. Dostanete výsledek - 30°
Zajímavější je zamyslet se nad tím, proč je to VŹDY právě 30°
A tady je mnohem názornější geometrické řešení přes středové a obvodové úhly kružnice.
Sestrojte rovnoramenný trojúhelník ABD a kružnici se středem v bodu D procházející body A i B.
Jako bod C si zvolte jakýkoliv bod na kružnici (v polorovinně dané přímkou AB a bodem D).
Jelikož úhel ACB (který máme určit) je obvodovým úhlem ke středovému úhlu ADB (a ten je 60° z definice rovnostrannosti tohoto trojúhelníku), jeho velikost je přesně jeho polovinou. A to VŽDY, nezávisle na tom, kde se bod C na kružnici nachází.
Nakreslete si, je to pak vidět lépe než ze soustavy rovnic.
Zajímavější je zamyslet se nad tím, proč je to VŹDY právě 30°
A tady je mnohem názornější geometrické řešení přes středové a obvodové úhly kružnice.
Sestrojte rovnoramenný trojúhelník ABD a kružnici se středem v bodu D procházející body A i B.
Jako bod C si zvolte jakýkoliv bod na kružnici (v polorovinně dané přímkou AB a bodem D).
Jelikož úhel ACB (který máme určit) je obvodovým úhlem ke středovému úhlu ADB (a ten je 60° z definice rovnostrannosti tohoto trojúhelníku), jeho velikost je přesně jeho polovinou. A to VŽDY, nezávisle na tom, kde se bod C na kružnici nachází.
Nakreslete si, je to pak vidět lépe než ze soustavy rovnic.
Tipy na súvisiace online kalkulačky
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Vypočet rovnoramenného trojuholníka.
Vypočet rovnostranného trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vypočet rovnoramenného trojuholníka.
Vypočet rovnostranného trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- geometria
- priamka
- stredový a obvodový uhol
- algebra
- rovnica
- vyjadrenie neznámej zo vzorca
- planimetria
- trojuholník
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- MO z9 2022
 Sú dané dva zhodné rovnostranné trojuholníky ABC a BDE tak, že veľkosť uhla ABD je väčšia ako 120° a menšia ako 180° a body C, E ležia v rovnakej polrovine vymedzenej priamkou AD. Priesečník CD a AE je označený F. Určte veľkosť uhla AFD.
Sú dané dva zhodné rovnostranné trojuholníky ABC a BDE tak, že veľkosť uhla ABD je väčšia ako 120° a menšia ako 180° a body C, E ležia v rovnakej polrovine vymedzenej priamkou AD. Priesečník CD a AE je označený F. Určte veľkosť uhla AFD. - Hlavný vrchol
 ABC je rovnoramenný trojuholník so základňou BC a hlavným vrcholom A. Uhol pri vrchole A má veľkosť 18°. Akú veľkosť bude mať uhol pri vrchole B?
ABC je rovnoramenný trojuholník so základňou BC a hlavným vrcholom A. Uhol pri vrchole A má veľkosť 18°. Akú veľkosť bude mať uhol pri vrchole B? - MO Z7–I–6 2021
 V trojuholníku ABC leží na strane AC bod D a na strane BC bod E. Veľkosti uhlov ABD, BAE, CAE a CBD sú postupne 30°, 60°, 20° a 30°. určte veľkosť uhla AED.
V trojuholníku ABC leží na strane AC bod D a na strane BC bod E. Veľkosti uhlov ABD, BAE, CAE a CBD sú postupne 30°, 60°, 20° a 30°. určte veľkosť uhla AED. - MO Z9 2019 domáce kolo
 V trojuholníku ABC leží bod P v tretine úsečky AB (bližšie bodu A), bod R je v tretine úsečky PB (bližšie bodu P) a bod Q leží na úsečke BC tak, že uhly PCB a RQB sú zhodné. Určte pomer obsahov trojuholníkov ABC a PQC.
V trojuholníku ABC leží bod P v tretine úsečky AB (bližšie bodu A), bod R je v tretine úsečky PB (bližšie bodu P) a bod Q leží na úsečke BC tak, že uhly PCB a RQB sú zhodné. Určte pomer obsahov trojuholníkov ABC a PQC.
- Body ABC
 Body ABC ležia na kružnici k(S, r) tak, že uhol pri B je tupý. Aký veľký musí byť uhol pri vrchole B štvoruholníka SCBA, aby bol tento uhol trikrát väčší ako vnútorný uhol ASC toho istého štvoruholníka?
Body ABC ležia na kružnici k(S, r) tak, že uhol pri B je tupý. Aký veľký musí byť uhol pri vrchole B štvoruholníka SCBA, aby bol tento uhol trikrát väčší ako vnútorný uhol ASC toho istého štvoruholníka? - Vnútorné uhly 7
 Veľkosť vnútorného uhla pri hlavnom vrchole C rovnoramenného trojuholníka ABC je 72°. Priamka p, rovnobežná so základňou tohto trojuholníka, rozdeľuje trojuholník na lichobežník a menší trojuholník. Aké veľké sú vnútorné uhly lichobežníka?
Veľkosť vnútorného uhla pri hlavnom vrchole C rovnoramenného trojuholníka ABC je 72°. Priamka p, rovnobežná so základňou tohto trojuholníka, rozdeľuje trojuholník na lichobežník a menší trojuholník. Aké veľké sú vnútorné uhly lichobežníka? - Uhly v trojuholníku
 V trojuholníku ABC je vnútorný uhol pri vrchole C dvakrát väčší ako vnútorný uhol pri vrchole A. Vonkajší uhol pri vrchole B meria 117°. Aký veľký je vonkajší uhol pri vrchole A?
V trojuholníku ABC je vnútorný uhol pri vrchole C dvakrát väčší ako vnútorný uhol pri vrchole A. Vonkajší uhol pri vrchole B meria 117°. Aký veľký je vonkajší uhol pri vrchole A? - Vnútorné uhly
 Určte vnútorné uhly trojuholníka ABC, ak uhol pri vrchole C je dvakrát väčší ako uhol pri vrchole B a uhol pri vrchole B je o 4 stupne menší ako uhol pri vrchole A.
Určte vnútorné uhly trojuholníka ABC, ak uhol pri vrchole C je dvakrát väčší ako uhol pri vrchole B a uhol pri vrchole B je o 4 stupne menší ako uhol pri vrchole A. - Päťuholník
 Vo vnútri pravidelného päťuholníka ABCDE je bod P taký, že trojuholník ABP je rovnostranný. Aký veľký je uhol BCP? Urob si náčrtok.
Vo vnútri pravidelného päťuholníka ABCDE je bod P taký, že trojuholník ABP je rovnostranný. Aký veľký je uhol BCP? Urob si náčrtok.
- Trojuholníka 81613
 V rovine je umiestnený trojuholník ABC s pravým uhlom pri vrchole C, pre ktorý platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určite hodnotu x b) určite súradnice bodu M, ktorý je stredom úsečky AB c) dokážte že vektory AB a CM sú kolmé d) určite v
V rovine je umiestnený trojuholník ABC s pravým uhlom pri vrchole C, pre ktorý platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určite hodnotu x b) určite súradnice bodu M, ktorý je stredom úsečky AB c) dokážte že vektory AB a CM sú kolmé d) určite v - Zostroj 8
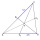 Zostroj trojuholník ABC, ak je dané: veľkosť strany AC je 6 cm, veľkosť uhla ACB je 60° a vzdialenosť ťažiska T od vrcholu A je 4 cm. (Náčrt, rozbor, zápis konštrukcie, konštrukcia)
Zostroj trojuholník ABC, ak je dané: veľkosť strany AC je 6 cm, veľkosť uhla ACB je 60° a vzdialenosť ťažiska T od vrcholu A je 4 cm. (Náčrt, rozbor, zápis konštrukcie, konštrukcia) - Uhly
 Vonkajší uhol trojuholníka ABC pri vrchole A je 114°12'. Vonkajší uhol pri vrchole B je 139°18'. Akú veľkosť má vnútorný uhol pri vrchole C?
Vonkajší uhol trojuholníka ABC pri vrchole A je 114°12'. Vonkajší uhol pri vrchole B je 139°18'. Akú veľkosť má vnútorný uhol pri vrchole C? - Štvoruholník 13
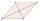 Štvoruholník ABCD je súmerný podľa uhlopriečky AC. Dĺžka AC je 12 cm, dĺžka BC je 6 cm a vnútorný uhol pri vrchole B je pravý. na stranách AB, AD sú dané body E, F tak, že trojuholník ECF je rovnostranný. Určite dĺžku úsečky EF.
Štvoruholník ABCD je súmerný podľa uhlopriečky AC. Dĺžka AC je 12 cm, dĺžka BC je 6 cm a vnútorný uhol pri vrchole B je pravý. na stranách AB, AD sú dané body E, F tak, že trojuholník ECF je rovnostranný. Určite dĺžku úsečky EF. - Kosodĺžnik - uhlopriečka
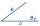 V kosodĺžniku sú rozmery strán a=5cm, b=6 cm a veľkosť uhla pri vrchole A je 60°. Aká je dĺžka strany AC?
V kosodĺžniku sú rozmery strán a=5cm, b=6 cm a veľkosť uhla pri vrchole A je 60°. Aká je dĺžka strany AC?
- Uhly
 V trojuholníku ABC je vnútorný uhol pri vrchole B o 10 stupňov väčší ako uhol pri vrchole A a uhol pri vrchole C je trikrát väčší ako uhol pri vrchole B. Vypočítajte veľkosti vnútorných uhlov trojuholníka.
V trojuholníku ABC je vnútorný uhol pri vrchole B o 10 stupňov väčší ako uhol pri vrchole A a uhol pri vrchole C je trikrát väčší ako uhol pri vrchole B. Vypočítajte veľkosti vnútorných uhlov trojuholníka. - Rovnoramennom 23271
 V rovnoramennom trojuholníku je veľkosť uhla pri hlavnom vrchole o 20° menšia ako dvojnásobná veľkosť uhla pri základni. Aké sú vnútorné uhly trojuholníka?
V rovnoramennom trojuholníku je veľkosť uhla pri hlavnom vrchole o 20° menšia ako dvojnásobná veľkosť uhla pri základni. Aké sú vnútorné uhly trojuholníka? - Rovnoramenný lichobežník
 Je daný rovnoramenný lichobežník ABCD, v ktorom platí: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: Na jeho strane BC je bod K taký, že |BK| = 2 |KC|, na jeho strane CD je bod L taký, že |CL| = 2 |LD|, a na jeho strane DA je bod M taký, že |DM| = 2 |MA|. Určte veľkos
Je daný rovnoramenný lichobežník ABCD, v ktorom platí: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: Na jeho strane BC je bod K taký, že |BK| = 2 |KC|, na jeho strane CD je bod L taký, že |CL| = 2 |LD|, a na jeho strane DA je bod M taký, že |DM| = 2 |MA|. Určte veľkos
