Výslednica 3
Dve sily F1=580N a F2=630N zvierajú uhol 59 stupňov. Vypočítajte ich výslednicu F.
Správna odpoveď:
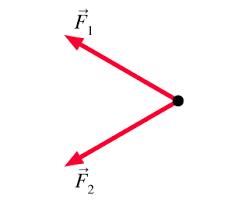
Zobrazujem 1 komentár:
Dr Math
Pre zaujmecov sme pripravili kalkulacku na scitanie dvoch vektorov:
https://www.hackmath.net/sk/kalkulacka/sucet-vektorov?what=&a=580&a1=59&b=630&submit=Vyrie%C5%A1
je to dost podobne ako SUS trojuholnik, akurat sa neriesi strana ale uhlopriecka rovnobeznika
https://www.hackmath.net/sk/kalkulacka/sucet-vektorov?what=&a=580&a1=59&b=630&submit=Vyrie%C5%A1
je to dost podobne ako SUS trojuholnik, akurat sa neriesi strana ale uhlopriecka rovnobeznika
Tipy na súvisiace online kalkulačky
Dva vektory určené veľkosťami a vzájomným uhlom sčíta naša kalkulačka sčítania vektorov.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Zvierajú 67664
 Sila R = 12 N sa má rozdeliť na dve zložky F1, F2, ich smery zvierajú so smerom sily R uhlami α = 30°, β = 45°. Aké sú zložky F1, F2?
Sila R = 12 N sa má rozdeliť na dve zložky F1, F2, ich smery zvierajú so smerom sily R uhlami α = 30°, β = 45°. Aké sú zložky F1, F2? - Dve cesty
 Dve priame cesty sa križujú a zvierajú uhol alfa= 53 stupňov 30'. Na jednej z nich stoja dva stĺpy, jeden na križovatke, druhý vo vzdialenosti 500m od nej. Ako ďaleko treba ist od križovatky po druhej ceste, aby sme videli obidva stĺpy v zornom uhle beta?
Dve priame cesty sa križujú a zvierajú uhol alfa= 53 stupňov 30'. Na jednej z nich stoja dva stĺpy, jeden na križovatke, druhý vo vzdialenosti 500m od nej. Ako ďaleko treba ist od križovatky po druhej ceste, aby sme videli obidva stĺpy v zornom uhle beta? - Hmotný bod
 Na hmotný bod pôsobia dve rovnaké sily o veľkosti 30 N. Určte veľkosť výslednica, zvierajú ak tieto sily uhol 42°.
Na hmotný bod pôsobia dve rovnaké sily o veľkosti 30 N. Určte veľkosť výslednica, zvierajú ak tieto sily uhol 42°. - Pole
 Pole má tvar rovnobežníka s rozmermi a=80 m a prislúchajúcou výškou 296 m. Dve a dve strany zvierajú uhol 80°. Vypočítajte výmeru pola v hektároch.
Pole má tvar rovnobežníka s rozmermi a=80 m a prislúchajúcou výškou 296 m. Dve a dve strany zvierajú uhol 80°. Vypočítajte výmeru pola v hektároch.
- Výslednica síl
 Sily o veľkostiach F1 = 42N a F2 = 35N pôsobia v spoločnom bode a zvierajú uhol s veľkosťou 77° 12'. Ako veľká je ich výslednica?
Sily o veľkostiach F1 = 42N a F2 = 35N pôsobia v spoločnom bode a zvierajú uhol s veľkosťou 77° 12'. Ako veľká je ich výslednica? - Päťboký ihlan
 Vypočítajte objem pravidelného 5-bokého ihlana ABCDEV, ak |AB|= 7,8 cm a roviny ABV , ABC zvierajú uhol 29 stupňov.
Vypočítajte objem pravidelného 5-bokého ihlana ABCDEV, ak |AB|= 7,8 cm a roviny ABV , ABC zvierajú uhol 29 stupňov. - 100 percent
 Koľko je 100 %, ak 44 % je 632?
Koľko je 100 %, ak 44 % je 632? - Sily
 Na bod O pôsobia tri navzájom kolmé sily F1=20 N, F2=7 N, F3=19 N. Určte výslednicu F a uhly, ktoré zviera výslednica so zložkami F1, F2, F3.
Na bod O pôsobia tri navzájom kolmé sily F1=20 N, F2=7 N, F3=19 N. Určte výslednicu F a uhly, ktoré zviera výslednica so zložkami F1, F2, F3. - Výslednica síl
 Vypočítajte matematicky a graficky výslednicu sústavy troch síl so spoločným pôsobiskom, ak: F1 = 50kN α1 = 30° F2 = 40kN α2 = 45° F3 = 40kN α3 = 25°
Vypočítajte matematicky a graficky výslednicu sústavy troch síl so spoločným pôsobiskom, ak: F1 = 50kN α1 = 30° F2 = 40kN α2 = 45° F3 = 40kN α3 = 25°
- V trojuholníku
 V trojuholníku ABC sa veľkosť vnútorného uhla gama rovná tretine vnútorného uhla alfa. Veľkosť vnútorného uhla beta je o 80 stupňov väčší ako veľkosť uhla gama. Vypočítajte veľkosti vnútorných uhlov trojuholníka ABC.
V trojuholníku ABC sa veľkosť vnútorného uhla gama rovná tretine vnútorného uhla alfa. Veľkosť vnútorného uhla beta je o 80 stupňov väčší ako veľkosť uhla gama. Vypočítajte veľkosti vnútorných uhlov trojuholníka ABC. - Denny 3
 Denný normovaný výkon pracovníka predpokladá vyrobenie 530 súčiastok rovnakého druhu. Skutočný výkon pracovníka bol 659 ks. Uvedte na koľko % pracovník splnil plán.
Denný normovaný výkon pracovníka predpokladá vyrobenie 530 súčiastok rovnakého druhu. Skutočný výkon pracovníka bol 659 ks. Uvedte na koľko % pracovník splnil plán. - Narysujte: 2511
 Narysujte kružnicu k/S 4,5 cm/. Ďalej narysujte: a/dva navzájom kolmé priemery AB a CD b/dva polomery SA a SE, ktoré zvierajú uhol 75 stupňov c/tetiva /KL/= 4 cm d/tetiva /MN/, ktorá je kolmá ku KL
Narysujte kružnicu k/S 4,5 cm/. Ďalej narysujte: a/dva navzájom kolmé priemery AB a CD b/dva polomery SA a SE, ktoré zvierajú uhol 75 stupňov c/tetiva /KL/= 4 cm d/tetiva /MN/, ktorá je kolmá ku KL - Ozubené kolesá
 Dve ozubené kolesá, ktoré do seba zapadajú majú počet zubov z1=109 a z2=165. Vypočítajte otáčky prvého kolesa, ak druhé koleso sa otáča 506 otáčok za minútu.
Dve ozubené kolesá, ktoré do seba zapadajú majú počet zubov z1=109 a z2=165. Vypočítajte otáčky prvého kolesa, ak druhé koleso sa otáča 506 otáčok za minútu. - Tri vektory
 Tri sily, ktorých veľkosti sú v pomere 9:10:17, pôsobia v rovine v jednom bode tak, že sú v rovnováhe. Určte veľkosti uhlov, ktoré zvierajú každé dve sily
Tri sily, ktorých veľkosti sú v pomere 9:10:17, pôsobia v rovine v jednom bode tak, že sú v rovnováhe. Určte veľkosti uhlov, ktoré zvierajú každé dve sily
- Skalárny súčin
 Vypočítajte skalárny súčin vektorov u a v keď |u|=5, |v|=2 a keď vektory u, v, zvierajú uhol: a) 60° b) 45° c) 120°
Vypočítajte skalárny súčin vektorov u a v keď |u|=5, |v|=2 a keď vektory u, v, zvierajú uhol: a) 60° b) 45° c) 120° - Zostrojte
 Zostrojte trojuholník ABC, ak poznáte dĺžky jeho strán c = 5 cm, a = 4 cm a uhol ABC má ve¾kosť 60°. Odmerajte dĺžku strany b v milimetroch. Dĺžka strany b je: a, 75 mm < b < 81 mm b, 53 mm < b < 59 mm c, 43 mm < b < 49 mm d, 13 mm <
Zostrojte trojuholník ABC, ak poznáte dĺžky jeho strán c = 5 cm, a = 4 cm a uhol ABC má ve¾kosť 60°. Odmerajte dĺžku strany b v milimetroch. Dĺžka strany b je: a, 75 mm < b < 81 mm b, 53 mm < b < 59 mm c, 43 mm < b < 49 mm d, 13 mm < - Pre súčet
 Pre súčet s veľkostí vnútorných uhlov mnohouholníka, kde n je počet jeho strán, platí vzťah s=(n−2)⋅180 stupňov. Koľko strán má mnohouholník, ak súčet veľkostí jeho vnútorných uhlov je 900°?
Pre súčet s veľkostí vnútorných uhlov mnohouholníka, kde n je počet jeho strán, platí vzťah s=(n−2)⋅180 stupňov. Koľko strán má mnohouholník, ak súčet veľkostí jeho vnútorných uhlov je 900°?
