Do rovnostranného
Do rovnostranného trojuholníka so stranou 10 cm je vpísaný štvorec. Vypočítaj dlžku strany štvorca.
Správna odpoveď:
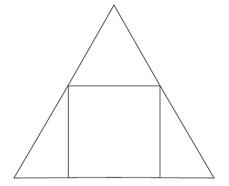
Tipy na súvisiace online kalkulačky
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Vypočet rovnostranného trojuholníka.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vypočet rovnostranného trojuholníka.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Polovica obĺžnika
 Vypočítajte obsah pravouhlého trojuholníka ABC s odvesnami a=15cm, b=1,7dm.
Vypočítajte obsah pravouhlého trojuholníka ABC s odvesnami a=15cm, b=1,7dm. - Výška, uhol a strana
 Vypočítajte obsah trojuholníka ABC, v ktorom poznáte stranu c=5 cm, uhol pri vrchole A= 70 stupňov a pomer úsekov, ktoré vytína výška na stranu c je 1:3.
Vypočítajte obsah trojuholníka ABC, v ktorom poznáte stranu c=5 cm, uhol pri vrchole A= 70 stupňov a pomer úsekov, ktoré vytína výška na stranu c je 1:3. - Obvod 58
 Obvod štvobokého ihlava je 48 m a jeho výška ja 2,5m; koľko bude stáť plech na tento ihlan, keď 1m² stojí 1,5€; do plochy sa počíta aj 12% strata na spoje a záhyby.
Obvod štvobokého ihlava je 48 m a jeho výška ja 2,5m; koľko bude stáť plech na tento ihlan, keď 1m² stojí 1,5€; do plochy sa počíta aj 12% strata na spoje a záhyby. - Rovnoramenný trojuholník -VU
 Vypočítajte dĺžky strán v rovnoramennom trojuholníku, ak je dana výška (na základňu) Vc= 8,8cm a uhol pri zakladni alfa= 38°40`.
Vypočítajte dĺžky strán v rovnoramennom trojuholníku, ak je dana výška (na základňu) Vc= 8,8cm a uhol pri zakladni alfa= 38°40`. - Zastroj
 Zastroj rovnoramenný trojuholník ABY zo základňou AB dĺžky 5 cm a uhlom pri hlavnom vrchole veľkosti 50°. Zapíše postup konštrukcie.
Zastroj rovnoramenný trojuholník ABY zo základňou AB dĺžky 5 cm a uhlom pri hlavnom vrchole veľkosti 50°. Zapíše postup konštrukcie. - Tetiva - uhol
 Je daná kružnica k so stredom v bode S a polomerom 6 cm. Vypočítaj veľkosť stredového uhla, ktorý patí tetive dlhej 10 cm.
Je daná kružnica k so stredom v bode S a polomerom 6 cm. Vypočítaj veľkosť stredového uhla, ktorý patí tetive dlhej 10 cm. - Obsah 44
 Obsah pravouhlému trojuholníka ABC je 346 cm² a uhol pri vrchole A je 64°. Vypočítajte dĺžky odvesien a, b.
Obsah pravouhlému trojuholníka ABC je 346 cm² a uhol pri vrchole A je 64°. Vypočítajte dĺžky odvesien a, b. - Ťažnice v PT
 V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku.
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku. - Daný je 9
 Daný je rovnoramenný trojuholník, ktorého základňa je 8cm a ramená majú dĺžku 15 cm. Vypočítaj obsah trojuholníka a polomer vpísanej a opísanej kružnice.
Daný je rovnoramenný trojuholník, ktorého základňa je 8cm a ramená majú dĺžku 15 cm. Vypočítaj obsah trojuholníka a polomer vpísanej a opísanej kružnice. - Trojuholníku 83150
 V trojuholníku ABC poznáte pomer dĺžok strán a:b:c=3:4:6. Vypočítajte veľkosti uhlov trojuholníka ABC.
V trojuholníku ABC poznáte pomer dĺžok strán a:b:c=3:4:6. Vypočítajte veľkosti uhlov trojuholníka ABC. - Rovnostraný trojuholník
 Vypočítaj stranu rovnostraného trojuholníka, ak jeho obvod je 132 cm.
Vypočítaj stranu rovnostraného trojuholníka, ak jeho obvod je 132 cm. - Rebrík 15
 Rebrík dlhý 6,5 m je opretý o zvislú stenu. Jeho spodný koniec sa opiera o zem vo vzdialenosti 1,6 m od steny. Určte, do akej výšky dosahuje horný koniec rebríka a pod akým uhlom je rebrík opretý o stenu.
Rebrík dlhý 6,5 m je opretý o zvislú stenu. Jeho spodný koniec sa opiera o zem vo vzdialenosti 1,6 m od steny. Určte, do akej výšky dosahuje horný koniec rebríka a pod akým uhlom je rebrík opretý o stenu. - Deltoid 2
 Papierový šarkan má tvar deltoidu ABCD, v ktorom sú dve kratšie strany dlhé po 30 cm, dve dlhšie strany po 51 cm a kratšia uhlopriečka má dĺžku 48 cm. Určte veľkosti vnútorných uhlov daného deltoidu.
Papierový šarkan má tvar deltoidu ABCD, v ktorom sú dve kratšie strany dlhé po 30 cm, dve dlhšie strany po 51 cm a kratšia uhlopriečka má dĺžku 48 cm. Určte veľkosti vnútorných uhlov daného deltoidu. - Stúpanie cesty
 Na dopravnej značke, ktorá informuje o stúpaní cesty, je údaj 6,7 %. Určte uhol stúpania cesty. Aký výškový rozdiel prekonalo auto, ktoré prešlo po tejto ceste 2,8 km?
Na dopravnej značke, ktorá informuje o stúpaní cesty, je údaj 6,7 %. Určte uhol stúpania cesty. Aký výškový rozdiel prekonalo auto, ktoré prešlo po tejto ceste 2,8 km? - Značky
 Dopravné značky majú tvar rovnostranných trojuholníkov s dĺžkou strany 900 mm. Koľko eur stojí pozinkovaný plech na výrobu 50 kusov takýchto značiek, ak na odpad počítame s prídavkom 15% materiálu? Cena 1 meter štvorcový plechu je 6,5 eura.
Dopravné značky majú tvar rovnostranných trojuholníkov s dĺžkou strany 900 mm. Koľko eur stojí pozinkovaný plech na výrobu 50 kusov takýchto značiek, ak na odpad počítame s prídavkom 15% materiálu? Cena 1 meter štvorcový plechu je 6,5 eura. - Mimobežky
 Je daný kváder ABCDEFGH. Vieme, že |AB| = 1 cm, |BC| = 2 cm, |AE| = 3 cm. Vypočítajte v stupňoch veľkosť uhla, ktorý zvierajú priamky BG a FH .
Je daný kváder ABCDEFGH. Vieme, že |AB| = 1 cm, |BC| = 2 cm, |AE| = 3 cm. Vypočítajte v stupňoch veľkosť uhla, ktorý zvierajú priamky BG a FH . - Výška
 Výška je nakreslená z vrcholu rovnoramenného trojuholníka, ktorý tvorí pravý uhol a dva zhodné trojuholníky. Výsledkom je, že výška rozdeľuje základňu na dva rovnaké segmenty. Dĺžka výšky je 18 palcov a dĺžka základne je 15 palcov. Nájdite obvod trojuholn
Výška je nakreslená z vrcholu rovnoramenného trojuholníka, ktorý tvorí pravý uhol a dva zhodné trojuholníky. Výsledkom je, že výška rozdeľuje základňu na dva rovnaké segmenty. Dĺžka výšky je 18 palcov a dĺžka základne je 15 palcov. Nájdite obvod trojuholn
