Súčet členov geometrickej
V GP je a1 = 7, q = 5. Stanovte podmienku pre n, aby sn≤217.
Správna odpoveď:
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Konečná GP
 Určte zvyšné veličiny v konečnej geometrickej postupnosti, ak je dané: a1=18, an=13122, sn=19674, n=?, q=?
Určte zvyšné veličiny v konečnej geometrickej postupnosti, ak je dané: a1=18, an=13122, sn=19674, n=?, q=? - Diferencia
 Vypočítajte diferenciu aritmetickej postupnosti d, ak pre súčet jej prvých 12 členov platí: Sn= 5106 a prvý člen je a1 = 13
Vypočítajte diferenciu aritmetickej postupnosti d, ak pre súčet jej prvých 12 členov platí: Sn= 5106 a prvý člen je a1 = 13 - Medzi 14
 Medzi korene rovnice 4x² - 17x + 4= 0 vložte tri čísla tak, aby tvorili s danými číslami GP
Medzi korene rovnice 4x² - 17x + 4= 0 vložte tri čísla tak, aby tvorili s danými číslami GP - Aritmetickej 7917
 V aritmetickej postupnosti je dané: Sn=222, n=12, a1=2. Určite d, a12.
V aritmetickej postupnosti je dané: Sn=222, n=12, a1=2. Určite d, a12.
- Dané sú 4
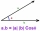 Dané sú vektory a = (3, -2), b = (-1, 5). Určte vektor c, pre ktorý platí a. c = 17, b. c = 3
Dané sú vektory a = (3, -2), b = (-1, 5). Určte vektor c, pre ktorý platí a. c = 17, b. c = 3 - Divné x
 Pre ktoré x platí x=17x?
Pre ktoré x platí x=17x? - Určte 7
 Určte zvyšné veličiny v konečnej geometrickej postupnosti, ak je dané: a1 = 5, an = 320, sn = 635, n=?, q=?
Určte zvyšné veličiny v konečnej geometrickej postupnosti, ak je dané: a1 = 5, an = 320, sn = 635, n=?, q=? - Kružnice
 Pre kružnice k1(S1; r1=192 cm) a k2(S2; r2 = 19 cm) platí že vzdialenosť stredov je |S1S2| = 234 cm. Určite vzdialenosť medzi kružnicami.
Pre kružnice k1(S1; r1=192 cm) a k2(S2; r2 = 19 cm) platí že vzdialenosť stredov je |S1S2| = 234 cm. Určite vzdialenosť medzi kružnicami. - Stredy tetív
 Kružnica s priemerom 17cm, hornou tetivou/CD/ = 10,2cm a dolnou tetivou/EF/ = 7,5cm, kde pre stredy tetív H, G platí /EH/ = 1/2 /EF/a /CG/ = 1/2 /CD/, určte vzdialenosť medzi bodom G a H. CD II EF.
Kružnica s priemerom 17cm, hornou tetivou/CD/ = 10,2cm a dolnou tetivou/EF/ = 7,5cm, kde pre stredy tetív H, G platí /EH/ = 1/2 /EF/a /CG/ = 1/2 /CD/, určte vzdialenosť medzi bodom G a H. CD II EF.
- Aritmetickej 61133
 Určte diferenciu aritmetickej postupnosti (an), ak je dané: a1=5, an=23, Sn=392
Určte diferenciu aritmetickej postupnosti (an), ak je dané: a1=5, an=23, Sn=392 - Určte 6
 Určte zvyšné veličiny v konečnej geometrickej postupnosti, ak je dané: n = 4, an = 12,5, sn = 187,5, a1=?, q=?
Určte zvyšné veličiny v konečnej geometrickej postupnosti, ak je dané: n = 4, an = 12,5, sn = 187,5, a1=?, q=? - Podivná GP
 Vypočítajte a3 GP, ak viete že q=4 a a1+a2+a3=89,25 a a4=272.
Vypočítajte a3 GP, ak viete že q=4 a a1+a2+a3=89,25 a a4=272. - GP - členy
 Aký je 5. člen geometrickej postupnosti, ak je 8. člen 80 a spoločný pomer (kvocient) r = 1/2?
Aký je 5. člen geometrickej postupnosti, ak je 8. člen 80 a spoločný pomer (kvocient) r = 1/2? - Na priamke
 Na priamke p: 3 x - 4 y - 3 = 0, stanovte súradnice bodu C, ktorý je rovnako vzdialený od bodov A [4, 4] a B [7, 1].
Na priamke p: 3 x - 4 y - 3 = 0, stanovte súradnice bodu C, ktorý je rovnako vzdialený od bodov A [4, 4] a B [7, 1].
- Dva kódy
 Pán O. si vymyslel dva kódy do trezoru, ktoré po týždni strieda. Oba kódy majú súčin číslic 120. V párny týždeň používa ako kód najmenšie možné číslo s touto vlastnosťou, v nepárny týždeň najväčšie. V žiadnom kóde nie je číslica 1, pretože tlačidlo s tout
Pán O. si vymyslel dva kódy do trezoru, ktoré po týždni strieda. Oba kódy majú súčin číslic 120. V párny týždeň používa ako kód najmenšie možné číslo s touto vlastnosťou, v nepárny týždeň najväčšie. V žiadnom kóde nie je číslica 1, pretože tlačidlo s tout - Pravdepodobnostnou 83202
 Finančný riaditeľ stanovil pre výnosnosť novej pobočky firmy nasledujúce scenáre ziskovosti: Zisk 5 mil Sk s pravdepodobnostnou 0,1. Zisk 3 mil Sk s pravdepodobnosťou 0,3. Zisk 1 mil Sk s pravdepodobnosťou 0,4. Strata 2 mil Sk s pravdepodobnosťou 0,2. Sta
Finančný riaditeľ stanovil pre výnosnosť novej pobočky firmy nasledujúce scenáre ziskovosti: Zisk 5 mil Sk s pravdepodobnostnou 0,1. Zisk 3 mil Sk s pravdepodobnosťou 0,3. Zisk 1 mil Sk s pravdepodobnosťou 0,4. Strata 2 mil Sk s pravdepodobnosťou 0,2. Sta - GP - jednoduché
 Urči piaty člen postupnosti, ak a1=-32, q=21
Urči piaty člen postupnosti, ak a1=-32, q=21
