Pre štatistický
Pre štatistický súbor:
2,3; 3,4; 1,8; 3,2; 3,2; 1,9; 3,3; 4,5; 4,3; 5,0; 4,8; 4,3; 4,3; 1,9
určte výberový rozptyl a medián, a z empirickej distribučnej funkcie určte P(2,1 < ξ < 3,5).
2,3; 3,4; 1,8; 3,2; 3,2; 1,9; 3,3; 4,5; 4,3; 5,0; 4,8; 4,3; 4,3; 1,9
určte výberový rozptyl a medián, a z empirickej distribučnej funkcie určte P(2,1 < ξ < 3,5).
Správna odpoveď:
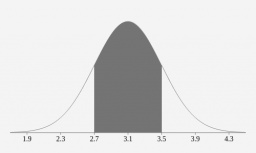
Zobrazujem 1 komentár:
Dr Math
Namiesto tabuliek sme pocitali cez : https://www.hackmath.net/sk/kalkulacka/normalne-rozdelenie
Tipy na súvisiace online kalkulačky
Hľadáte pomoc s výpočtom aritmetického priemeru?
Hľadáte štatistickú kalkulačku?
Hľadáte kalkulačku smerodajnej odchýlky?
Chceš si dať zrátať kombinačné číslo?
Hľadáte štatistickú kalkulačku?
Hľadáte kalkulačku smerodajnej odchýlky?
Chceš si dať zrátať kombinačné číslo?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Žiaci 22
 Žiaci maturitného ročníka na OA v Banskej Bystrici mali z písomky zo slovenského jazyka nasledujúce známky: 2, 2, 3, 3, 1, 4, 4, 2, 3, 5, 3, 3, 3, 4, 2, 4, 1, 1,2,3,4,5,1, 3, 3, 2, 2, 3, 2, 1. Vytvorte tabuľku rozdelenia početnosti, určte čo je štatistick
Žiaci maturitného ročníka na OA v Banskej Bystrici mali z písomky zo slovenského jazyka nasledujúce známky: 2, 2, 3, 3, 1, 4, 4, 2, 3, 5, 3, 3, 3, 4, 2, 4, 1, 1,2,3,4,5,1, 3, 3, 2, 2, 3, 2, 1. Vytvorte tabuľku rozdelenia početnosti, určte čo je štatistick - Smerodajná
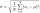 Vypočítajte smerodajnú odchýlku pre štatistický súbor dát: 63,65,68,69,69,72,75,76,77,79,79,80,82,83,84,88,90
Vypočítajte smerodajnú odchýlku pre štatistický súbor dát: 63,65,68,69,69,72,75,76,77,79,79,80,82,83,84,88,90 - Nespracovaných 39001
 Súbor údajov: 35 22 18 54 22 46 28 31 43 22 14 17 25 19 33 14. 1 Zoskupte údaje do zoskupeného rozdelenia pomocou 6 tried rovnakej šírky. 2. Určte priemer, medián a režim pomocou nespracovaných údajov. 3. Nakreslite krivku O-give zodpovedajúcu údajom a po
Súbor údajov: 35 22 18 54 22 46 28 31 43 22 14 17 25 19 33 14. 1 Zoskupte údaje do zoskupeného rozdelenia pomocou 6 tried rovnakej šírky. 2. Určte priemer, medián a režim pomocou nespracovaných údajov. 3. Nakreslite krivku O-give zodpovedajúcu údajom a po - Koeficient 82038
 Pre súbor údajov, ktorého koeficient šikmosti podľa Karla Pearsona = -2,25, rozptyl je 16 a priemer je 35, bude jeho stredná hodnota:
Pre súbor údajov, ktorého koeficient šikmosti podľa Karla Pearsona = -2,25, rozptyl je 16 a priemer je 35, bude jeho stredná hodnota: - Nezamestnanosť
 Za posledných 16 rokov sa miera nezamestnanosti krajiny menila podľa uvedenej frekvenčnej tabuľky: roky nezamestnanosti: 2 5 2 3 3 1 nezamestnanosť: 0,5 1 1,5 2 2,5 3 v % (percentách). Určte dvojstranný interval spoľahlivosti pre rozptyl DN s koeficientom
Za posledných 16 rokov sa miera nezamestnanosti krajiny menila podľa uvedenej frekvenčnej tabuľky: roky nezamestnanosti: 2 5 2 3 3 1 nezamestnanosť: 0,5 1 1,5 2 2,5 3 v % (percentách). Určte dvojstranný interval spoľahlivosti pre rozptyl DN s koeficientom - SD - priemer
 Priemer je 10 a štandardná odchýlka je 3,5. V prípade, že súbor dát obsahuje 40 hodnôt, približne, koľko hodnôt bude pohybovať v rozmedzí 6,5 až 13,5?
Priemer je 10 a štandardná odchýlka je 3,5. V prípade, že súbor dát obsahuje 40 hodnôt, približne, koľko hodnôt bude pohybovať v rozmedzí 6,5 až 13,5? - V našej
 V našej škole je v 5. ročníku 59 žiakov, v 6.ročníku 52, v siedmom je 86, v 8. ročníku 70 a v deviatom 71 žiakov. a) urči, čo je štatistický súbor. b) Urči, čo je štatistická jednotka. c) Urči čo je štatistický znak. d) Dané informácie zápíš do tabuľky. e
V našej škole je v 5. ročníku 59 žiakov, v 6.ročníku 52, v siedmom je 86, v 8. ročníku 70 a v deviatom 71 žiakov. a) urči, čo je štatistický súbor. b) Urči, čo je štatistická jednotka. c) Urči čo je štatistický znak. d) Dané informácie zápíš do tabuľky. e - V merani
 V merani 63 ziakov boli zistene nasledujuce udaje o vyske a prislusnom pocte ziakov: 159cm-1,161cm-1,162cm-2,163cm-1,164cm-2,165cm-2,166cm-3,167cm-2,168cm-4,169cm-3,170cm-5,171cm-6,172cm-7,173cm-9,174cm-5,175cm-2,177cm-1,178cm-4,179cm-2,181cm-1, a) urci a
V merani 63 ziakov boli zistene nasledujuce udaje o vyske a prislusnom pocte ziakov: 159cm-1,161cm-1,162cm-2,163cm-1,164cm-2,165cm-2,166cm-3,167cm-2,168cm-4,169cm-3,170cm-5,171cm-6,172cm-7,173cm-9,174cm-5,175cm-2,177cm-1,178cm-4,179cm-2,181cm-1, a) urci a - Špecializovaný 74654
 Špecializovaný učiteľ sleduje čas, ktorý každý zo študentov s poruchami učenia potrebuje na dokončenie psychologickej úlohy. Časy sumarizuje pomocou nasledovnej tabuľky: Čas (minúty) ; 1-5; 6-10; 11-12; 16-20 Počet študentov ; 2 ; 4 ; 12; 4 Pomocou uveden
Špecializovaný učiteľ sleduje čas, ktorý každý zo študentov s poruchami učenia potrebuje na dokončenie psychologickej úlohy. Časy sumarizuje pomocou nasledovnej tabuľky: Čas (minúty) ; 1-5; 6-10; 11-12; 16-20 Počet študentov ; 2 ; 4 ; 12; 4 Pomocou uveden - Určite 11
 Určite medián, modus, aritmetický priemer, rozptyl, smerodajnú odchýlku, variačné rozpätie a variačný koeficient znaku x v štatistickom súbore: 2x 9, 7x 10, 9x 11, 11x 15, 15x 17, 16x 19, 13x 21, 10x 25, 9x 29, 4x 32
Určite medián, modus, aritmetický priemer, rozptyl, smerodajnú odchýlku, variačné rozpätie a variačný koeficient znaku x v štatistickom súbore: 2x 9, 7x 10, 9x 11, 11x 15, 15x 17, 16x 19, 13x 21, 10x 25, 9x 29, 4x 32 - Pravdepodobnostnou 83202
 Finančný riaditeľ stanovil pre výnosnosť novej pobočky firmy nasledujúce scenáre ziskovosti: Zisk 5 mil Sk s pravdepodobnostnou 0,1. Zisk 3 mil Sk s pravdepodobnosťou 0,3. Zisk 1 mil Sk s pravdepodobnosťou 0,4. Strata 2 mil Sk s pravdepodobnosťou 0,2. Sta
Finančný riaditeľ stanovil pre výnosnosť novej pobočky firmy nasledujúce scenáre ziskovosti: Zisk 5 mil Sk s pravdepodobnostnou 0,1. Zisk 3 mil Sk s pravdepodobnosťou 0,3. Zisk 1 mil Sk s pravdepodobnosťou 0,4. Strata 2 mil Sk s pravdepodobnosťou 0,2. Sta - Máme 4,5
 Máme 4,5 litrov sirupu, a 80% tvori šťava. Koľko litrov bolo šťavy?
Máme 4,5 litrov sirupu, a 80% tvori šťava. Koľko litrov bolo šťavy? - Priemerná 20
 Priemerná výška príslušníka päťčlennej rodiny je 1,5m, modus ich výšok je 1,2m a medián 1,6m. Zistite, aké majú výšky jednotliví členovia tejto rodiny, ak viete, že sú to v dm celé čísla.
Priemerná výška príslušníka päťčlennej rodiny je 1,5m, modus ich výšok je 1,2m a medián 1,6m. Zistite, aké majú výšky jednotliví členovia tejto rodiny, ak viete, že sú to v dm celé čísla. - Štatistický 47843
 Nájdite 5-číselný štatistický súhrn týchto údajov a vytvorte si histogram (boxplot). 14,5,12,19,2,35,5,4,3,7,5,8
Nájdite 5-číselný štatistický súhrn týchto údajov a vytvorte si histogram (boxplot). 14,5,12,19,2,35,5,4,3,7,5,8 - Dané sú 4
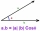 Dané sú vektory a = (3, -2), b = (-1, 5). Určte vektor c, pre ktorý platí a. c = 17, b. c = 3
Dané sú vektory a = (3, -2), b = (-1, 5). Určte vektor c, pre ktorý platí a. c = 17, b. c = 3 - Štatistický príklad
 Vypočítajte v súbore pacientov (priložená tabuľka 1) A) pomocou tabuľkového editora EXCEL B) programom „Social Science Statistics Calculator“ (SSSC) na web stránke a) priemerný vek pacientov a smerodajnú odchýlku (STDEV) b) priemernú dobu hospitalizácie a
Vypočítajte v súbore pacientov (priložená tabuľka 1) A) pomocou tabuľkového editora EXCEL B) programom „Social Science Statistics Calculator“ (SSSC) na web stránke a) priemerný vek pacientov a smerodajnú odchýlku (STDEV) b) priemernú dobu hospitalizácie a - Aritmetický 83270
 Známky s rovnakou váhou 2,1,3,2,2,3,1,3,1,1,2,4,2,2,3,1,1,2,1,3 urči: 1) aritmetický priemer 2) absolútna a relatívna frekvencia 3) modus a medián 4) vytvor graf
Známky s rovnakou váhou 2,1,3,2,2,3,1,3,1,1,2,4,2,2,3,1,1,2,1,3 urči: 1) aritmetický priemer 2) absolútna a relatívna frekvencia 3) modus a medián 4) vytvor graf
