Z7–I–4 2018 MO Betka
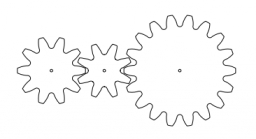
Betka sa hrala s ozubenými kolesami, ktoré ukladala tak, ako je naznačené na obrázku. Keď potom zatočila jedným okolo, točili sa všetky ostatné. Nakoniec bola spokojná so súkolesím, pričom prvé koleso malo 32 a druhé 24 zubov. Keď sa tretie koleso otočilo presne osemkrát, druhé koleso urobilo päť otáčok a časť šiestej a prvé koleso urobilo štyri otáčky a časť piatej.
Zistite, koľko zubov malo tretie koleso.
Zistite, koľko zubov malo tretie koleso.
Správna odpoveď:
Zobrazujem 1 komentár:
Dr Math
eseni zkusmo... Resp. na zacatku je rovnost:
8c = (5 a nieco) * b = (4 a nieco) * a
dosadzovanim prirodz. cisel za a,b,c dostanete raz spravni reseni...
8c = (5 a nieco) * b = (4 a nieco) * a
dosadzovanim prirodz. cisel za a,b,c dostanete raz spravni reseni...
Tipy na súvisiace online kalkulačky
Chceš si vypočítať najmenší spoločný násobok dvoch alebo viacerých čísel?
Riešite Diofantovské problémy a hľadáte kalkulačku diofantovských celočíselných rovníc?
Riešite Diofantovské problémy a hľadáte kalkulačku diofantovských celočíselných rovníc?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Ozubené kolesá
 Dve ozubené kolesá, ktoré do seba zapadajú majú počet zubov z1=109 a z2=165. Vypočítajte otáčky prvého kolesa, ak druhé koleso sa otáča 506 otáčok za minútu.
Dve ozubené kolesá, ktoré do seba zapadajú majú počet zubov z1=109 a z2=165. Vypočítajte otáčky prvého kolesa, ak druhé koleso sa otáča 506 otáčok za minútu. - Najmenšie 5394
 Ozubené súkolie je zostavené z troch ozubených kolies. Prvý má 165 zubov, druhý 132 zubov a tretí 231, pričom druhý zapadá do prvého a tretí do druhého kola. Prvý a tretí sa nedotýka. Koľkokrát za minútu budú všetky tri kolesá v rovnakom vzájomnom postave
Ozubené súkolie je zostavené z troch ozubených kolies. Prvý má 165 zubov, druhý 132 zubov a tretí 231, pričom druhý zapadá do prvého a tretí do druhého kola. Prvý a tretí sa nedotýka. Koľkokrát za minútu budú všetky tri kolesá v rovnakom vzájomnom postave - Čerpadlá 4
 V továrni použili na vyprázdnenie nádrže dve čerpadlá. Prvé čerpadlo nádrž vyprázdni za 50 minút, druhé za 30 min. Obidve čerpadlá spustili súčasne, no aby bola nádrž čo najskôr prázdna, po desiatich minútach spustili aj tretie čerpadlo. Všetky tri čerpad
V továrni použili na vyprázdnenie nádrže dve čerpadlá. Prvé čerpadlo nádrž vyprázdni za 50 minút, druhé za 30 min. Obidve čerpadlá spustili súčasne, no aby bola nádrž čo najskôr prázdna, po desiatich minútach spustili aj tretie čerpadlo. Všetky tri čerpad - Východiskovej 27121
 Dve ozubené kolesá – jedno menšie a jedno väčšie sa otáčajú tak, že zuby oboch kolies do seba zapadajú. Prvé kolo má 18 zubov, to druhé 27. Koľkokrát sa ktoré koleso otočí, než sa ocitnú opäť vo východiskovej polohe?
Dve ozubené kolesá – jedno menšie a jedno väčšie sa otáčajú tak, že zuby oboch kolies do seba zapadajú. Prvé kolo má 18 zubov, to druhé 27. Koľkokrát sa ktoré koleso otočí, než sa ocitnú opäť vo východiskovej polohe? - Existujú 7933
 Existujú tri spojené ozubené kolesá. Bicykel A má 30 zubov, bicykel B 15 zubov a bicykel C 20 zubov. Koľko otáčok vykoná koleso A, keď sa koleso C otočí 9 krát. a) 6, b) 5, c) 4 d) 8
Existujú tri spojené ozubené kolesá. Bicykel A má 30 zubov, bicykel B 15 zubov a bicykel C 20 zubov. Koľko otáčok vykoná koleso A, keď sa koleso C otočí 9 krát. a) 6, b) 5, c) 4 d) 8 - Velocipéd
 Predné koleso na velocipéde z r. 1880 malo priemer 1,8 m. Ak sa predné koleso otočilo raz a zadné 6-krát, potom aký bol priemer zadného kolesa?
Predné koleso na velocipéde z r. 1880 malo priemer 1,8 m. Ak sa predné koleso otočilo raz a zadné 6-krát, potom aký bol priemer zadného kolesa? - Predného 3991
 Obvod predného kolesa vozidla je 1,44 m, obvod zadného kolesa je 2,56 m. Ako dlho dráhu vozidlo prešlo, keď predné koleso urobilo o 560 otáčok viac ako zadné. Za neznámu voľte počet otáčok zadného kolesa.
Obvod predného kolesa vozidla je 1,44 m, obvod zadného kolesa je 2,56 m. Ako dlho dráhu vozidlo prešlo, keď predné koleso urobilo o 560 otáčok viac ako zadné. Za neznámu voľte počet otáčok zadného kolesa. - Súčin 16
 Súčin troch čísel je 224. Prvé z nich je 10, druhé je 50-krát menšie ako prvé. Vypočítajte tretie číslo.
Súčin troch čísel je 224. Prvé z nich je 10, druhé je 50-krát menšie ako prvé. Vypočítajte tretie číslo. - Tri čísla
 Nájdi tri čísla tak, aby druhé číslo bolo 4 krát väčší ako prvé a tretie bolo o 5 menšie ako druhe číslo. Ich súčet je 67.
Nájdi tri čísla tak, aby druhé číslo bolo 4 krát väčší ako prvé a tretie bolo o 5 menšie ako druhe číslo. Ich súčet je 67. - Tehly 3
 Na stavbu vozili tehly v troch nákladných autách. Jedno odviezlo naraz n tehál, druhé o m tehál menej ako prvé a na tretie sa zmestilo o 300 tehál viac ako na prvé auto. Prvé auto išlo 4-krát denne, najväčšie auto išlo 3-krát denne a najmenšie 5-krát denn
Na stavbu vozili tehly v troch nákladných autách. Jedno odviezlo naraz n tehál, druhé o m tehál menej ako prvé a na tretie sa zmestilo o 300 tehál viac ako na prvé auto. Prvé auto išlo 4-krát denne, najväčšie auto išlo 3-krát denne a najmenšie 5-krát denn - Súčin 3 čísel
 Súčin 3 čísel je 42. Prvé je 1,5 krát väčšie ako druhé číslo a tretie je 3,5 krát väčšie ako druhé číslo. O ktoré čísla ide?
Súčin 3 čísel je 42. Prvé je 1,5 krát väčšie ako druhé číslo a tretie je 3,5 krát väčšie ako druhé číslo. O ktoré čísla ide? - V elektrickom 2
 V elektrickom mixeri bol ozubený prevod. Hnacie koleso malo 24 zubov, hnané koleso malo 36 zubov. Kedy sa znovu stretli tie iste zuby oboch kolies?
V elektrickom mixeri bol ozubený prevod. Hnacie koleso malo 24 zubov, hnané koleso malo 36 zubov. Kedy sa znovu stretli tie iste zuby oboch kolies? - Dvojciferných 8012
 O koľko sa zmení súčet troch dvojciferných čísel keď prvé zväčšíme o 20, druhé zmenšíme o 10 a tretie ponecháme bez zmeny.
O koľko sa zmení súčet troch dvojciferných čísel keď prvé zväčšíme o 20, druhé zmenšíme o 10 a tretie ponecháme bez zmeny. - Materiál 23301
 Materiál, ktorého hmotnosť bola 18,2 t, odvážala tri autá. Druhé viezlo o 20% viac ako prvé a tretie 20% viac ako druhé. Koľko ton viezol každé?
Materiál, ktorého hmotnosť bola 18,2 t, odvážala tri autá. Druhé viezlo o 20% viac ako prvé a tretie 20% viac ako druhé. Koľko ton viezol každé? - Väčšie 3032
 Nájdi tri čísla tak, aby druhé číslo bolo 3krát väčšie ako prvé a tretie bolo o 6 väčšie ako druhé číslo. Ich súčet je 62
Nájdi tri čísla tak, aby druhé číslo bolo 3krát väčšie ako prvé a tretie bolo o 6 väčšie ako druhé číslo. Ich súčet je 62 - Bicykel
 Na bicykli má pedálove ozubené koleso 36 zubov, druhé prevodové koliesko má 10 zubov. Koľkokrát sa otočí prevodové koliesko, ak pedálove koleso sa otočí 120x?
Na bicykli má pedálove ozubené koleso 36 zubov, druhé prevodové koliesko má 10 zubov. Koľkokrát sa otočí prevodové koliesko, ak pedálove koleso sa otočí 120x? - Venček
 Na venček prišlo 12 chlapcov a 15 dievčat. Koľkými spôsobmi môžeme vybrať 4 tanečné páry?
Na venček prišlo 12 chlapcov a 15 dievčat. Koľkými spôsobmi môžeme vybrať 4 tanečné páry?
