Z6-I-6 MO 2018
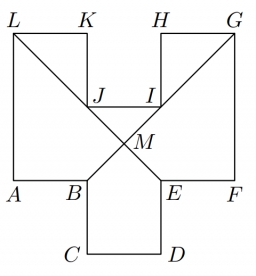
V dvanásťuholníku ABCDEFGHIJKL sú každé dve susedné strany navzájom kolmé a všetky strany s výnimkou strán AL a GF sú navzájom zhodné. Strany AL a GF sú oproti ostatným stranám dvojnásobne dlhé. Úsečky BG a EL sa pretínajú v bode M a rozdeľujú dvanásťuholník na šesť útvarov (tri trojuholníky, dva štvoruholníky a jeden päťuholník). Štvoruholník EFGM má obsah 7 cm2.
Určte obsahy ostatných piatich útvarov.
Určte obsahy ostatných piatich útvarov.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Potrebujete pomôcť spočítať, vykrátiť či vynásobiť zlomky? Skúste našu zlomkovú kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Z7–I–2 MO 2018
 V dvanásťuholníku ABCDEFGHIJKL sú každé dve susedné strany navzájom kolmé a všetky strany s výnimkou strán AL a GF sú navzájom zhodné. Strany AL a GF sú oproti ostatným stranám dvojnásobne dlhé. Úsečky BG a EL sa pretínajú v bode M. Štvoruholník ABMJ má o
V dvanásťuholníku ABCDEFGHIJKL sú každé dve susedné strany navzájom kolmé a všetky strany s výnimkou strán AL a GF sú navzájom zhodné. Strany AL a GF sú oproti ostatným stranám dvojnásobne dlhé. Úsečky BG a EL sa pretínajú v bode M. Štvoruholník ABMJ má o - Z8–I–5 MO 2019
 Pre osem navzájom rôznych bodov ako na obrázku platí, že body C, D, E ležia na priamke rovnobežnej s priamkou AB, F je stredom úsečky AD, G je stredom úsečky AC a H je priesečníkom priamok AC a BE. Obsah trojuholníka BCG je 12 cm² a obsah štvoruholníka DF
Pre osem navzájom rôznych bodov ako na obrázku platí, že body C, D, E ležia na priamke rovnobežnej s priamkou AB, F je stredom úsečky AD, G je stredom úsečky AC a H je priesečníkom priamok AC a BE. Obsah trojuholníka BCG je 12 cm² a obsah štvoruholníka DF - Trojuholník ABC
 V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC.
V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC. - Je daná
 Je daná kružnica k(S;2,5cm) a bod L ak |SL|=4cm. Zostrojte dotyčnicu ku kružnici, ktorá prechádza bodom L.
Je daná kružnica k(S;2,5cm) a bod L ak |SL|=4cm. Zostrojte dotyčnicu ku kružnici, ktorá prechádza bodom L.
- KLMN
 V lichobežníku KLMN platí že, strany KL a MN sú rovnobežné, úsečky KL a KM sú zhodné, úsečky KN, NM a ML sú navzájom zhodné. Určte veľkosť uhla KMN.
V lichobežníku KLMN platí že, strany KL a MN sú rovnobežné, úsečky KL a KM sú zhodné, úsečky KN, NM a ML sú navzájom zhodné. Určte veľkosť uhla KMN. - Obsah
 Vypočítajte obsah štvoruholníka, ktorého dve a dve strany sú rovnako dlhé a rovnobežné o dĺžkach strán 11, 5, 11 a 5. Vnútorné uhly štvoruholníka sú 45°, 135°,45°, 135°.
Vypočítajte obsah štvoruholníka, ktorého dve a dve strany sú rovnako dlhé a rovnobežné o dĺžkach strán 11, 5, 11 a 5. Vnútorné uhly štvoruholníka sú 45°, 135°,45°, 135°. - V rovnobežníku
 V rovnobežníku je dané: a, b-susedne strany, va, vb - príslušné výšky k jednotlivým stranám. Vypočítaj jeho stranu a, ak b=6cm, va=3cm, vb=4cm
V rovnobežníku je dané: a, b-susedne strany, va, vb - príslušné výšky k jednotlivým stranám. Vypočítaj jeho stranu a, ak b=6cm, va=3cm, vb=4cm - P trojúholníky
 Dĺžky odpovedajúcich si strán dvoch pravouhlých trojuholníkov sú v pomere 2:5. V akom pomere sú ťažnice príslušné na preponám týchto pravouhlých trojuholníkov a v akom pomere sú obsahy týchto trojuholníkov? Menší pravouhlý trojuholník má odvesny 6 cm a 8
Dĺžky odpovedajúcich si strán dvoch pravouhlých trojuholníkov sú v pomere 2:5. V akom pomere sú ťažnice príslušné na preponám týchto pravouhlých trojuholníkov a v akom pomere sú obsahy týchto trojuholníkov? Menší pravouhlý trojuholník má odvesny 6 cm a 8 - KOMPARO
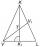 Na obrázku je rovnoramenný trojuholník VLK s ťažiskom T. Základňa VL meria 16 cm, ťažnica KK1 meria 18 cm. Akú dĺžku má ťažnica VV1?
Na obrázku je rovnoramenný trojuholník VLK s ťažiskom T. Základňa VL meria 16 cm, ťažnica KK1 meria 18 cm. Akú dĺžku má ťažnica VV1?
- Z5 – I – 2 MO 2018
 Tereza dostala štyri zhodné pravouhlé trojuholníky so stranami dĺžok 3 cm, 4 cm a 5 cm. Z týchto trojuholníkov (nie nutne zo všetkých štyroch) skúšala skladať nové útvary. Postupne sa jej podarilo zložiť štvoruholníky s obvodom 14 cm, 18 cm, 22 cm a 26 cm
Tereza dostala štyri zhodné pravouhlé trojuholníky so stranami dĺžok 3 cm, 4 cm a 5 cm. Z týchto trojuholníkov (nie nutne zo všetkých štyroch) skúšala skladať nové útvary. Postupne sa jej podarilo zložiť štvoruholníky s obvodom 14 cm, 18 cm, 22 cm a 26 cm - Deltoid 2
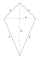 Papierový šarkan má tvar deltoidu ABCD, v ktorom sú dve kratšie strany dlhé po 30 cm, dve dlhšie strany po 51 cm a kratšia uhlopriečka má dĺžku 48 cm. Určte veľkosti vnútorných uhlov daného deltoidu.
Papierový šarkan má tvar deltoidu ABCD, v ktorom sú dve kratšie strany dlhé po 30 cm, dve dlhšie strany po 51 cm a kratšia uhlopriečka má dĺžku 48 cm. Určte veľkosti vnútorných uhlov daného deltoidu. - Lichobežník
 Sú uhlopriečky v pravouhlom lichobežníku navzájom kolmé a polia uhly?
Sú uhlopriečky v pravouhlom lichobežníku navzájom kolmé a polia uhly? - 4-uholník
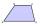 Je pravda že štvoruholník, ktorého dve strany sú rovnobežné a ďaľšie dve sú rovnako dlhé, je rovnobežník?
Je pravda že štvoruholník, ktorého dve strany sú rovnobežné a ďaľšie dve sú rovnako dlhé, je rovnobežník? - MO-Z6-I-2 2017
 Erika chcela ponúknuť čokoládu svojim trom kamarátkam. Keď ju vytiahla z batohu, zistila, že je polámaná ako na obrázku. (Vyznačené štvorčeky sú navzájom zhodné. ) Dievčatá sa dohodli, že čokoládu ďalej lámať nebudú a lósom určia, aký veľký kúsok ktorá do
Erika chcela ponúknuť čokoládu svojim trom kamarátkam. Keď ju vytiahla z batohu, zistila, že je polámaná ako na obrázku. (Vyznačené štvorčeky sú navzájom zhodné. ) Dievčatá sa dohodli, že čokoládu ďalej lámať nebudú a lósom určia, aký veľký kúsok ktorá do
- Skúste zostrojiť
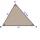 Skúste zostrojiť trojuholník MNP p=6cm , n=5cm, Vp=4cm Odpoveď zapíšte zmeranú dĺžku strany m
Skúste zostrojiť trojuholník MNP p=6cm , n=5cm, Vp=4cm Odpoveď zapíšte zmeranú dĺžku strany m - Dané sú 2
 Dané sú trojuholníky KLM a ABC, ktoré sú navzájom podobné. Dopočítaj dĺžky zvyšných strán trojuholníka KLM, ka dĺžky trán sú a=7 b=5,6 c=4,9 k=5
Dané sú trojuholníky KLM a ABC, ktoré sú navzájom podobné. Dopočítaj dĺžky zvyšných strán trojuholníka KLM, ka dĺžky trán sú a=7 b=5,6 c=4,9 k=5 - Osemsten
 Všetky steny pravidelného osemstena sú zhodne rovnostranne trojuholníky. Hrany osemstena ABCDEF majú dĺžku d=6 cm. Vypočítajte povrch a objem tohto osemstena.
Všetky steny pravidelného osemstena sú zhodne rovnostranne trojuholníky. Hrany osemstena ABCDEF majú dĺžku d=6 cm. Vypočítajte povrch a objem tohto osemstena.
