Asymptota
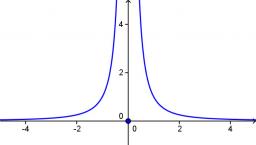
Určitě vertikální asymptotu funkce f(x)=2x+26−2x−8.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Funkce parabolická
 Je dána funkce y = x² - 4x + 3 Určete všechna reálná čísla z tak, aby platilo g(x) = g(-2).
Je dána funkce y = x² - 4x + 3 Určete všechna reálná čísla z tak, aby platilo g(x) = g(-2). - Výraz
 Určite hodnotu výrazu pre a = -1, b =2: x=b - 2a - ab y=a³ - b² - 2ab z=a² b³ - a³ b² w=a + b + a³ - b²
Určite hodnotu výrazu pre a = -1, b =2: x=b - 2a - ab y=a³ - b² - 2ab z=a² b³ - a³ b² w=a + b + a³ - b² - Hodnotu 3143
 Určite hodnotu výrazu 3x /2 - 5/2 - 0,5x + 1 pre x : a) x = 3 b) x = -3 c) x = 0
Určite hodnotu výrazu 3x /2 - 5/2 - 0,5x + 1 pre x : a) x = 3 b) x = -3 c) x = 0 - Premenných 3140
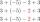 Určite hodnotu výrazu 3a + 2b - a² - 4b² pre hodnoty premenných : a) a = - 1, b = 3 b) a = 2, b = -1 c) a = -2, b = -3 d) a = 4, b = 2 e) a = -5, b = 0
Určite hodnotu výrazu 3a + 2b - a² - 4b² pre hodnoty premenných : a) a = - 1, b = 3 b) a = 2, b = -1 c) a = -2, b = -3 d) a = 4, b = 2 e) a = -5, b = 0
- Určite 69364
 Určite uhol ϕ: ϕ + 71°15' = 90°
Určite uhol ϕ: ϕ + 71°15' = 90° - Hodnoty 6621
 1) Je daná funkcia f: y = I 2-x I + 2 . Určite hodnoty funkcie v bodoch, tj F (-2), f(0), f (1), f (4,8).
1) Je daná funkcia f: y = I 2-x I + 2 . Určite hodnoty funkcie v bodoch, tj F (-2), f(0), f (1), f (4,8). - Sčítať a odčítať
 Určite hodnotu výrazu s desatinnými číslami: (4,416356)-7,152+(74,855)=?
Určite hodnotu výrazu s desatinnými číslami: (4,416356)-7,152+(74,855)=? - Vektory
 Pre vektor w platí: w = 4u+5v. Určite súradnice vektoru w, ak u=(6, 13), v=(12, 0)
Pre vektor w platí: w = 4u+5v. Určite súradnice vektoru w, ak u=(6, 13), v=(12, 0) - Diskriminant
 Určite diskriminant rovnice: x²-4x+59=1
Určite diskriminant rovnice: x²-4x+59=1
- Súradnice 59763
 Sú dané vektory v=(2,7; -1,8), w=(-3;2,5). Určite súradnice vektorov: a=v+w, b=v-w, c=w-v, d=2/3v
Sú dané vektory v=(2,7; -1,8), w=(-3;2,5). Určite súradnice vektorov: a=v+w, b=v-w, c=w-v, d=2/3v - C/y=x^2/(x^2-9) 4845
 Určite definičné odbory funkcií: a/y=2x-1 b/y=5x/(2x+1) c/y=x²/(x²-9)
Určite definičné odbory funkcií: a/y=2x-1 b/y=5x/(2x+1) c/y=x²/(x²-9) - Koeficient 21623
 V rovnici 2x² + bx-9=0 je jeden koreň x1=-3/2. Určite druhý koreň a koeficient b
V rovnici 2x² + bx-9=0 je jeden koreň x1=-3/2. Určite druhý koreň a koeficient b - Q:4x+7y-11=0 6374
 Určite priesečník dvoch priamok p a q ak je. : p:3y+2x-5=0 q:4x+7y-11=0
Určite priesečník dvoch priamok p a q ak je. : p:3y+2x-5=0 q:4x+7y-11=0 - Kvadratická rovnica
 Určite čísla b, c tak aby čísla x1 = -5 a x2 = -10 boli koreňmi kvadratickej rovnice: 4x ² + b x + c = 0
Určite čísla b, c tak aby čísla x1 = -5 a x2 = -10 boli koreňmi kvadratickej rovnice: 4x ² + b x + c = 0
