Hranol + Pytagorova veta - príklady a úlohy
Počet nájdených príkladov: 95
- Matematika 2
 Do prepravného kontajnera s rozmermi a=10 m, b=4m, c=3m bola umiestnená drevená debna s rozmermi d=3m, e=4m a f=3m. Aká je maximálna dĺžka rovnej neohybnej tyče so zanedbateľným priemerom, ktorú je možné v tejto situácii ešte do kontejnera umiestniť?
Do prepravného kontajnera s rozmermi a=10 m, b=4m, c=3m bola umiestnená drevená debna s rozmermi d=3m, e=4m a f=3m. Aká je maximálna dĺžka rovnej neohybnej tyče so zanedbateľným priemerom, ktorú je možné v tejto situácii ešte do kontejnera umiestniť? - Škatuľa 3
 Škatuľa má rozmery 30 cm, 40 cm, a 120 cm . Vojde do nej palička dlhá 128 cm?
Škatuľa má rozmery 30 cm, 40 cm, a 120 cm . Vojde do nej palička dlhá 128 cm? - Šperkovnica
 Šperkovnica je tvaru štvorbokého hranola s podstavou rovnoramenného lichobežníka so stranami a sa rovná 15 centimetrov b sa rovná 9 centimetrov c sa rovná 10 centimetrov v sa rovná 7 celá 4 centimetra. Koľko látky treba na obtiahnutie šperkovnice ak jej v
Šperkovnica je tvaru štvorbokého hranola s podstavou rovnoramenného lichobežníka so stranami a sa rovná 15 centimetrov b sa rovná 9 centimetrov c sa rovná 10 centimetrov v sa rovná 7 celá 4 centimetra. Koľko látky treba na obtiahnutie šperkovnice ak jej v - Rovnoramenného 24161
 Vypočítajte objem štvorbokého hranola, ktorý má podstavu rovnoramenného lichobežníka so základňami 10 cm a 4 cm, vzdialených od seba 6 cm . Výška hranola je 25 cm. Môžeš sa zamyslieť, ako by bolo možné vypočítať povrch?
Vypočítajte objem štvorbokého hranola, ktorý má podstavu rovnoramenného lichobežníka so základňami 10 cm a 4 cm, vzdialených od seba 6 cm . Výška hranola je 25 cm. Môžeš sa zamyslieť, ako by bolo možné vypočítať povrch?
- Obdĺžnikové 47863
 Nádrž má tvar kvádra. Dno je obdĺžnikové, jedna strana obdĺžnika má dĺžku 40cm, uhlopriečka tohto obdĺžnika je 50cm. Výška nádrže je 1,5m. Nádrž začíname plniť vodou rýchlosťou 1liter za sekundu. Žiadna voda neodteká. Vypočítaj, a) objem nádrže v litroch,
Nádrž má tvar kvádra. Dno je obdĺžnikové, jedna strana obdĺžnika má dĺžku 40cm, uhlopriečka tohto obdĺžnika je 50cm. Výška nádrže je 1,5m. Nádrž začíname plniť vodou rýchlosťou 1liter za sekundu. Žiadna voda neodteká. Vypočítaj, a) objem nádrže v litroch, - Vypočítajte 74
 Vypočítajte hmotnosť dreveného pravidelného trojbokého hranola s výškou rovnajúcou sa obvodu podstavy a postavou vpísanou do kružnice s polomerom 6, M cm, kde M je mesiac vášho narodenia. Hustota duba je 680 kg/m³.
Vypočítajte hmotnosť dreveného pravidelného trojbokého hranola s výškou rovnajúcou sa obvodu podstavy a postavou vpísanou do kružnice s polomerom 6, M cm, kde M je mesiac vášho narodenia. Hustota duba je 680 kg/m³. - Výška 18
 Výška pravidelného štvorbokého hranola je v=10 cm, odchýlka telesovej uhlopriečky od podstavy je 60°. Určte dĺžku podstavových hrán, povrch a objem kvádra.
Výška pravidelného štvorbokého hranola je v=10 cm, odchýlka telesovej uhlopriečky od podstavy je 60°. Určte dĺžku podstavových hrán, povrch a objem kvádra. - Trojboký 13
 Trojboký hranol má podstavu v tvare pravouhlého trojuholníka, ktorého odvesny majú dĺžku 9 cm a 40 cm. Výška hranola je 20 cm. Aký je jeho objem cm³? A povrch cm²?
Trojboký hranol má podstavu v tvare pravouhlého trojuholníka, ktorého odvesny majú dĺžku 9 cm a 40 cm. Výška hranola je 20 cm. Aký je jeho objem cm³? A povrch cm²? - Nádrž 20
 Nádrž má tvar pravidelného osembokého hranola bez hornej podstavy. Podstavná hrana má a= 3m, bočná hrana b=6m. Koľko plechu treba na zhotovenie nádrže? Neberte do úvahy straty, ani hrúbku plechu.
Nádrž má tvar pravidelného osembokého hranola bez hornej podstavy. Podstavná hrana má a= 3m, bočná hrana b=6m. Koľko plechu treba na zhotovenie nádrže? Neberte do úvahy straty, ani hrúbku plechu.
- Stĺp
 Vypočítajte objem a povrch podporného stĺpu tvare kolmého štvorbokého hranola, ktorého podstavou je kosoštvorec s uhlopriečku u1 = 102cm, u2 = 64cm. Výška stĺpa je 1,5m.
Vypočítajte objem a povrch podporného stĺpu tvare kolmého štvorbokého hranola, ktorého podstavou je kosoštvorec s uhlopriečku u1 = 102cm, u2 = 64cm. Výška stĺpa je 1,5m. - Podstava kosoštvorec
 Vypočítajte objem a povrch hranola, ktorého podstava je kosoštvorec s uhlopriečkami u1 = 13 cm, u2 = 18 cm. Výška hranola sa rovná dvojnásobku podstavovej hrany.
Vypočítajte objem a povrch hranola, ktorého podstava je kosoštvorec s uhlopriečkami u1 = 13 cm, u2 = 18 cm. Výška hranola sa rovná dvojnásobku podstavovej hrany. - Podstava
 Podstavu kolmého hranola tvorí pravouhlý trojuholník, ktorého odvesny majú pomer 3:4. Výška hranola je o 2cm menšia, ako väčšia odvesna. Určite objem hranola, ak jeho povrch je 468 cm².
Podstavu kolmého hranola tvorí pravouhlý trojuholník, ktorého odvesny majú pomer 3:4. Výška hranola je o 2cm menšia, ako väčšia odvesna. Určite objem hranola, ak jeho povrch je 468 cm². - Podstava 7
 Podstava kolmého trojbokého hranola je pravouhlý trojuholník, ktorého prepona je 10cm a jedna odvesna 8cm. Výška hranola je 75%z obvodu podstavy . Vypočítajte objem a povrch hranola.
Podstava kolmého trojbokého hranola je pravouhlý trojuholník, ktorého prepona je 10cm a jedna odvesna 8cm. Výška hranola je 75%z obvodu podstavy . Vypočítajte objem a povrch hranola. - Hranol 4b
 Vypočítajte objem a povrch pravidelného štvorbokého hranola ktorého výška je 28,6cm a telesová uhlopriečka zviera s rovinou podstavy uhol 50 stupňov.
Vypočítajte objem a povrch pravidelného štvorbokého hranola ktorého výška je 28,6cm a telesová uhlopriečka zviera s rovinou podstavy uhol 50 stupňov.
- Guľatina
 Priemer kmeňa je 85 cm. Je možné z neho vytesať hranol s podstavou štvorca o strane 62 cm?
Priemer kmeňa je 85 cm. Je možné z neho vytesať hranol s podstavou štvorca o strane 62 cm? - Litre vzduchu
 Vypočítajte, koľko litrov vzduchu sa zmestí do stanu, ktorý má štít tvaru rovnoramenného pravouhlého trojuholníka s ramenami r dlhými 3 m, výškou v = 1,5 m a dĺžkou d = 5 m.
Vypočítajte, koľko litrov vzduchu sa zmestí do stanu, ktorý má štít tvaru rovnoramenného pravouhlého trojuholníka s ramenami r dlhými 3 m, výškou v = 1,5 m a dĺžkou d = 5 m. - Ovnoramenného 3483
 Bazén tvaru kolmého hranola s dnom tvaru ovnoramenného lichobežníka rozmeroch základní lichobežníka 10m a 18m a ramenami 7m je hlboký 2m. Pri jarnom upratovaní treba vybieliť dno a steny bazéna. Koľko m² treba vybieliť?
Bazén tvaru kolmého hranola s dnom tvaru ovnoramenného lichobežníka rozmeroch základní lichobežníka 10m a 18m a ramenami 7m je hlboký 2m. Pri jarnom upratovaní treba vybieliť dno a steny bazéna. Koľko m² treba vybieliť? - Vzdialenosť 47493
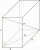 Je daný pravidelný štvorboký hranol ABCDEFGH s podstavnou hranou AB dĺžky 8 cm a výškou 6 cm. Bod M je stred hrany AE. Určite vzdialenosť bodu M od roviny BDH.
Je daný pravidelný štvorboký hranol ABCDEFGH s podstavnou hranou AB dĺžky 8 cm a výškou 6 cm. Bod M je stred hrany AE. Určite vzdialenosť bodu M od roviny BDH. - Trojboký hranol
 Rovina, ktorá prechádza hranou AB a stredom hrany CC´ pravidelného trojbokého hranola ABCA´B´C´ , zviera s podstavou uhol 39 stupňov, |AB| = 3 cm. Vypočítajte objem hranola.
Rovina, ktorá prechádza hranou AB a stredom hrany CC´ pravidelného trojbokého hranola ABCA´B´C´ , zviera s podstavou uhol 39 stupňov, |AB| = 3 cm. Vypočítajte objem hranola.
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
