Matematická olympiáda + sústava rovníc - príklady a úlohy
Počet nájdených príkladov: 36
- MO 2023
 V záhradkarskej osade mal pán Jahoda vo svojom sude 16.litrov vody. Sused Malina mal vo svojom sude tri krát viac vody, ako pán Jahoda. Začalo pršať a do oboch sudov napršalo rovnaké množstvo vody. Po daždi pán Malina zistil, že má v sude dvakrát viac vod
V záhradkarskej osade mal pán Jahoda vo svojom sude 16.litrov vody. Sused Malina mal vo svojom sude tri krát viac vody, ako pán Jahoda. Začalo pršať a do oboch sudov napršalo rovnaké množstvo vody. Po daždi pán Malina zistil, že má v sude dvakrát viac vod - MO Z7 2022
 Eva si myslela dve prirodzené čísla. Tieto najprv správne sčítala, potom správne odčítala. V obidvoch prípadoch dostala dvojciferný výsledok. Súčin takto vzniknutých dvojciferných čísel bol 645. Ktoré čísla si Eva myslela? Prosím vás aký je tento výsledok
Eva si myslela dve prirodzené čísla. Tieto najprv správne sčítala, potom správne odčítala. V obidvoch prípadoch dostala dvojciferný výsledok. Súčin takto vzniknutých dvojciferných čísel bol 645. Ktoré čísla si Eva myslela? Prosím vás aký je tento výsledok - Trojuholníkov 83111
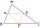 Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru
Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru - Skautskom MO 2023 z8
 V minulom roku bolo v našom skautskom oddiele o 30 chlapcov viac ako dievčat. Tento rok sa počet detí v oddiele zväčšil o 10%, pričom počet chlapcov sa zväčšil o 5% a počet dievčat sa zväčšil o 20%. Koľko detí máme tento rok v oddiele?
V minulom roku bolo v našom skautskom oddiele o 30 chlapcov viac ako dievčat. Tento rok sa počet detí v oddiele zväčšil o 10%, pričom počet chlapcov sa zväčšil o 5% a počet dievčat sa zväčšil o 20%. Koľko detí máme tento rok v oddiele?
- Odpočítajú 82333
 Myslím si tri čísla, keď ich sčítam dostanem 16, keď od súčtu prvých dvoch čísel odpočítajú tretie dostanem 10, keď od súčtu prvého a tretieho čísla odčítajú druhé dostanem 8. Ktoré čísla si myslím?
Myslím si tri čísla, keď ich sčítam dostanem 16, keď od súčtu prvých dvoch čísel odpočítajú tretie dostanem 10, keď od súčtu prvého a tretieho čísla odčítajú druhé dostanem 8. Ktoré čísla si myslím? - MO Z6-I-3 2022
 Magda si vystrihla dva rovnaké rovnoramenné trojuholníky, z ktorých každý mal obvod 100 cm. Najprv z týchto trojuholníkov zložila štvoruholník tak, že ich k sebe priložila ramenami. Potom z nich zložila štvoruholník tak, že ich k sebe priložila základňami
Magda si vystrihla dva rovnaké rovnoramenné trojuholníky, z ktorých každý mal obvod 100 cm. Najprv z týchto trojuholníkov zložila štvoruholník tak, že ich k sebe priložila ramenami. Potom z nich zložila štvoruholník tak, že ich k sebe priložila základňami - Floor zaokrúhľovanie nadol
 V obore reálnych čísel riešte sústavu rovníc: 2x + ⌊y⌋ = 2022, 3y + ⌊2x⌋ = 2023. (⌊a⌋ označuje (dolnú) celú časť reálneho čísla a, t. j. najväčšie celé číslo, ktoré nie je väčšie ako a. Napr. ⌊1,9⌋ = 1 a ⌊−1,1⌋ = −2.)
V obore reálnych čísel riešte sústavu rovníc: 2x + ⌊y⌋ = 2022, 3y + ⌊2x⌋ = 2023. (⌊a⌋ označuje (dolnú) celú časť reálneho čísla a, t. j. najväčšie celé číslo, ktoré nie je väčšie ako a. Napr. ⌊1,9⌋ = 1 a ⌊−1,1⌋ = −2.) - Polkrát 70014
 Matej a Anton sú starí dokopy 44 rokov. Matej je dvakrát taký starý, ako bol Anton v čase, keď bol Matej polkrát taký starý, ako bude Anton, až bude Anton 3x starší, než bol Matej, keď bol Matej 3x taký starý, ako Anton.
Matej a Anton sú starí dokopy 44 rokov. Matej je dvakrát taký starý, ako bol Anton v čase, keď bol Matej polkrát taký starý, ako bude Anton, až bude Anton 3x starší, než bol Matej, keď bol Matej 3x taký starý, ako Anton. - Trojnožky
 Na novo objavenej planéte žijú zvieratá, ktoré astronauti pomenovali podľa počtu nôh jednonožky, dvojnožky, trojnožky a tak ďalej (zvieratá bez nôh tam neboli). Zvieratá s nepárnym počtom nôh majú dve hlavy, zvieratá s párnym počtom nôh majú jednu hlavu.
Na novo objavenej planéte žijú zvieratá, ktoré astronauti pomenovali podľa počtu nôh jednonožky, dvojnožky, trojnožky a tak ďalej (zvieratá bez nôh tam neboli). Zvieratá s nepárnym počtom nôh majú dve hlavy, zvieratá s párnym počtom nôh majú jednu hlavu.
- MO Z7-II-1 2020
 Na rozprávkovom ostrove žijú draci a kyklopi. Všetci draci sú červení, trojhlaví a dvojnohí. Všetci kyklopi sú hnedí, jednohlaví a dvojnohí. Kyklopovia majú jedno oko uprostred čela, draci majú na každej hlave dve oči. Dohromady majú kyklopi a draci 42 oč
Na rozprávkovom ostrove žijú draci a kyklopi. Všetci draci sú červení, trojhlaví a dvojnohí. Všetci kyklopi sú hnedí, jednohlaví a dvojnohí. Kyklopovia majú jedno oko uprostred čela, draci majú na každej hlave dve oči. Dohromady majú kyklopi a draci 42 oč - Slávkine čísla
 Slávka si napísala farebnými fixkami štyri rôzne prirodzené čísla: červené, modré, zelené a žlté. Keď červené číslo vydelí modrým, dostane ako neúplný podiel zelené číslo a žlté predstavuje zvyšok po tomto delení. Keď vydelí modré číslo zeleným, vyjde jej
Slávka si napísala farebnými fixkami štyri rôzne prirodzené čísla: červené, modré, zelené a žlté. Keď červené číslo vydelí modrým, dostane ako neúplný podiel zelené číslo a žlté predstavuje zvyšok po tomto delení. Keď vydelí modré číslo zeleným, vyjde jej - MO 2019 Z8–I–4
 Pre päticu celých čísel platí, že keď k prvému pripočítame jednotku, druhé umocníme na druhú, od tretieho odčítame trojku, štvrté vynásobíme štyrmi a piate vydelíme piatimi, dostaneme zakaždým ten istý výsledok. Nájdite všetky také pätice čísel, ktorých s
Pre päticu celých čísel platí, že keď k prvému pripočítame jednotku, druhé umocníme na druhú, od tretieho odčítame trojku, štvrté vynásobíme štyrmi a piate vydelíme piatimi, dostaneme zakaždým ten istý výsledok. Nájdite všetky také pätice čísel, ktorých s - MO Z9-I-6 2019
 Kristína zvolila isté nepárne prirodzené číslo deliteľné tromi. Jakub s Dávidom potom skúmali trojuholníky, ktoré majú obvod v milimetroch rovný Kristínou zvolenému číslu a ktorých strany majú dĺžky v milimetroch vyjadrené navzájom rôznymi celými číslami.
Kristína zvolila isté nepárne prirodzené číslo deliteľné tromi. Jakub s Dávidom potom skúmali trojuholníky, ktoré majú obvod v milimetroch rovný Kristínou zvolenému číslu a ktorých strany majú dĺžky v milimetroch vyjadrené navzájom rôznymi celými číslami. - Z9 – I – 1 MO 2019
 Ondro, Maťo a Kubo sa vracajú zo zbierania orechov, dokopy ich majú 120. Maťo sa sťažuje, že Ondro má ako vždy najviac. Otec prikáže Ondrovi, aby prisypal zo svojho Maťovi tak, aby mu počet orechov zdvojnásobil. Teraz sa sťažuje Kubo, že najviac má Maťo.
Ondro, Maťo a Kubo sa vracajú zo zbierania orechov, dokopy ich majú 120. Maťo sa sťažuje, že Ondro má ako vždy najviac. Otec prikáže Ondrovi, aby prisypal zo svojho Maťovi tak, aby mu počet orechov zdvojnásobil. Teraz sa sťažuje Kubo, že najviac má Maťo.
- Matik - KSM
 V kuchárskej knihe od Mateja Matemakaka sa písalo: najväčší spoločný deliteľ gramáže múky a gramáže cukru je 15, najväčší spoločný deliteľ gramáže cukru a gramáže citrónovej kôry je 6, súčin gramáže cukru a gramáže citrónovej kôry je 1800, najmenší spoloč
V kuchárskej knihe od Mateja Matemakaka sa písalo: najväčší spoločný deliteľ gramáže múky a gramáže cukru je 15, najväčší spoločný deliteľ gramáže cukru a gramáže citrónovej kôry je 6, súčin gramáže cukru a gramáže citrónovej kôry je 1800, najmenší spoloč - Batožina lietadlom
 Dvaja priatelia cestujúci lietadlom mali dohromady 35 kg batožiny. Za nadváhu pri preprave zaplatil jeden 72 korún a druhý 108 korún. Keby za všetku batožinu platil len jeden, stálo by ho to 300 korún. Akú hmotnosť batožiny mal každý z nich, koľko kilogra
Dvaja priatelia cestujúci lietadlom mali dohromady 35 kg batožiny. Za nadváhu pri preprave zaplatil jeden 72 korún a druhý 108 korún. Keby za všetku batožinu platil len jeden, stálo by ho to 300 korún. Akú hmotnosť batožiny mal každý z nich, koľko kilogra - Samopočet
 Samopočet funguje presne ako kalkulačka. Hostinský chcel na samopočte sčítať niekoľko trojciferných prirodzených čísel. Na prvý pokus dostal výsledok 2224. Pre kontrolu sčítal tieto čísla znova a vyšlo mu 2198. Preto sčítal tieto čísla ešte raz a teraz do
Samopočet funguje presne ako kalkulačka. Hostinský chcel na samopočte sčítať niekoľko trojciferných prirodzených čísel. Na prvý pokus dostal výsledok 2224. Pre kontrolu sčítal tieto čísla znova a vyšlo mu 2198. Preto sčítal tieto čísla ešte raz a teraz do - Z7–I–5 MO 2018
 V záhradníctve Rose si jedna predajňa objednala celkom 120 ruží vo farbe červenej a žltej, druhá predajňa celkom 105 ruží vo farbe červenej a bielej a tretia predajňa celkom 45 ruží vo farbe žltej a bielej. Záhradníctvo zákazku splnilo, a to tak, že ruží
V záhradníctve Rose si jedna predajňa objednala celkom 120 ruží vo farbe červenej a žltej, druhá predajňa celkom 105 ruží vo farbe červenej a bielej a tretia predajňa celkom 45 ruží vo farbe žltej a bielej. Záhradníctvo zákazku splnilo, a to tak, že ruží - Z6-1-4 MO 2018
 Pán Ticháček mal na záhrade troch sadrových trpaslíkov: najväčšieho volal Maško, prostredného Jarko a najmenšieho Fanko. Keďže sa s nimi rád hrával, časom zistil, že keď postaví Fanka na Jarka, sú rovnako vysokí ako Maško. Keď naopak postaví Fanka na Mašk
Pán Ticháček mal na záhrade troch sadrových trpaslíkov: najväčšieho volal Maško, prostredného Jarko a najmenšieho Fanko. Keďže sa s nimi rád hrával, časom zistil, že keď postaví Fanka na Jarka, sú rovnako vysokí ako Maško. Keď naopak postaví Fanka na Mašk
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
