Mnohouholník + matematická olympiáda - príklady a úlohy
Počet nájdených príkladov: 10
- Trojuholník MO Z8-I-5
 Trojuholník ABC je rozdelený úsečkami. Úsečky DE a AB sú rovnobežné. Trojuholníky CDH, CHI, CIE, FIH majú rovnaký obsah a to 8 dm². Zistite obsah štvoruholníka AFHD.
Trojuholník ABC je rozdelený úsečkami. Úsečky DE a AB sú rovnobežné. Trojuholníky CDH, CHI, CIE, FIH majú rovnaký obsah a to 8 dm². Zistite obsah štvoruholníka AFHD. - Marienka - mo
 Marienka rozmiestni do vrcholov pravidelného osemuholníka rôzne počty od jedného po osem cukríkov. Peter si potom môže vybrať, ktoré tri kôpky cukríkov dá Marienke, ostatné si ponechá. Jedinou podmienkou je, že tieto tri kôpky ležia vo vrcholoch rovnorame
Marienka rozmiestni do vrcholov pravidelného osemuholníka rôzne počty od jedného po osem cukríkov. Peter si potom môže vybrať, ktoré tri kôpky cukríkov dá Marienke, ostatné si ponechá. Jedinou podmienkou je, že tieto tri kôpky ležia vo vrcholoch rovnorame - Päťuholník
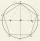 Vo vnútri pravidelného päťuholníka ABCDE je bod P taký, že trojuholník ABP je rovnostranný. Aký veľký je uhol BCP? Urob si náčrtok.
Vo vnútri pravidelného päťuholníka ABCDE je bod P taký, že trojuholník ABP je rovnostranný. Aký veľký je uhol BCP? Urob si náčrtok. - Osemsten súčet
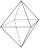 Na každej stene pravidelného osemstenu je napísané jedno z čísel 1, 2, 3, 4, 5, 6, 7 a 8, pričom na rôznych stenách sú rôzne čísla. Pri každej steny Janko určil súčet čísla na nej napísaného s číslami troch susedných stien. Takto dostal osem súčtov, ktoré
Na každej stene pravidelného osemstenu je napísané jedno z čísel 1, 2, 3, 4, 5, 6, 7 a 8, pričom na rôznych stenách sú rôzne čísla. Pri každej steny Janko určil súčet čísla na nej napísaného s číslami troch susedných stien. Takto dostal osem súčtov, ktoré - Šesťuholník nepravidelný
 Na obrázku je štvorec ABCD, štvorec EFGD a obdĺžnik HIJD. Body J a G ležia na strane CD, pričom platí |DJ| < |DG| a body H a E ležia na strane DA, pričom platí /DH/ < /DE/. Ďalej vieme, že/DJ/ = /GC/. Šesťuholník ABCGFE má obvod 96 cm, šesťuholník E
Na obrázku je štvorec ABCD, štvorec EFGD a obdĺžnik HIJD. Body J a G ležia na strane CD, pričom platí |DJ| < |DG| a body H a E ležia na strane DA, pričom platí /DH/ < /DE/. Ďalej vieme, že/DJ/ = /GC/. Šesťuholník ABCGFE má obvod 96 cm, šesťuholník E - Šesťuholníka 2340
 Je štvorec ABCD, štvorec EFGD a obdĺžnik HIJD, body JG ležia na strane CD pričom platí DJ je menší ako DG a body HE ležia na strane DA, pričom platí DH je menšia ako DE, ďalej vieme že DJ sa rovná GC. Šesťuholník ABCGFE má obvod 96 cm, šesťuholník EFGJIH
Je štvorec ABCD, štvorec EFGD a obdĺžnik HIJD, body JG ležia na strane CD pričom platí DJ je menší ako DG a body HE ležia na strane DA, pričom platí DH je menšia ako DE, ďalej vieme že DJ sa rovná GC. Šesťuholník ABCGFE má obvod 96 cm, šesťuholník EFGJIH - MO Z8–I–6 2018
 V lichobežníku KLMN má základňa KL veľkosť 40 cm a základňa MN má velkosť 16 cm. Bod P leží na úsečke KL tak, že úsečka NP rozdeľuje lichobežník na dve časti s rovnakými obsahmi. Určte veľkosť úsečky KP.
V lichobežníku KLMN má základňa KL veľkosť 40 cm a základňa MN má velkosť 16 cm. Bod P leží na úsečke KL tak, že úsečka NP rozdeľuje lichobežník na dve časti s rovnakými obsahmi. Určte veľkosť úsečky KP. - Z5 – I – 2 MO 2018
 Tereza dostala štyri zhodné pravouhlé trojuholníky so stranami dĺžok 3 cm, 4 cm a 5 cm. Z týchto trojuholníkov (nie nutne zo všetkých štyroch) skúšala skladať nové útvary. Postupne sa jej podarilo zložiť štvoruholníky s obvodom 14 cm, 18 cm, 22 cm a 26 cm
Tereza dostala štyri zhodné pravouhlé trojuholníky so stranami dĺžok 3 cm, 4 cm a 5 cm. Z týchto trojuholníkov (nie nutne zo všetkých štyroch) skúšala skladať nové útvary. Postupne sa jej podarilo zložiť štvoruholníky s obvodom 14 cm, 18 cm, 22 cm a 26 cm - Z6-I-6 MO 2018
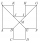 V dvanásťuholníku ABCDEFGHIJKL sú každé dve susedné strany navzájom kolmé a všetky strany s výnimkou strán AL a GF sú navzájom zhodné. Strany AL a GF sú oproti ostatným stranám dvojnásobne dlhé. Úsečky BG a EL sa pretínajú v bode M a rozdeľujú dvanásťuhol
V dvanásťuholníku ABCDEFGHIJKL sú každé dve susedné strany navzájom kolmé a všetky strany s výnimkou strán AL a GF sú navzájom zhodné. Strany AL a GF sú oproti ostatným stranám dvojnásobne dlhé. Úsečky BG a EL sa pretínajú v bode M a rozdeľujú dvanásťuhol - Z7–I–2 MO 2018
 V dvanásťuholníku ABCDEFGHIJKL sú každé dve susedné strany navzájom kolmé a všetky strany s výnimkou strán AL a GF sú navzájom zhodné. Strany AL a GF sú oproti ostatným stranám dvojnásobne dlhé. Úsečky BG a EL sa pretínajú v bode M. Štvoruholník ABMJ má o
V dvanásťuholníku ABCDEFGHIJKL sú každé dve susedné strany navzájom kolmé a všetky strany s výnimkou strán AL a GF sú navzájom zhodné. Strany AL a GF sú oproti ostatným stranám dvojnásobne dlhé. Úsečky BG a EL sa pretínajú v bode M. Štvoruholník ABMJ má o
Ospravedlňujeme sa, ale v tejto kategórií nie je veľa príkladov.
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
