Úvaha + matematická olympiáda - príklady a úlohy
Počet nájdených príkladov: 145
- Priklad – 8. rocnik (asi MO)
 Adam napı́sal nasledujúci súčet s piatimi tajnými sčı́tancami: a + bb + ccc + dddd + eeeee. Prezradil, že znaky „a, b, c, d, e“ predstavujú navzájom rôzne cifry 1, 2, 3, 4, 5 a že výsledný súčet je deliteľný 11. Ktoré najmenšie a ktoré na
Adam napı́sal nasledujúci súčet s piatimi tajnými sčı́tancami: a + bb + ccc + dddd + eeeee. Prezradil, že znaky „a, b, c, d, e“ predstavujú navzájom rôzne cifry 1, 2, 3, 4, 5 a že výsledný súčet je deliteľný 11. Ktoré najmenšie a ktoré na - Zajac 2024m
 Zajac sa zúčastnil na pretekoch dlhých 2024 metrov. Zo štartovej čiary sa odrazil ľavou nohou a po celý čas pretekov pravidelne striedal ľavú, pravú a obe nohy. Keď sa zajac odrazil ľavou nohou, skočil 35 dm, keď sa odrazil pravou nohou, skočil 15
Zajac sa zúčastnil na pretekoch dlhých 2024 metrov. Zo štartovej čiary sa odrazil ľavou nohou a po celý čas pretekov pravidelne striedal ľavú, pravú a obe nohy. Keď sa zajac odrazil ľavou nohou, skočil 35 dm, keď sa odrazil pravou nohou, skočil 15 - Karol 9
 Karol mal vynásobiť dve dvojciferné čísla. Z nepozornosti vymenil poradie cifier v jednom z činiteľov a dostal súčin, ktorý bol o 4 248 menší ako správny výsledok. Aký je správny výsledok? Koľko malo Karolovi správne vyjsť?
Karol mal vynásobiť dve dvojciferné čísla. Z nepozornosti vymenil poradie cifier v jednom z činiteľov a dostal súčin, ktorý bol o 4 248 menší ako správny výsledok. Aký je správny výsledok? Koľko malo Karolovi správne vyjsť? - Štvoruholník 14
 Daný je štvorec ABCD. Stred AB je E, stred BC je F, CD je G a stred DA je H. Spojíme AF, BG, CH a DE. Vo vnútri štvorca (približne v strede) priesečníky týchto úsečiek vytvoria štvoruholník. Vypočítajte obsah tohto štvoruholníka. Ďakujem
Daný je štvorec ABCD. Stred AB je E, stred BC je F, CD je G a stred DA je H. Spojíme AF, BG, CH a DE. Vo vnútri štvorca (približne v strede) priesečníky týchto úsečiek vytvoria štvoruholník. Vypočítajte obsah tohto štvoruholníka. Ďakujem - Nikola
 Nikola mala v zošite napísané jedno trojciferne a jedno dvojciferné číslo. Každé z týchto čísel bolo tvorené navzájom rôznymi číslicami. Rozdiel Nikolinych čísel bol 976. Aký bol ich súčet?
Nikola mala v zošite napísané jedno trojciferne a jedno dvojciferné číslo. Každé z týchto čísel bolo tvorené navzájom rôznymi číslicami. Rozdiel Nikolinych čísel bol 976. Aký bol ich súčet? - Trojuholníkov 83111
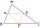 Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru
Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru - Skautskom MO 2023 z8
 V minulom roku bolo v našom skautskom oddiele o 30 chlapcov viac ako dievčat. Tento rok sa počet detí v oddiele zväčšil o 10%, pričom počet chlapcov sa zväčšil o 5% a počet dievčat sa zväčšil o 20%. Koľko detí máme tento rok v oddiele?
V minulom roku bolo v našom skautskom oddiele o 30 chlapcov viac ako dievčat. Tento rok sa počet detí v oddiele zväčšil o 10%, pričom počet chlapcov sa zväčšil o 5% a počet dievčat sa zväčšil o 20%. Koľko detí máme tento rok v oddiele? - MO 2022
 Petra mala napísané prirodzené čísla od 1 do 9. Dve z týchto čísel sčítala, zmazala a výsledný súčet napísala miesto sčítancov. Mala tak napísané osem čísel, ktoré sa jej podarilo rozdeliť do dvoch skupín s rovnakým súčinom. Určite aký najväčší mohol byť
Petra mala napísané prirodzené čísla od 1 do 9. Dve z týchto čísel sčítala, zmazala a výsledný súčet napísala miesto sčítancov. Mala tak napísané osem čísel, ktoré sa jej podarilo rozdeliť do dvoch skupín s rovnakým súčinom. Určite aký najväčší mohol byť - MO Z7 2022
 Priemerný vek starého otca, babičky a ich piatich vnúčat je 26 rokov. Priemerný vek samotných vnúčat je 7 rokov. Babička je o rok mladšia ako dedo. Koľko rokov je babičke?
Priemerný vek starého otca, babičky a ich piatich vnúčat je 26 rokov. Priemerný vek samotných vnúčat je 7 rokov. Babička je o rok mladšia ako dedo. Koľko rokov je babičke? - Najmenšie z9 2022
 Nájdite najmenšie kladné čísla a a b, pre ktoré platia 7a³ = 11b⁵
Nájdite najmenšie kladné čísla a a b, pre ktoré platia 7a³ = 11b⁵ - Splnenie 80562
 Koľko rôznych množín kladného celého čísla v tvare (x, y, z) na splnenie rovnice xyz=1400?
Koľko rôznych množín kladného celého čísla v tvare (x, y, z) na splnenie rovnice xyz=1400? - Aritmetickú 80551
 Bolek a Lolek mali každý svoju aritmetickú postupnosť. Ako Lolek, tak Bolek postupnosť začínala číslom 2023 a končila číslom 3023. Tieto dve postupnosti mali 26 spoločných čísel. Pomer Bolkovej a Lolkovej diferencie bol 5:2. Aký rozdiel Bolkovej a Lolkove
Bolek a Lolek mali každý svoju aritmetickú postupnosť. Ako Lolek, tak Bolek postupnosť začínala číslom 2023 a končila číslom 3023. Tieto dve postupnosti mali 26 spoločných čísel. Pomer Bolkovej a Lolkovej diferencie bol 5:2. Aký rozdiel Bolkovej a Lolkove - Floor zaokrúhľovanie nadol
 V obore reálnych čísel riešte sústavu rovníc: 2x + ⌊y⌋ = 2022, 3y + ⌊2x⌋ = 2023. (⌊a⌋ označuje (dolnú) celú časť reálneho čísla a, t. j. najväčšie celé číslo, ktoré nie je väčšie ako a. Napr. ⌊1,9⌋ = 1 a ⌊−1,1⌋ = −2.)
V obore reálnych čísel riešte sústavu rovníc: 2x + ⌊y⌋ = 2022, 3y + ⌊2x⌋ = 2023. (⌊a⌋ označuje (dolnú) celú časť reálneho čísla a, t. j. najväčšie celé číslo, ktoré nie je väčšie ako a. Napr. ⌊1,9⌋ = 1 a ⌊−1,1⌋ = −2.) - Polkrát 70014
 Matej a Anton sú starí dokopy 44 rokov. Matej je dvakrát taký starý, ako bol Anton v čase, keď bol Matej polkrát taký starý, ako bude Anton, až bude Anton 3x starší, než bol Matej, keď bol Matej 3x taký starý, ako Anton.
Matej a Anton sú starí dokopy 44 rokov. Matej je dvakrát taký starý, ako bol Anton v čase, keď bol Matej polkrát taký starý, ako bude Anton, až bude Anton 3x starší, než bol Matej, keď bol Matej 3x taký starý, ako Anton. - Dedecek 63074
 Môj jediný syn sa narodil keď som mal 37 rokov. to bolo práve 32 rokov po smrti dedka a ten zomrel vo svojich 64 rokoch. Dedecek bol o 12 rokov starší ako babička, brali sa v roku 1947 práve keď babičke bolo 18 rokov. V ktorom roku sa narodil môj syn?
Môj jediný syn sa narodil keď som mal 37 rokov. to bolo práve 32 rokov po smrti dedka a ten zomrel vo svojich 64 rokoch. Dedecek bol o 12 rokov starší ako babička, brali sa v roku 1947 práve keď babičke bolo 18 rokov. V ktorom roku sa narodil môj syn? - Nakupoval 61153
 Vodník Kebule nakupoval v rybárni kapitána Nema, kde ceny všetkého tovaru boli uvedené v celých šupinách. Keby Kebule kúpil 2 raky, 3 mušle, a 1 šťuku, zaplatil by 49 šupín. Ak by prikúpil ešte 5 rákov, 11 mušlí a 1 šťuku, platil by celkom 154 šupín. Koľk
Vodník Kebule nakupoval v rybárni kapitána Nema, kde ceny všetkého tovaru boli uvedené v celých šupinách. Keby Kebule kúpil 2 raky, 3 mušle, a 1 šťuku, zaplatil by 49 šupín. Ak by prikúpil ešte 5 rákov, 11 mušlí a 1 šťuku, platil by celkom 154 šupín. Koľk - Deti MO Z7 2021
 Súčin vekov všetkých detí pána Násobka je 1408. Vek najmladšieho dieťaťa je rovný polovici veku najstaršieho dieťaťa. Koľko detí má pán Násobok a koľko má rokov?
Súčin vekov všetkých detí pána Násobka je 1408. Vek najmladšieho dieťaťa je rovný polovici veku najstaršieho dieťaťa. Koľko detí má pán Násobok a koľko má rokov? - Trojnožky
 Na novo objavenej planéte žijú zvieratá, ktoré astronauti pomenovali podľa počtu nôh jednonožky, dvojnožky, trojnožky a tak ďalej (zvieratá bez nôh tam neboli). Zvieratá s nepárnym počtom nôh majú dve hlavy, zvieratá s párnym počtom nôh majú jednu hlavu.
Na novo objavenej planéte žijú zvieratá, ktoré astronauti pomenovali podľa počtu nôh jednonožky, dvojnožky, trojnožky a tak ďalej (zvieratá bez nôh tam neboli). Zvieratá s nepárnym počtom nôh majú dve hlavy, zvieratá s párnym počtom nôh majú jednu hlavu. - Určte
 Určte počet deväťmiestnych čı́sel, v ktorých sa každá z čı́slic 0 až 9 vyskytuje najviac raz a v ktorých sa súčty čı́slic na 1. až 3. mieste, na 3. až 5. mieste, na 5. až 7. mieste a na 7. až 9. mieste vždy rovnajú 10. Nájdite aj najme
Určte počet deväťmiestnych čı́sel, v ktorých sa každá z čı́slic 0 až 9 vyskytuje najviac raz a v ktorých sa súčty čı́slic na 1. až 3. mieste, na 3. až 5. mieste, na 5. až 7. mieste a na 7. až 9. mieste vždy rovnajú 10. Nájdite aj najme - Dva prístavy
 Medzi prístavy Mumraj a Zmätok pendlujú po rovnakej trase dve lode. V prístavoch trávia zanedbateľný čas, hneď sa otáčajú a pokračujú v plavbe. Ráno v rovnaký okamih vypláva modrá loď z prístavu Mumraj a zelená loď z prístavu Zmätok. Prvýkrát sa lode míňa
Medzi prístavy Mumraj a Zmätok pendlujú po rovnakej trase dve lode. V prístavoch trávia zanedbateľný čas, hneď sa otáčajú a pokračujú v plavbe. Ráno v rovnaký okamih vypláva modrá loď z prístavu Mumraj a zelená loď z prístavu Zmätok. Prvýkrát sa lode míňa
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
