Úvaha + matematická olympiáda - príklady a úlohy - strana 6 z 8
Počet nájdených príkladov: 145
- Štvormiestne 5312
 Nájdite najmenšie štvormiestne číslo abcd také, že rozdiel (ab)2−(cd)2 je trojmiestne číslo zapísané tromi rovnakými číslicami.
Nájdite najmenšie štvormiestne číslo abcd také, že rozdiel (ab)2−(cd)2 je trojmiestne číslo zapísané tromi rovnakými číslicami. - Starý hodinár
 Starý hodinár má vo svojej zbierke zvláštny digitálny budík, ktorý zvoní vždy, keď súčet cifier, ktorý budík ukazuje, sa rovná číslu 21. Zisti, v ktorých časoch bude budík zvoniť. Aký je ich počet? Vypíš všetky možnosti...
Starý hodinár má vo svojej zbierke zvláštny digitálny budík, ktorý zvoní vždy, keď súčet cifier, ktorý budík ukazuje, sa rovná číslu 21. Zisti, v ktorých časoch bude budík zvoniť. Aký je ich počet? Vypíš všetky možnosti... - Čokoláda 6
 Medzinárodná banda pašerákov čokolády vedená slávnym Jackom Krivým Nosom, ktorý má 7 spolupracovníkov, si vytipovalal bratislavské letisko ako križovatku svojich obchodov. Lietadlo z Bratislavy do Štokholmu lieta každý tretí deň. Lietadlo z Bratislavy do
Medzinárodná banda pašerákov čokolády vedená slávnym Jackom Krivým Nosom, ktorý má 7 spolupracovníkov, si vytipovalal bratislavské letisko ako križovatku svojich obchodov. Lietadlo z Bratislavy do Štokholmu lieta každý tretí deň. Lietadlo z Bratislavy do - Kyvadlová doprava
 Rieka dlhá 777 km preteká lesom i pasienkami a sem-tam sa na jej brehu mihne prístav. Medzi 2 z 5 prístavov na rieke je trvalá kyvadlová doprava. Zabezpečuje ju 77 rokov stará loď Quendolína s kapitánom Modrofúzom, ktorý má 100 rokov a ešte 15 zubov. Quen
Rieka dlhá 777 km preteká lesom i pasienkami a sem-tam sa na jej brehu mihne prístav. Medzi 2 z 5 prístavov na rieke je trvalá kyvadlová doprava. Zabezpečuje ju 77 rokov stará loď Quendolína s kapitánom Modrofúzom, ktorý má 100 rokov a ešte 15 zubov. Quen - Bicykle
 Si majiteľ dopravného ihriska. Kúp bicykle dvoch farieb ľubovoľného počtu, ale musíš minúť presne 120000Kč. Modrý bicykel stojí 3600Kč a červený bicykel stojí 3200Kč.
Si majiteľ dopravného ihriska. Kúp bicykle dvoch farieb ľubovoľného počtu, ale musíš minúť presne 120000Kč. Modrý bicykel stojí 3600Kč a červený bicykel stojí 3200Kč. - MO Z6-6-1
 Do prázdnych polí v nasledujúcom obrázku doplňte celé čísla väčšie ako 1 tak, aby v každom tmavšom políčku bol súčin čísel zo susedných svetlejších políčok: Aké je číslo je v strede?
Do prázdnych polí v nasledujúcom obrázku doplňte celé čísla väčšie ako 1 tak, aby v každom tmavšom políčku bol súčin čísel zo susedných svetlejších políčok: Aké je číslo je v strede? - Z7-I-4 hviezdičky 4949
 Napíšte namiesto hviezdičiek, aby nasledujúci zápis súčinu dvoch čísel bol platný: ∗ ∗ ∗ · ∗ ∗ ∗ ∗ ∗ ∗ ∗ 4 9 4 9 ∗ ∗ ∗ ∗ ∗ ∗ 4 ∗ ∗
Napíšte namiesto hviezdičiek, aby nasledujúci zápis súčinu dvoch čísel bol platný: ∗ ∗ ∗ · ∗ ∗ ∗ ∗ ∗ ∗ ∗ 4 9 4 9 ∗ ∗ ∗ ∗ ∗ ∗ 4 ∗ ∗ - Pyramída Z8–I–6
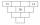 Každá tehlička zobrazenej pyramídy obsahuje jedno číslo. Kedykoľvek to je možné, je číslo v každej tehličke najmenším spoločným násobkom čísel z dvoch tehličiek ležiacich priamo nad ňou. Ktoré číslo môže byť v najspodnejšej tehličke? Určite všetky možnost
Každá tehlička zobrazenej pyramídy obsahuje jedno číslo. Kedykoľvek to je možné, je číslo v každej tehličke najmenším spoločným násobkom čísel z dvoch tehličiek ležiacich priamo nad ňou. Ktoré číslo môže byť v najspodnejšej tehličke? Určite všetky možnost - Celočíselnými 4445
 Nájdete všetky trojčleny P(x) = a * x² + b * x + c s celočíselnými koeficientmi a, b a c, pre ktoré platí P(1) < P(2) < P(3) a zároveň ((P(1)) ² + ((P(2)) ² + ((P(3)) ² = 22).
Nájdete všetky trojčleny P(x) = a * x² + b * x + c s celočíselnými koeficientmi a, b a c, pre ktoré platí P(1) < P(2) < P(3) a zároveň ((P(1)) ² + ((P(2)) ² + ((P(3)) ² = 22). - Stromčekov 4433
 Predavač vianočných stromčekov predával smrečky za 220 Sk, borovičky po 250 Sk a jedličky po 330 Sk. Ráno mal rovnaký počet smrekov, jedličiek a borovíc. Večer mal všetky stromčeky predané a celkom za ne utŕžil 36000 Sk. Koľko stromčekov predavač toho dňa
Predavač vianočných stromčekov predával smrečky za 220 Sk, borovičky po 250 Sk a jedličky po 330 Sk. Ráno mal rovnaký počet smrekov, jedličiek a borovíc. Večer mal všetky stromčeky predané a celkom za ne utŕžil 36000 Sk. Koľko stromčekov predavač toho dňa - MO-I-Z6
 Štvorec so stranou 4 cm je rozdelený na štvorčeky so stranou 1 cm ako na obrázku. Rozdeľte štvorec pozdĺž vyznačených čiar na dva útvary s obvodom 16 cm. Nájdite aspoň tri rôzne riešenia (tzn. také tri riešenia, aby žiadny útvar jedného riešenia nebol zho
Štvorec so stranou 4 cm je rozdelený na štvorčeky so stranou 1 cm ako na obrázku. Rozdeľte štvorec pozdĺž vyznačených čiar na dva útvary s obvodom 16 cm. Nájdite aspoň tri rôzne riešenia (tzn. také tri riešenia, aby žiadny útvar jedného riešenia nebol zho - Lichobežník MO-5-Z8
 Lichobežník ABCD je úsečkou CE rozdelený na trojuholník a rovnobežník, viď obrázok. Bod F je stredom úsečky CE, priamka DF prechádza stredom úsečky BE a obsah trojuholníka CDE je 3 cm². Určte obsah lichobežníka ABCD.
Lichobežník ABCD je úsečkou CE rozdelený na trojuholník a rovnobežník, viď obrázok. Bod F je stredom úsečky CE, priamka DF prechádza stredom úsečky BE a obsah trojuholníka CDE je 3 cm². Určte obsah lichobežníka ABCD. - Zákusky Z8-I-5
 Mamička doniesla 10 zákuskov troch druhov: kokosiek bolo menej ako laskonek a najviac bolo karamelových kociek. Jaro si vybral dva zákusky rôznych druhov, Štefan urobil to isté a na Marcelu ostali len zákusky rovnakého druhu. Koľko kokosiek, laskonek a ka
Mamička doniesla 10 zákuskov troch druhov: kokosiek bolo menej ako laskonek a najviac bolo karamelových kociek. Jaro si vybral dva zákusky rôznych druhov, Štefan urobil to isté a na Marcelu ostali len zákusky rovnakého druhu. Koľko kokosiek, laskonek a ka - Štyri rodiny MO-Z6-I-4
 Štyri rodiny boli na spoločnom výlete. V prvej rodine boli traja súrodenci, a to Alica, Betka a Cyril. V druhej rodine boli štyria súrodenci, a to Dávid, Erika, Filipa a Gabika. V tretej rodine boli dvaja súrodenci, a to Hugo a Iveta. Vo štvrtej rodine bo
Štyri rodiny boli na spoločnom výlete. V prvej rodine boli traja súrodenci, a to Alica, Betka a Cyril. V druhej rodine boli štyria súrodenci, a to Dávid, Erika, Filipa a Gabika. V tretej rodine boli dvaja súrodenci, a to Hugo a Iveta. Vo štvrtej rodine bo - Hviezdičky - MO - Z5 - 66
 Napíšte namiesto hviezdičiek cifry tak, aby súčet doplnených cifier bol nepárny a aby platila uvedená rovnosť: 42 · ∗8 = 2 ∗∗∗
Napíšte namiesto hviezdičiek cifry tak, aby súčet doplnených cifier bol nepárny a aby platila uvedená rovnosť: 42 · ∗8 = 2 ∗∗∗ - Stonožka
 Stonožka Mirka pozostáva z hlavy a niekoľkých článkov, na každom článku má jeden pár nôh. Keď sa ochladilo, rozhodla sa, že sa oblečie. preto si na treťom článku od konca a potom na každom ďalšom treťom článku obliekla ponožku na ľavú nôžku. Podobne si na
Stonožka Mirka pozostáva z hlavy a niekoľkých článkov, na každom článku má jeden pár nôh. Keď sa ochladilo, rozhodla sa, že sa oblečie. preto si na treťom článku od konca a potom na každom ďalšom treťom článku obliekla ponožku na ľavú nôžku. Podobne si na - Zvonkohra MO - Z5 - 1 - 66
 Zvonkohra na nádvorí hrá o každej celej hodine krátku skladbu, a to počínajúc 8. a končiac 22. hodinou. Skladieb je celkom osemnásť, o celej hodine sa hrá vždy iba jedna a po odohraní všetkých osemnástich sa začína v rovnakom poradí znova. Oľga a Ľuboš bo
Zvonkohra na nádvorí hrá o každej celej hodine krátku skladbu, a to počínajúc 8. a končiac 22. hodinou. Skladieb je celkom osemnásť, o celej hodine sa hrá vždy iba jedna a po odohraní všetkých osemnástich sa začína v rovnakom poradí znova. Oľga a Ľuboš bo - MO-Z5-3-66
 Na obrázku je štvorcová dlaždica so stranou dĺžky 10 dm, ktorá je zložená zo štyroch zhodných obdĺžnikov a malého štvorca. Obvod malého štvorca je päťkrát menší ako obvod celej dlaždice. Určte rozmery obdĺžnikov.
Na obrázku je štvorcová dlaždica so stranou dĺžky 10 dm, ktorá je zložená zo štyroch zhodných obdĺžnikov a malého štvorca. Obvod malého štvorca je päťkrát menší ako obvod celej dlaždice. Určte rozmery obdĺžnikov. - Logický príklad
 V trojposchodovom dome bývajú štyria chlapci. Každý býva na inom poschodí. Vieme o nich toto: - Jozef je filatelista - Viktor nebýva na najvyššom poschodí a nevie fotografovať - Ivan sa priatelí z fotoamatérom z prízemia - modelár z tretieho poschodia sa
V trojposchodovom dome bývajú štyria chlapci. Každý býva na inom poschodí. Vieme o nich toto: - Jozef je filatelista - Viktor nebýva na najvyššom poschodí a nevie fotografovať - Ivan sa priatelí z fotoamatérom z prízemia - modelár z tretieho poschodia sa - Z6–I–2
 Pán Kockorád vlastnil záhradu obdĺžnikového tvaru, na ktorej postupne dláždil chodníky z jednej strany na druhú. Chodníky boli rovnako široké, križovali sa na dvoch miestach a už vydláždená plocha sa pri ďalšom dláždení preskakovala. Keď pán Kockorád vydl
Pán Kockorád vlastnil záhradu obdĺžnikového tvaru, na ktorej postupne dláždil chodníky z jednej strany na druhú. Chodníky boli rovnako široké, križovali sa na dvoch miestach a už vydláždená plocha sa pri ďalšom dláždení preskakovala. Keď pán Kockorád vydl
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
