Vyjadrenie neznámej zo vzorca + matematická olympiáda - príklady a úlohy
Počet nájdených príkladov: 23
- Trojuholníka 82724
 Pravouhlý trojuholník má obsah 36 cm². V ňom je umiestnený štvorec tak, že dve strany štvorca sú časťami dvoch strán trojuholníka a jeden vrchol štvorca je v tretine najdlhšej strany. Určite obsah tohto štvorca.
Pravouhlý trojuholník má obsah 36 cm². V ňom je umiestnený štvorec tak, že dve strany štvorca sú časťami dvoch strán trojuholníka a jeden vrchol štvorca je v tretine najdlhšej strany. Určite obsah tohto štvorca. - Trojuholníka 81293
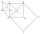 Na obrázku sú znázornené štvorce ABCD, EFCA, CHCE a IJHE. Body S, B, F a G sú po rade stredy týchto štvorcov. Úsečka AC je dlhá 1 cm. Určite obsah trojuholníka IJS. Prosím pomôžte...
Na obrázku sú znázornené štvorce ABCD, EFCA, CHCE a IJHE. Body S, B, F a G sú po rade stredy týchto štvorcov. Úsečka AC je dlhá 1 cm. Určite obsah trojuholníka IJS. Prosím pomôžte... - MO z9 2022
 Sú dané dva zhodné rovnostranné trojuholníky ABC a BDE tak, že veľkosť uhla ABD je väčšia ako 120° a menšia ako 180° a body C, E ležia v rovnakej polrovine vymedzenej priamkou AD. Priesečník CD a AE je označený F. Určte veľkosť uhla AFD.
Sú dané dva zhodné rovnostranné trojuholníky ABC a BDE tak, že veľkosť uhla ABD je väčšia ako 120° a menšia ako 180° a body C, E ležia v rovnakej polrovine vymedzenej priamkou AD. Priesečník CD a AE je označený F. Určte veľkosť uhla AFD. - Dedecek 63074
 Môj jediný syn sa narodil keď som mal 37 rokov. to bolo práve 32 rokov po smrti dedka a ten zomrel vo svojich 64 rokoch. Dedecek bol o 12 rokov starší ako babička, brali sa v roku 1947 práve keď babičke bolo 18 rokov. V ktorom roku sa narodil môj syn?
Môj jediný syn sa narodil keď som mal 37 rokov. to bolo práve 32 rokov po smrti dedka a ten zomrel vo svojich 64 rokoch. Dedecek bol o 12 rokov starší ako babička, brali sa v roku 1947 práve keď babičke bolo 18 rokov. V ktorom roku sa narodil môj syn? - MO Z7–I–6 2021
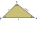 V trojuholníku ABC leží na strane AC bod D a na strane BC bod E. Veľkosti uhlov ABD, BAE, CAE a CBD sú postupne 30°, 60°, 20° a 30°. určte veľkosť uhla AED.
V trojuholníku ABC leží na strane AC bod D a na strane BC bod E. Veľkosti uhlov ABD, BAE, CAE a CBD sú postupne 30°, 60°, 20° a 30°. určte veľkosť uhla AED. - Dva prístavy
 Medzi prístavy Mumraj a Zmätok pendlujú po rovnakej trase dve lode. V prístavoch trávia zanedbateľný čas, hneď sa otáčajú a pokračujú v plavbe. Ráno v rovnaký okamih vypláva modrá loď z prístavu Mumraj a zelená loď z prístavu Zmätok. Prvýkrát sa lode míňa
Medzi prístavy Mumraj a Zmätok pendlujú po rovnakej trase dve lode. V prístavoch trávia zanedbateľný čas, hneď sa otáčajú a pokračujú v plavbe. Ráno v rovnaký okamih vypláva modrá loď z prístavu Mumraj a zelená loď z prístavu Zmätok. Prvýkrát sa lode míňa - Z6–I–5 MO 2019
 Útvar na obrázku vznikol tak, že z veľkého kríža bol vystrihnutý malý kríž. Každý z týchto krížov môže byť zložený z piatich zhodných štvorcov, pričom strany malých štvorcov sú polovičné vzhľadom na strany veľkých štvorcov. Obsah sivého útvaru je 45 cm².
Útvar na obrázku vznikol tak, že z veľkého kríža bol vystrihnutý malý kríž. Každý z týchto krížov môže byť zložený z piatich zhodných štvorcov, pričom strany malých štvorcov sú polovičné vzhľadom na strany veľkých štvorcov. Obsah sivého útvaru je 45 cm². - Z8–I–3 MO 2019
 Vendelín býva medzi dvoma zastávkami autobusu, a to v troch osminách ich vzdialenosti. Dnes vyrazil z domu a zistil, že či by utekal k jednej, alebo druhej zastávke, dorazil by na zastávku súčasne s autobusom. Priemerná rýchlosť autobusu je 60 km/h. Akou
Vendelín býva medzi dvoma zastávkami autobusu, a to v troch osminách ich vzdialenosti. Dnes vyrazil z domu a zistil, že či by utekal k jednej, alebo druhej zastávke, dorazil by na zastávku súčasne s autobusom. Priemerná rýchlosť autobusu je 60 km/h. Akou - Z9 – I – 5 MO 2018
 Peter a Ivan vytvárali dekorácie z navzájom zhodných bielych kruhov. Peter použil štyri kruhy, ktoré položil tak, že sa každý dotýkal dvoch iných kruhov. Medzi ne potom vložil iný kruh, ktorý sa dotýkal všetkých štyroch bielych kruhov, a ten vyfarbil červ
Peter a Ivan vytvárali dekorácie z navzájom zhodných bielych kruhov. Peter použil štyri kruhy, ktoré položil tak, že sa každý dotýkal dvoch iných kruhov. Medzi ne potom vložil iný kruh, ktorý sa dotýkal všetkých štyroch bielych kruhov, a ten vyfarbil červ - Z5–I–1 MO 2018
 Miška má päť pasteliek. Vojto ich má menej ako Miška. Vendelín ich má toľko, koľko Miška a Vojto spolu. Všetci traja spolu majú sedemkrát viac pasteliek, ako má Vojto. Koľko pasteliek má Vendelín?
Miška má päť pasteliek. Vojto ich má menej ako Miška. Vendelín ich má toľko, koľko Miška a Vojto spolu. Všetci traja spolu majú sedemkrát viac pasteliek, ako má Vojto. Koľko pasteliek má Vendelín? - Z7-1-3 MO 2018
 Dedo pripravil pre svojich šesť vnúčat kôpku lieskových orieškov s tým, nech si ich nejako rozoberú. Prvý prišiel Adam, odpočítal si polovicu, pribral si ešte jeden oriešok a odišiel. Rovnako sa zachoval druhý Bob, tretí Cyril, štvrtý Dano aj piaty Edo. I
Dedo pripravil pre svojich šesť vnúčat kôpku lieskových orieškov s tým, nech si ich nejako rozoberú. Prvý prišiel Adam, odpočítal si polovicu, pribral si ešte jeden oriešok a odišiel. Rovnako sa zachoval druhý Bob, tretí Cyril, štvrtý Dano aj piaty Edo. I - Z9 – I – 2 MO 2018
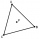 V rovnostrannom trojuholníku ABC je K stredom strany AB, bod L leží v tretine strany BC bližšie bodu C a bod M leží v tretine strany AC bližšie bodu A. Určte, akú časť obsahu trojuholníka ABC zaberá trojuholník KLM.
V rovnostrannom trojuholníku ABC je K stredom strany AB, bod L leží v tretine strany BC bližšie bodu C a bod M leží v tretine strany AC bližšie bodu A. Určte, akú časť obsahu trojuholníka ABC zaberá trojuholník KLM. - Adam mal
 Adam mal tri zhodné obdĺžniky. Priložil ich k sebe a dostal obdĺžnik s obvodom 50 cm. Potom ich priložil inak a dostal obdĺžnik s väčším obvodom. Vypočítaj jeho obvod.
Adam mal tri zhodné obdĺžniky. Priložil ich k sebe a dostal obdĺžnik s obvodom 50 cm. Potom ich priložil inak a dostal obdĺžnik s väčším obvodom. Vypočítaj jeho obvod. - Z7-I-5 MO 2017
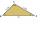 Prokop zostrojil trojuholník ABC, ktorého vnútorný uhol pri vrchole A bol väčší ako 60° a vnútorný uhol pri vrchole B bol menší ako 60°. Juraj narysoval v polrovine určenej priamkou AB a bodom C bod D, a to tak, že trojuholník ABD bol rovnostranný. Potom
Prokop zostrojil trojuholník ABC, ktorého vnútorný uhol pri vrchole A bol väčší ako 60° a vnútorný uhol pri vrchole B bol menší ako 60°. Juraj narysoval v polrovine určenej priamkou AB a bodom C bod D, a to tak, že trojuholník ABD bol rovnostranný. Potom - Z9-I-5 MO 2017 obdlžník
 Vnútri obdlžníka ABCD ležia body M a N. Strana AB je 22 cm a kružnica opísaná trojuholníku AND má polomer 10cm a úsečky MA, MD, MN, NB a NC sú navzájom zhodné. Určite dĺžku strany BC.
Vnútri obdlžníka ABCD ležia body M a N. Strana AB je 22 cm a kružnica opísaná trojuholníku AND má polomer 10cm a úsečky MA, MD, MN, NB a NC sú navzájom zhodné. Určite dĺžku strany BC. - Z7–I–2 MO 2017
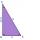 Dané sú dve dvojice rovnobežných priamok AB k CD a AC k BD. Bod E leží na priamke BD, bod F je stredom úsečky BD, bod G je stredom úsečky CD a obsah trojuholníka ACE je 20 cm². Určte obsah trojuholníka DFG.
Dané sú dve dvojice rovnobežných priamok AB k CD a AC k BD. Bod E leží na priamke BD, bod F je stredom úsečky BD, bod G je stredom úsečky CD a obsah trojuholníka ACE je 20 cm². Určte obsah trojuholníka DFG. - MO Z6–I–1 - 2017 - Anička
 Anička a Blanka si napísali každá jedno dvojciferné číslo, ktoré začínalo sedmičkou. Dievčatá si zvolili rôzne čísla. Potom každá medzi obe cifry vložila nulu, takže im vzniklo trojciferné číslo. Od neho každá odčítala svoje pôvodné dvojciferné číslo. Výs
Anička a Blanka si napísali každá jedno dvojciferné číslo, ktoré začínalo sedmičkou. Dievčatá si zvolili rôzne čísla. Potom každá medzi obe cifry vložila nulu, takže im vzniklo trojciferné číslo. Od neho každá odčítala svoje pôvodné dvojciferné číslo. Výs - MO Z9–I–1 2017
 Vekový priemer všetkých ľudí na oslave bol rovný počtu prítomných. Po odchode jednej osoby, ktorej bolo 29 rokov, bol vekový priemer zase rovný počtu prítomných. Koľko ľudí bolo pôvodne na oslave?
Vekový priemer všetkých ľudí na oslave bol rovný počtu prítomných. Po odchode jednej osoby, ktorej bolo 29 rokov, bol vekový priemer zase rovný počtu prítomných. Koľko ľudí bolo pôvodne na oslave? - MO - bikvadrát
 Nájdite najväčšie prirodzené číslo d, ktoré má tú vlastnosť, že pre ľubovoľné prirodzené číslo n je hodnota výrazu V(n)=n4+11n²−12 deliteľná číslom d.
Nájdite najväčšie prirodzené číslo d, ktoré má tú vlastnosť, že pre ľubovoľné prirodzené číslo n je hodnota výrazu V(n)=n4+11n²−12 deliteľná číslom d. - Celočíselnými 4445
 Nájdete všetky trojčleny P(x) = a * x² + b * x + c s celočíselnými koeficientmi a, b a c, pre ktoré platí P(1) < P(2) < P(3) a zároveň ((P(1)) ² + ((P(2)) ² + ((P(3)) ² = 22).
Nájdete všetky trojčleny P(x) = a * x² + b * x + c s celočíselnými koeficientmi a, b a c, pre ktoré platí P(1) < P(2) < P(3) a zároveň ((P(1)) ² + ((P(2)) ² + ((P(3)) ² = 22).
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
