Kruh, kružnica - 9. ročník - príklady a úlohy
Počet nájdených príkladov: 433
- Opísaná kružnica
 Vypočítajte polomer kružnice opísaneho trojuholníku, ktorý má rozmery strán 8, 10 a 14cm.
Vypočítajte polomer kružnice opísaneho trojuholníku, ktorý má rozmery strán 8, 10 a 14cm. - Dve tetivy
 Dané sú dve úsečky rôznych dĺžok. Zostrojte kružnicu k tak, aby obe úsečky boli jej tetivami.
Dané sú dve úsečky rôznych dĺžok. Zostrojte kružnicu k tak, aby obe úsečky boli jej tetivami. - Tetiva - uhol
 Je daná kružnica k so stredom v bode S a polomerom 6 cm. Vypočítaj veľkosť stredového uhla, ktorý patí tetive dlhej 10 cm.
Je daná kružnica k so stredom v bode S a polomerom 6 cm. Vypočítaj veľkosť stredového uhla, ktorý patí tetive dlhej 10 cm. - Daný je 9
 Daný je rovnoramenný trojuholník, ktorého základňa je 8cm a ramená majú dĺžku 15 cm. Vypočítaj obsah trojuholníka a polomer vpísanej a opísanej kružnice.
Daný je rovnoramenný trojuholník, ktorého základňa je 8cm a ramená majú dĺžku 15 cm. Vypočítaj obsah trojuholníka a polomer vpísanej a opísanej kružnice.
- Na kruhovom 2
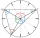 Na kruhovom ciferníku hodín navzájom pospájame body prislúchajúce číslam 2,5,9, čím vznikne trojuholník. Vypočítajte veľkosti všetkých vnútorných uhlov.
Na kruhovom ciferníku hodín navzájom pospájame body prislúchajúce číslam 2,5,9, čím vznikne trojuholník. Vypočítajte veľkosti všetkých vnútorných uhlov. - Koľko 156
 Koľko meria najkratšia vzdialenosť po povrchu glóbusu v mierke 1:1 000 000 z rovníka na severný pól?
Koľko meria najkratšia vzdialenosť po povrchu glóbusu v mierke 1:1 000 000 z rovníka na severný pól? - Zisti 9
 Zisti či kruh s obsahom 38,5cm² vojde do obdlznika s rozmermi 110mm a 65mm
Zisti či kruh s obsahom 38,5cm² vojde do obdlznika s rozmermi 110mm a 65mm - Archeologovia 2
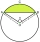 Archeológovia potrebujú zistiť veľkosť nádoby, ak nájdeny črep bol v tvare kruhového odseku s dĺžkou 12 cm a výškou 3 cm. Aký je obsah tohto odseku?
Archeológovia potrebujú zistiť veľkosť nádoby, ak nájdeny črep bol v tvare kruhového odseku s dĺžkou 12 cm a výškou 3 cm. Aký je obsah tohto odseku? - Gotický
 Gotický štvorlístok je ornament, v ktorom sú do väčšej kružnice vpísané štyri rovnaké dotýkajúce sa menšie kružnice, ako vidíte na obrázku. Polomer veľkej kružnice je jeden meter. Vypočítajte v metroch polomer menšej kružnice.
Gotický štvorlístok je ornament, v ktorom sú do väčšej kružnice vpísané štyri rovnaké dotýkajúce sa menšie kružnice, ako vidíte na obrázku. Polomer veľkej kružnice je jeden meter. Vypočítajte v metroch polomer menšej kružnice.
- Tetivka
 Vypočítaj vzdialenosť tetivy dlhej 19 cm od stredu kružnice s priemerom 28 cm.
Vypočítaj vzdialenosť tetivy dlhej 19 cm od stredu kružnice s priemerom 28 cm. - Vzdialenosť 83356
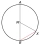 Vzdialenosť tetivy od stredu je 6 cm. Stredový uhol je 60 °. Vypočítajte plošný obsah kruhovej úseče.
Vzdialenosť tetivy od stredu je 6 cm. Stredový uhol je 60 °. Vypočítajte plošný obsah kruhovej úseče. - Kruh odsek/úsek
 Kruh s priemerom 30 cm je preťať tetivou t = 16 cm. Vypočítajte obvod a obsah menšieho odseku.
Kruh s priemerom 30 cm je preťať tetivou t = 16 cm. Vypočítajte obvod a obsah menšieho odseku. - Uhlopriečkou 83307
 Uhlopriečkou rezu DBFH pravidelného štvorbokého hranola ABCDEFGH je vpísaný kruh s priemerom 8 cm. Aký je objem hranola.
Uhlopriečkou rezu DBFH pravidelného štvorbokého hranola ABCDEFGH je vpísaný kruh s priemerom 8 cm. Aký je objem hranola. - Rozkrojila 83127
 Katka si objednala tortu v tvare valca s objemom 15,7l. Skladá sa z dvoch poschodí. Objem horného poschodia je 4x menší ako objem dolného poschodia. Výška oboch poschodí rovnaká a je rovná polomeru horného poschodia torty. Katka rozkrojila tortu kolmo k p
Katka si objednala tortu v tvare valca s objemom 15,7l. Skladá sa z dvoch poschodí. Objem horného poschodia je 4x menší ako objem dolného poschodia. Výška oboch poschodí rovnaká a je rovná polomeru horného poschodia torty. Katka rozkrojila tortu kolmo k p
- Vytieňovanej 83069
 Do kruhu s polomerom 4 cm je vpísaný rovnostranný trojuholník. Nájdite oblasť vytieňovanej oblasti.
Do kruhu s polomerom 4 cm je vpísaný rovnostranný trojuholník. Nájdite oblasť vytieňovanej oblasti. - Betónová 82858
 Betónová rúra je dlhá 1,0 m. Jeho vnútorný a vonkajší priemer je 60 cm a 75 cm. Aký objem betónu (metre kubické) je potrebný na výrobu 25 ks rúry?
Betónová rúra je dlhá 1,0 m. Jeho vnútorný a vonkajší priemer je 60 cm a 75 cm. Aký objem betónu (metre kubické) je potrebný na výrobu 25 ks rúry? - Vyfarbená 82623
 Štvorec na obrázku má dĺžku strany 6cm. Koľko percent z obsahu tvorí vyfarbená časť?
Štvorec na obrázku má dĺžku strany 6cm. Koľko percent z obsahu tvorí vyfarbená časť? - Percentuálny 81971
 Polomer kruhu sa zväčší o 5 %. Aký je percentuálny nárast ich obvodovej plochy?
Polomer kruhu sa zväčší o 5 %. Aký je percentuálny nárast ich obvodovej plochy? - Opracovával 81914
 Stolár opracovával rotačný valec s polomerom podstavy 2,5 dm a výškou 2 dm. Rovnomerným brúsením zmenšil polomer o 1cm, výška valca bola zachovaná. Vypočítaj, o koľko percent sa zmenšil obsah valca.
Stolár opracovával rotačný valec s polomerom podstavy 2,5 dm a výškou 2 dm. Rovnomerným brúsením zmenšil polomer o 1cm, výška valca bola zachovaná. Vypočítaj, o koľko percent sa zmenšil obsah valca.
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
