Derivácia - príklady
Pokyny: Vyriešte každú úlohu starostlivo a ukážte svoje celé riešenie. Ak je to vhodné, vykonajte skúšku správnosti riešenia.Počet nájdených príkladov: 50
- Zrýchlenie 9
 Zrýchlenie hmotného bodu pri jeho priamočiarom pohybe rovnomerne klesá zo začiatočnej hodnoty a0 = 10 m/s² v čase t0 = 0 na nulovú hodnotu počas 20 s. Aká je rýchlosť hmotného bodu v čase t1 = 20 s a akú dráhu za ten čas hmotný bod prešiel, keď v čase t0
Zrýchlenie hmotného bodu pri jeho priamočiarom pohybe rovnomerne klesá zo začiatočnej hodnoty a0 = 10 m/s² v čase t0 = 0 na nulovú hodnotu počas 20 s. Aká je rýchlosť hmotného bodu v čase t1 = 20 s a akú dráhu za ten čas hmotný bod prešiel, keď v čase t0 - X=10t^2-5t 82397
 Poloha hmotného bodu, ktorý sa pohybuje pozdĺž osi x, je daná vzťahom x=10t²-5t. Vyjadrite jeho rýchlosť a zrýchlenie.
Poloha hmotného bodu, ktorý sa pohybuje pozdĺž osi x, je daná vzťahom x=10t²-5t. Vyjadrite jeho rýchlosť a zrýchlenie. - (1/3)*PI*h*h*(3R-h) 82080
 Mám stan v tvare guľovej čiapky (guľový odsek). Predpokladajme, že chceme, aby objem bol 4 metre kubické, aby sa tam vyspali dvaja alebo traja ľudia. Predpokladajme, že materiál tvoriaci kupolu desiatky je dvakrát drahší na štvorec ako materiál dotýkajúci
Mám stan v tvare guľovej čiapky (guľový odsek). Predpokladajme, že chceme, aby objem bol 4 metre kubické, aby sa tam vyspali dvaja alebo traja ľudia. Predpokladajme, že materiál tvoriaci kupolu desiatky je dvakrát drahší na štvorec ako materiál dotýkajúci - Spotreba
 Spotreba benzínu na kilometer M (jednotka kilometer na liter) auta Dodge Caliber je modelovaná funkciou M(s) = - 1/28s² + 3s- 31 Akú má auto najlepšiu spotrebu (benzínové kilometre) a akú rýchlosť dosiahne?
Spotreba benzínu na kilometer M (jednotka kilometer na liter) auta Dodge Caliber je modelovaná funkciou M(s) = - 1/28s² + 3s- 31 Akú má auto najlepšiu spotrebu (benzínové kilometre) a akú rýchlosť dosiahne? - X^3+x^2-x-1/x^2-2x-3 80584
 Na riešenie použite L Hopitalovo pravidlo (i) Lim x²+5x-14/x²-5x+6 X—>2 (ii) Lim x³+x²-x-1/x²-2x-3 X—>3
Na riešenie použite L Hopitalovo pravidlo (i) Lim x²+5x-14/x²-5x+6 X—>2 (ii) Lim x³+x²-x-1/x²-2x-3 X—>3 - Vzdialenosť 75844
 Ak je pohyb častice opísaný vzťahom a(t) = 7t³ + 2 m/s² a počiatočná rýchlosť pohybu je nulová, keď t = 0 a vzdialenosť je 2 m, t = 0,5 s . Určte rýchlosť a polohu, keď t = 10s.
Ak je pohyb častice opísaný vzťahom a(t) = 7t³ + 2 m/s² a počiatočná rýchlosť pohybu je nulová, keď t = 0 a vzdialenosť je 2 m, t = 0,5 s . Určte rýchlosť a polohu, keď t = 10s. - Diferencovateľné 74984
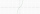 A). Načrtnite graf funkcie f(x)=x * abs (x) = x * |x| b). Pre aké hodnoty x je f(x) diferencovateľné c). Nájsť F(x)
A). Načrtnite graf funkcie f(x)=x * abs (x) = x * |x| b). Pre aké hodnoty x je f(x) diferencovateľné c). Nájsť F(x) - Priesečníkov 74874
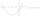 Rovnica krivky C je y=2x² - 8x +9 a rovnica priamky L je x + y=3. (1) Nájdite x-ové súradnice priesečníkov L a C. ii) ukázať, že jeden z týchto bodov je tiež
Rovnica krivky C je y=2x² - 8x +9 a rovnica priamky L je x + y=3. (1) Nájdite x-ové súradnice priesečníkov L a C. ii) ukázať, že jeden z týchto bodov je tiež - F(x)=(e^x)/((e^x)+1) 70464
 Funkcie: f(x)=xtanx f(x)=(e^x)/((e^x)+1) Nájsť; i) vertikálne a horizontálne asymptoty iii) intervaly poklesu a rastu iii) Miestne maximá a miestne minimá iv) interval konkávnosti a inflexie. A načrtnite graf.
Funkcie: f(x)=xtanx f(x)=(e^x)/((e^x)+1) Nájsť; i) vertikálne a horizontálne asymptoty iii) intervaly poklesu a rastu iii) Miestne maximá a miestne minimá iv) interval konkávnosti a inflexie. A načrtnite graf. - S(t)=500-5t^2 70144
 Muž zhodil cent z vrcholu 500 metrov vysokej budovy. Po t sekundách cent klesol o vzdialenosť s metrov, kde s(t)=500-5t² . Určte priemernú rýchlosť medzi 1 s a 5 s.
Muž zhodil cent z vrcholu 500 metrov vysokej budovy. Po t sekundách cent klesol o vzdialenosť s metrov, kde s(t)=500-5t² . Určte priemernú rýchlosť medzi 1 s a 5 s. - Na lúke
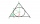 Na lúke pristála kozmická loď v tvare gule s priemerom 6 m. Aby nepútali pozornosť, zakryli ju Marťankovia strechou v tvare pravidelného kužeľa. Ako vysoká bude táto strecha, aby spotreba krytiny bola minimálna?
Na lúke pristála kozmická loď v tvare gule s priemerom 6 m. Aby nepútali pozornosť, zakryli ju Marťankovia strechou v tvare pravidelného kužeľa. Ako vysoká bude táto strecha, aby spotreba krytiny bola minimálna? - Megapizza
 Megapizza bude rozdelená medzi 100 ľudí. 1. dostane 1%, 2. 2% zo zvyšku, 3. 3% zo zvyšku atď. Posledné 100. 100% zo zvyšku. Ktorý človek dostal najväčšiu porciu?
Megapizza bude rozdelená medzi 100 ľudí. 1. dostane 1%, 2. 2% zo zvyšku, 3. 3% zo zvyšku atď. Posledné 100. 100% zo zvyšku. Ktorý človek dostal najväčšiu porciu? - Ivan a
 Ivan a Katka objavili na dovolenke pravidelný ihlan, ktorého podstavou bol štvorec so stranou 230 m a ktorého výška bola rovná polomeru kruhu s rovnakým obsahom ako podstavný štvorec. Katka označila vrcholy štvorca ABCD. Ivan vyznačil na priamke spájajúce
Ivan a Katka objavili na dovolenke pravidelný ihlan, ktorého podstavou bol štvorec so stranou 230 m a ktorého výška bola rovná polomeru kruhu s rovnakým obsahom ako podstavný štvorec. Katka označila vrcholy štvorca ABCD. Ivan vyznačil na priamke spájajúce - Smernica
 Ktorá z funkcii je rastúca? a) y=2-x b) y=20 c) y=(x+2). (-5) d) y=x-2
Ktorá z funkcii je rastúca? a) y=2-x b) y=20 c) y=(x+2). (-5) d) y=x-2 - Plášť
 Plášť kužeľa je vytvorený zvinutím kruhového výseku s polomerom 1. Pre aký stredový uhol daného kruhového výseku bude objem vzniknutého kužeľa maximálnu?
Plášť kužeľa je vytvorený zvinutím kruhového výseku s polomerom 1. Pre aký stredový uhol daného kruhového výseku bude objem vzniknutého kužeľa maximálnu? - 352/5000
Strelec
 352/5000 Strelec strieľa do terča, pričom predpokladáme, že jednotlivé výstrely sú navzájom nezávislé a pravdepodobnosť zásahu je u každého z nich 0,2. Strelec strieľa tak dlho, kým prvýkrát terč nezasiahne, potom streľbu ukončí. (A) Aký je najpravdepodob
352/5000 Strelec strieľa do terča, pričom predpokladáme, že jednotlivé výstrely sú navzájom nezávislé a pravdepodobnosť zásahu je u každého z nich 0,2. Strelec strieľa tak dlho, kým prvýkrát terč nezasiahne, potom streľbu ukončí. (A) Aký je najpravdepodob - Derivačný príklad
 Súčet dvoch čísel je 12. Nájdite tieto čísla, ak: a) Súčet ich tretích mocnín je minimálna. b) Súčin jedného s treťou mocninou druhého je maximálna. c) Obe sú kladné a súčin jedného s druhou mocninou druhého je maximálna.
Súčet dvoch čísel je 12. Nájdite tieto čísla, ak: a) Súčet ich tretích mocnín je minimálna. b) Súčin jedného s treťou mocninou druhého je maximálna. c) Obe sú kladné a súčin jedného s druhou mocninou druhého je maximálna. - Simplexová metóda
 Reťazec obchodných domov plánuje investovať do televíznej reklamy až 24 000 Eur. Všetky reklamné spoty budú umiestnené na televíznej stanici, na ktorej odvysielanie 30 sekundového spotu stojí 1000 Eur a sleduje ho 14 000 potenciálnych zákazníkov, počas pr
Reťazec obchodných domov plánuje investovať do televíznej reklamy až 24 000 Eur. Všetky reklamné spoty budú umiestnené na televíznej stanici, na ktorej odvysielanie 30 sekundového spotu stojí 1000 Eur a sleduje ho 14 000 potenciálnych zákazníkov, počas pr - Poklad
 Skauti majú stan v tvare pravidelného štvorbokého ihlanu so stranou podstavy 4 m a výške 3 m. Do stanu potrebujú schovať valcovú nádobu s tajným pokladom. Určte polomer r (a výšku h) nádoby tak, aby mohli schovať čo nejobjemnější poklad.
Skauti majú stan v tvare pravidelného štvorbokého ihlanu so stranou podstavy 4 m a výške 3 m. Do stanu potrebujú schovať valcovú nádobu s tajným pokladom. Určte polomer r (a výšku h) nádoby tak, aby mohli schovať čo nejobjemnější poklad. - Mimozemská loď
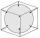 Mimozemská loď má tvar gule o polomere r = 3000m a jej posádka potrebuje loďou odviezť nazbieraný výskumný materiál v boxe v tvare kvádra so štvorcovou podstavou. Určte dĺžku podstavy a (a výšku h) tak, aby mal box najväčší možný objem.
Mimozemská loď má tvar gule o polomere r = 3000m a jej posádka potrebuje loďou odviezť nazbieraný výskumný materiál v boxe v tvare kvádra so štvorcovou podstavou. Určte dĺžku podstavy a (a výšku h) tak, aby mal box najväčší možný objem.
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
