Konštrukčné úlohy + matematická olympiáda - príklady a úlohy
Počet nájdených príkladov: 9
- Z8 – I – 1 MO 2019
 Zostrojte kosoštvorec ABCD tak, aby jeho uhlopriečka BD mala veľkosť 8 cm a vzdialenosť vrcholu B od priamky AD bola 5 cm. Určte všetky možnosti.
Zostrojte kosoštvorec ABCD tak, aby jeho uhlopriečka BD mala veľkosť 8 cm a vzdialenosť vrcholu B od priamky AD bola 5 cm. Určte všetky možnosti. - C-I-2 2018 MO
 Na strane AB trojuholníka ABC sú dané body D a E tak, že |AD| = |DE| = |EB|. Body A a B sú postupne stredmi úsečiek CF a CG. Priamka CD pretína priamku FB v bode I a priamka CE pretína priamku AG v bode J. Dokážte, že priesečník priamok AI a BJ leží na pr
Na strane AB trojuholníka ABC sú dané body D a E tak, že |AD| = |DE| = |EB|. Body A a B sú postupne stredmi úsečiek CF a CG. Priamka CD pretína priamku FB v bode I a priamka CE pretína priamku AG v bode J. Dokážte, že priesečník priamok AI a BJ leží na pr - Z7-1-6 MO 2018
 Daný je rovnoramenný pravouhlý trojuholník ABS so základňou AB. Na kružnici, ktorá má stred v bode S a prechádza bodmi A a B, leží bod C tak, že trojuholník ABC je rovnoramenný. Určte, koľko bodov C vyhovuje uvedeným podmienkam, a všetky také body zostroj
Daný je rovnoramenný pravouhlý trojuholník ABS so základňou AB. Na kružnici, ktorá má stred v bode S a prechádza bodmi A a B, leží bod C tak, že trojuholník ABC je rovnoramenný. Určte, koľko bodov C vyhovuje uvedeným podmienkam, a všetky také body zostroj - Rovnoramenný - Z7–I–5
 Je daný trojuholník ABC so stranami /AB/ = 3 cm, /BC/ = 10 cm a uhlom ABC = 120°. Narysujte všetky body X tak, aby platilo, že trojuholník BCX je rovnoramenný a súčasne trojuholník ABX je rovnoramenný so základňou AB.
Je daný trojuholník ABC so stranami /AB/ = 3 cm, /BC/ = 10 cm a uhlom ABC = 120°. Narysujte všetky body X tak, aby platilo, že trojuholník BCX je rovnoramenný a súčasne trojuholník ABX je rovnoramenný so základňou AB. - Z9–I–1
 Vo všetkých deviatich poliach obrazca majú byť vyplnené prirodzené čísla tak, aby platilo: • každé z čísel 2, 4, 6 a 8 je použité aspoň raz, • štyri z polí vnútorného štvorca obsahujú súčiny čísel zo susediacich polí vonkajšieho štvorca, • v kruhu je súče
Vo všetkých deviatich poliach obrazca majú byť vyplnené prirodzené čísla tak, aby platilo: • každé z čísel 2, 4, 6 a 8 je použité aspoň raz, • štyri z polí vnútorného štvorca obsahujú súčiny čísel zo susediacich polí vonkajšieho štvorca, • v kruhu je súče - Z9–I–6 MRAK
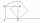 Je daná úsečka AB dĺžky 12 cm, na ktorej je jednou stranou položený štvorec MRAK so stranou dĺžky 2 cm, viď obrázok. MRAK sa postupne preklápa po úsečke AB, pričom bod R zanecháva na papieri stopu. Narysujte celú stopu bodu R, kým štvorec nezaobíde úsečku
Je daná úsečka AB dĺžky 12 cm, na ktorej je jednou stranou položený štvorec MRAK so stranou dĺžky 2 cm, viď obrázok. MRAK sa postupne preklápa po úsečke AB, pričom bod R zanecháva na papieri stopu. Narysujte celú stopu bodu R, kým štvorec nezaobíde úsečku - Šesťuholník nepravidelný
 Na obrázku je štvorec ABCD, štvorec EFGD a obdĺžnik HIJD. Body J a G ležia na strane CD, pričom platí |DJ| < |DG| a body H a E ležia na strane DA, pričom platí /DH/ < /DE/. Ďalej vieme, že/DJ/ = /GC/. Šesťuholník ABCGFE má obvod 96 cm, šesťuholník E
Na obrázku je štvorec ABCD, štvorec EFGD a obdĺžnik HIJD. Body J a G ležia na strane CD, pričom platí |DJ| < |DG| a body H a E ležia na strane DA, pričom platí /DH/ < /DE/. Ďalej vieme, že/DJ/ = /GC/. Šesťuholník ABCGFE má obvod 96 cm, šesťuholník E - Katka MO
 Katka narysovala trojuholník ABC. Stred strany AB si označila ako X a stred strany AC ako Y. Na strane BC chce nájsť taký bod Z, aby obsah štvoruholníka AXZY bol čo najväčší. Akú časť trojuholníka ABC môže maximálne zaberať štvoruholník AXZY?
Katka narysovala trojuholník ABC. Stred strany AB si označila ako X a stred strany AC ako Y. Na strane BC chce nájsť taký bod Z, aby obsah štvoruholníka AXZY bol čo najväčší. Akú časť trojuholníka ABC môže maximálne zaberať štvoruholník AXZY? - Štvorcová sieť
 Štvorcová sieť sa skladá zo štvorca so stranou dĺžky 1cm. Narysujte do nej aspoň tri rôzne obrazce také, aby každý mal obsah 6 cm² a obvod 12cm a aby ich strany splývali s priamkami siete.
Štvorcová sieť sa skladá zo štvorca so stranou dĺžky 1cm. Narysujte do nej aspoň tri rôzne obrazce také, aby každý mal obsah 6 cm² a obvod 12cm a aby ich strany splývali s priamkami siete.
Ospravedlňujeme sa, ale v tejto kategórií nie je veľa príkladov.
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
