Príklady pre stredoškolákov - strana 101 z 206
Počet nájdených príkladov: 4106
- Predĺženie obdĺžnika
 Obdĺžnik budeme opakovane zväčšovať tak, že stranu, ktorá je v danom okamihu kratšia, predĺžime o 3 cm a dlhšiu stranu len o 1 cm. Po treťom predĺžení sa vytvorí obdĺžnik s rozmermi 11 cm a 12 cm. 1. Určite rozmery pôvodného obdĺžnika. 2. Určite rozmery o
Obdĺžnik budeme opakovane zväčšovať tak, že stranu, ktorá je v danom okamihu kratšia, predĺžime o 3 cm a dlhšiu stranu len o 1 cm. Po treťom predĺžení sa vytvorí obdĺžnik s rozmermi 11 cm a 12 cm. 1. Určite rozmery pôvodného obdĺžnika. 2. Určite rozmery o - Na obrazovke
 Na obrazovke sú dve čísla - jedno v modrom a druhé v červenom poli. Na začiatku sú obe čísla rovnaké. Pri každom pípnutí sa obe čísla zväčšia - v modrom poli o 1 a v červenom o 3. V jednej chvíli sa na obrazovke objaví v modrom poli 49 a v červenom poli č
Na obrazovke sú dve čísla - jedno v modrom a druhé v červenom poli. Na začiatku sú obe čísla rovnaké. Pri každom pípnutí sa obe čísla zväčšia - v modrom poli o 1 a v červenom o 3. V jednej chvíli sa na obrazovke objaví v modrom poli 49 a v červenom poli č - Dvojciferného 7607
 Ciferný súčet dvojciferného čísla Je 11. Po zámene poradia číslic dostanem číslo, ktoré je o 27 menšie ako myslené číslo. Aké číslo si myslím?
Ciferný súčet dvojciferného čísla Je 11. Po zámene poradia číslic dostanem číslo, ktoré je o 27 menšie ako myslené číslo. Aké číslo si myslím? - Ušetrených 7606
 Jana a Dana majú dohromady ušetrených 220 korún. Jana utratila pätinu svojich úspor, Dana štvrtinu. Potom im dohromady zostalo 150 Kč. Koľko majú ušetrené?
Jana a Dana majú dohromady ušetrených 220 korún. Jana utratila pätinu svojich úspor, Dana štvrtinu. Potom im dohromady zostalo 150 Kč. Koľko majú ušetrené?
- Hĺbkový uhol
 Z útesu vysokého 150 metrov je vidieť na mori loď pod hĺbkovým uhlom 9°. Ako ďaleko je loď od útesu?
Z útesu vysokého 150 metrov je vidieť na mori loď pod hĺbkovým uhlom 9°. Ako ďaleko je loď od útesu? - Auto ide
 Auto ide z mesta A do mesta B priemernou rýchlosťou 70 km/h, naspäť priemernou rýchlosťou 50 km/h. Keby išlo tam aj späť priemernou rýchlosťou 60 km/h, celá jazda by trvala o 8 minút menej. Aká je vzdialenosť medzi mestami A a B?
Auto ide z mesta A do mesta B priemernou rýchlosťou 70 km/h, naspäť priemernou rýchlosťou 50 km/h. Keby išlo tam aj späť priemernou rýchlosťou 60 km/h, celá jazda by trvala o 8 minút menej. Aká je vzdialenosť medzi mestami A a B? - Kvapalina ohrev
 Bezfarebná kvapalina s hmotnosťou m = 200g, je za stáleho miešania zahrievaná na variči s príkonom P0 = 600W, na zahrievanie kvapaliny sa z dodanej energie využije 80%. Vybrané namerané hodnoty teploty kvapaliny v závislosti od času sú zaznamenané v tabuľ
Bezfarebná kvapalina s hmotnosťou m = 200g, je za stáleho miešania zahrievaná na variči s príkonom P0 = 600W, na zahrievanie kvapaliny sa z dodanej energie využije 80%. Vybrané namerané hodnoty teploty kvapaliny v závislosti od času sú zaznamenané v tabuľ - Dôchodok 2
 Akou sumou, vloženou začiatkom roka, sa zabezpečí ročný dôchodok vo výške 1000 eur, splatný vždy na konci daného roka a trvajúci 10 rokov, pričom vložená suma sa každoročne úročí úrokovou sadzbou 2 %
Akou sumou, vloženou začiatkom roka, sa zabezpečí ročný dôchodok vo výške 1000 eur, splatný vždy na konci daného roka a trvajúci 10 rokov, pričom vložená suma sa každoročne úročí úrokovou sadzbou 2 % - Súčet obsahov
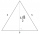 Nád výškou rovnostranného trojuholníka ABC je zostrojený rovnostranný trojuholník A1, B1, C1, nad jeho výškou je zostrojený rovnostranný trojuholník A2, B2, C2, atd. Sa postup neustale opakuje. Aký je veľký súčet obsahov všetkých trojuholníkov, ak strana
Nád výškou rovnostranného trojuholníka ABC je zostrojený rovnostranný trojuholník A1, B1, C1, nad jeho výškou je zostrojený rovnostranný trojuholník A2, B2, C2, atd. Sa postup neustale opakuje. Aký je veľký súčet obsahov všetkých trojuholníkov, ak strana
- Štvoruholníka 7583
 Pre veľkosti vnútorných uhlov štvoruholníka ABCD platí: uhol alfa je o 26° väčší ako uhol beta, dvojnásobok uhla Beta je o 5° menší ako uhol gama a uhol gama je o 36° väčší ako uhol delta. Určite uhly.
Pre veľkosti vnútorných uhlov štvoruholníka ABCD platí: uhol alfa je o 26° väčší ako uhol beta, dvojnásobok uhla Beta je o 5° menší ako uhol gama a uhol gama je o 36° väčší ako uhol delta. Určite uhly. - Polomer 10
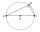 Polomer kružnice opísanej pravouhlému trojuholníku s odvesnou dlhou 6 cm, je 5 cm. Vypočítajte obvod tohto trojuholníka.
Polomer kružnice opísanej pravouhlému trojuholníku s odvesnou dlhou 6 cm, je 5 cm. Vypočítajte obvod tohto trojuholníka. - Osový rez
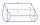 Vypočítajte objem a povrch valca, ktorého osový rez je obdĺžnik široký 15 cm s uhlopriečkou dlhou 25 cm.
Vypočítajte objem a povrch valca, ktorého osový rez je obdĺžnik široký 15 cm s uhlopriečkou dlhou 25 cm. - O ôsmej
 O ôsmej ráno sa vybral z mesta K do mesta L cyklista. V meste L sa zdržal 4,25 hodiny a vrátil sa domov o 15. Hodine. Vypočítajte vzdialenosť medzi mestami K a L, ak cyklista išiel do mesta L rýchlosťou 12 km/h a z mesta L do mesta K rýchlosťou 10 km/h.
O ôsmej ráno sa vybral z mesta K do mesta L cyklista. V meste L sa zdržal 4,25 hodiny a vrátil sa domov o 15. Hodine. Vypočítajte vzdialenosť medzi mestami K a L, ak cyklista išiel do mesta L rýchlosťou 12 km/h a z mesta L do mesta K rýchlosťou 10 km/h. - Do kruhu
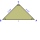 Do kruhu s r=8cm bol vpísaný pravouhlý rovnoramenny trojuholník. Zisti jeho S. Koľko % zaberá trojuholník z plochy kruhu?
Do kruhu s r=8cm bol vpísaný pravouhlý rovnoramenny trojuholník. Zisti jeho S. Koľko % zaberá trojuholník z plochy kruhu?
- Amfiteáter
 Amfiteáter má tvar polkruhu. Pódium je priemer polkruhu. Diváci K, L, M, N, O sedia po obvode. Kto vidí pódium pod najväčším uhlom?
Amfiteáter má tvar polkruhu. Pódium je priemer polkruhu. Diváci K, L, M, N, O sedia po obvode. Kto vidí pódium pod najväčším uhlom? - Piati
 Spoločnosť 5 ľudí má priemerný vek 46 rokov. Priemerný vek prvých štyroch z nich je 43 rokov. Piaty má. ..
Spoločnosť 5 ľudí má priemerný vek 46 rokov. Priemerný vek prvých štyroch z nich je 43 rokov. Piaty má. .. - V triede
 V triede je 32 žiakov, pričom dievčat je o dve tretiny viac ako chlapcov. a) O koľko percent viac je dievčat ako chlapcov? Výsledok zaokrúhlite na celé percenta. b) Koľko je v triede chlapcov? c) Určite v triede pomer chlapcov a dievčat v základnom tvare.
V triede je 32 žiakov, pričom dievčat je o dve tretiny viac ako chlapcov. a) O koľko percent viac je dievčat ako chlapcov? Výsledok zaokrúhlite na celé percenta. b) Koľko je v triede chlapcov? c) Určite v triede pomer chlapcov a dievčat v základnom tvare. - Firma
 V troch výrobných halách firmy pracuje 1116 osôb. V prvej z nich o 18% viac ako v tretej a zároveň o 60 osôb viac ako v druhej. Koľko zamestnancov pracuje v jednotlivých halách?
V troch výrobných halách firmy pracuje 1116 osôb. V prvej z nich o 18% viac ako v tretej a zároveň o 60 osôb viac ako v druhej. Koľko zamestnancov pracuje v jednotlivých halách? - Turista 14
 Turista prešiel v priebehu troch dní 47 km. Prvý deň prešiel o 20 percent viac ako druhý deň a tretí deň o 4 km menej ako druhý deň. Koľko km prešiel počas jednotlivých dní?
Turista prešiel v priebehu troch dní 47 km. Prvý deň prešiel o 20 percent viac ako druhý deň a tretí deň o 4 km menej ako druhý deň. Koľko km prešiel počas jednotlivých dní?
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
