Príklady pre stredoškolákov - strana 81 z 206
Počet nájdených príkladov: 4106
- Neznáme 13903
 Súčet dvoch celých čísel je 3 a ich rozdiel je 7. Urci neznáme čísla.
Súčet dvoch celých čísel je 3 a ich rozdiel je 7. Urci neznáme čísla. - Pravidelného 13891
 Vypočítaj prosím povrch pravidelného šesťbokového ihlanu s podstavou vpísanou do kružnice s polomerom 8cm a výškou 20cm. Načrtnite si obrázok prosím.
Vypočítaj prosím povrch pravidelného šesťbokového ihlanu s podstavou vpísanou do kružnice s polomerom 8cm a výškou 20cm. Načrtnite si obrázok prosím. - Štvorbokého 13881
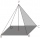 Vypočítaj prosím objem štvorbokého ihlana keď a=5cm a stenová výška má veľkosť w=12cm.
Vypočítaj prosím objem štvorbokého ihlana keď a=5cm a stenová výška má veľkosť w=12cm. - Dohromady 13871
 Po dvore behali psy a husi. Dohromady mali 12 hláv a 30 nôh. Koľko behalo po dvore husí a koľko psov?
Po dvore behali psy a husi. Dohromady mali 12 hláv a 30 nôh. Koľko behalo po dvore husí a koľko psov?
- Vendelína 13863
 Vendelín má 4/5 počtu pasteliek. Lenže keby si Maruška vzala z toho 1/2 zostalo by 20 pasteliek. Otázka znie, koľko pasteliek bolo ešte v penále pred odberom Vendelína
Vendelín má 4/5 počtu pasteliek. Lenže keby si Maruška vzala z toho 1/2 zostalo by 20 pasteliek. Otázka znie, koľko pasteliek bolo ešte v penále pred odberom Vendelína - Vypočítaj
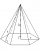 Vypočítaj prosím výšku pravidelného šesťbokého ihlanu s hranou podstavy 5cm a stenovou výškou w = 20cm. Načrtnite prosím obrázok.
Vypočítaj prosím výšku pravidelného šesťbokého ihlanu s hranou podstavy 5cm a stenovou výškou w = 20cm. Načrtnite prosím obrázok. - Veterníkov 13751
 Mamička kúpila na oslavu narodenín zakusky. Veterník stál 14 Sk, indianiek 11 Sk. Za 15 zákuskov zaplatila 201 Korún. Koľko kúpila veterníkov a koľko indiánov?
Mamička kúpila na oslavu narodenín zakusky. Veterník stál 14 Sk, indianiek 11 Sk. Za 15 zákuskov zaplatila 201 Korún. Koľko kúpila veterníkov a koľko indiánov? - Promile z percenta
 Vypočítaj 1,5 ‰ z 85% z 240
Vypočítaj 1,5 ‰ z 85% z 240 - Priemerom 13601
 Písmeno H je súčasťou štvorca ktorému je opísaná kružnica s priemerom 42 cm. Stačí na výrobu tohto písmena látka dĺžky 1 meter? Zanedbaj hrúbku látky.
Písmeno H je súčasťou štvorca ktorému je opísaná kružnica s priemerom 42 cm. Stačí na výrobu tohto písmena látka dĺžky 1 meter? Zanedbaj hrúbku látky.
- Tri oblúky
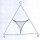 V rovnostrannom trojuholníku o strane 2cm sú zakreslené oblúky troch kružníc so stredmi vo vrcholoch trojuholníka a polomery 1cm. Vypočítaj obsah vyšrafovanej časti - útvaru ktory tvori rozdiel medzi plochou trojuholníka a kruhovými výšok.
V rovnostrannom trojuholníku o strane 2cm sú zakreslené oblúky troch kružníc so stredmi vo vrcholoch trojuholníka a polomery 1cm. Vypočítaj obsah vyšrafovanej časti - útvaru ktory tvori rozdiel medzi plochou trojuholníka a kruhovými výšok. - Trojuholníka 13541
 Uhol alfa je dvakrát väčší ako uhol beta a uhol gama je trikrát väčší ako uhol beta. Určite veľkosti všetkých vnútorných uhlov alfa, beta, gama trojuholníka ABC.
Uhol alfa je dvakrát väčší ako uhol beta a uhol gama je trikrát väčší ako uhol beta. Určite veľkosti všetkých vnútorných uhlov alfa, beta, gama trojuholníka ABC. - Cirkus
 Príchod cirkusu do Plzne zaznamenal ráno o 08:00 jeden občan mesta a túto informáciu odovzdal 08:15 ďalším trom obyvateľom mesta. Každý z týchto troch ľudí potom o 08:30 informoval ďalších troch obyvateľov, títo potom opäť v 08:45 odovzdali zvesť o prícho
Príchod cirkusu do Plzne zaznamenal ráno o 08:00 jeden občan mesta a túto informáciu odovzdal 08:15 ďalším trom obyvateľom mesta. Každý z týchto troch ľudí potom o 08:30 informoval ďalších troch obyvateľov, títo potom opäť v 08:45 odovzdali zvesť o prícho - Spoločnosťami 13451
 V tabuľke nižšie sú uvedené ceny akcií, zisk na akciu a dividendy na akciu pre tri spoločnosti za posledný rok: Deere & Co. Cena 65,70 USD zisk na akciu 4,40 USD Dividendy na akciu 1,16 USD Cena Google 528,33 USD zisk na akciu 27,72 USD Dividendy na akciu
V tabuľke nižšie sú uvedené ceny akcií, zisk na akciu a dividendy na akciu pre tri spoločnosti za posledný rok: Deere & Co. Cena 65,70 USD zisk na akciu 4,40 USD Dividendy na akciu 1,16 USD Cena Google 528,33 USD zisk na akciu 27,72 USD Dividendy na akciu - Vypočítajte 17
 Vypočítajte povrch pravidelného šesťbokého hranola, ktorého podstavná hrana a = 12cm a bočná hrana b = 3 dm.
Vypočítajte povrch pravidelného šesťbokého hranola, ktorého podstavná hrana a = 12cm a bočná hrana b = 3 dm.
- Družstvo 2
 Družstvo zožalo 390 ton obilia. Pšenice bolo o 15% viac ako jačmeňa, raže bolo o 126 ton menej ako pšenice a jačmena dohromady. Kolko ton pšenice, kolko ton jačmena a kolko raže družstvo zožalo?
Družstvo zožalo 390 ton obilia. Pšenice bolo o 15% viac ako jačmeňa, raže bolo o 126 ton menej ako pšenice a jačmena dohromady. Kolko ton pšenice, kolko ton jačmena a kolko raže družstvo zožalo? - Trend úbytku
 V Plzenskom kraji medzi rokmi 2000 a 2001 ubudlo 14 promile obyvateľov. V roku 2000 mal Plzensky kraj 551281 obyvateľov. Keby trend úbytku pokračoval stále rovnako (každý rok teda ubúdalo 14 promile obyvateľov), koľko obyvateľov bude mať Plzeňský kraj v r
V Plzenskom kraji medzi rokmi 2000 a 2001 ubudlo 14 promile obyvateľov. V roku 2000 mal Plzensky kraj 551281 obyvateľov. Keby trend úbytku pokračoval stále rovnako (každý rok teda ubúdalo 14 promile obyvateľov), koľko obyvateľov bude mať Plzeňský kraj v r - Vozík
 Chlapec tlačí vozík silou F1 = 20N. Vozík pôsobí na chlapca silou F2. Aká veľká je táto sila?
Chlapec tlačí vozík silou F1 = 20N. Vozík pôsobí na chlapca silou F2. Aká veľká je táto sila? - Ciferný súčet
 Ciferný súčet dvojciferný prirodzeného čísla je 11. Keď v ňom zameníme poradí číslic, dostanem číslo, ktoré je o 27 menej ako myslenej číslo. Zisti, ktoré číslo si myslím.
Ciferný súčet dvojciferný prirodzeného čísla je 11. Keď v ňom zameníme poradí číslic, dostanem číslo, ktoré je o 27 menej ako myslenej číslo. Zisti, ktoré číslo si myslím. - Korálky
 Koľkými spôsobmi môžeme navliecť na niť 4 červené, 5 modrých a 6 žltých korálok?
Koľkými spôsobmi môžeme navliecť na niť 4 červené, 5 modrých a 6 žltých korálok?
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
