Päťuholník
Vo vnútri pravidelného päťuholníka ABCDE je bod P taký, že trojuholník ABP je rovnostranný. Aký veľký je uhol BCP?
Urob si náčrtok.
Urob si náčrtok.
Správna odpoveď:
Zobrazujem 1 komentár:
Mo - Ofic
Nápoveda. Uvedomte si, že trojuholník BCP nie je obyčajný.
Možné riešenie. Päťuholník ABCDE je pravidelný, najmä platí | AB | = | BC |. Trojuholník ABP je rovnostranný, najmä platí | AB | = | BP |. Odtiaľ vidíme, že | BP | = | BC |, teda, že trojuholník BCP je rovnoramenný. Jeho vnútorné uhly pri vrcholoch P a C sú preto zhodné; na ich určenie stačí poznať uhol pri vrchole B (súčet veľkostí vnútorných uhlov v ľubovoľnom trojuholníku je 180◦). Pritom uhol P BC je rozdielom uhlov ABC a ABP, z ktorých prvá je vnútorným uhlom pravidelného päťuholníka (vyjadríme vzápätí) a druhý je vnútorným uhlom rovnostranného trojuholníka (má veľkosť α = 60◦).
Päťuholník ABCDE môžeme rozdeliť na päť trojuholníkov so spoločným vrcholom P. Súčet vnútorných uhlov päťuholníka je rovný súčtu vnútorných uhlov všetkých piatich trojuholníkov výnimkou uhlov pri vrchole P, tj. 5 · 180◦-360◦ = 540◦. V pravidelnom päťuholníka sú všetky vnútorné uhly zhodné, každý má teda veľkosť 540◦: 5 = 108◦.
Odtiaľ konečne vieme vyjadriť β = |uhol PBC | = |uhol ABC | - |uhol ABP | = 108◦ - 60◦ = 48◦ a následne γ = |uhol BCP | = |uhol BPC | = (180◦ - 48◦) / 2 = 66◦.
Veľkosť uhla BCP je 66◦.
Poznámka. Veľkosť vnútorného uhla pravidelného päťuholníka je možné odvodiť aj pomocou rozdelenia na päť zhodných rovnoramenných trojuholníkov ako na nasledujúcom obrázku (S je stred päťuholníka, tj. Stred jemu opísanej kružnice).
Uhol pri vrchole S v každom z týchto trojuholníkov má veľkosť 360: 5 = 72◦; súčet uhlov pri základni je rovný 180◦-72◦ = 108◦, čo je tiež veľkosť vnútorného uhla pravidelného päťuholníka.
Možné riešenie. Päťuholník ABCDE je pravidelný, najmä platí | AB | = | BC |. Trojuholník ABP je rovnostranný, najmä platí | AB | = | BP |. Odtiaľ vidíme, že | BP | = | BC |, teda, že trojuholník BCP je rovnoramenný. Jeho vnútorné uhly pri vrcholoch P a C sú preto zhodné; na ich určenie stačí poznať uhol pri vrchole B (súčet veľkostí vnútorných uhlov v ľubovoľnom trojuholníku je 180◦). Pritom uhol P BC je rozdielom uhlov ABC a ABP, z ktorých prvá je vnútorným uhlom pravidelného päťuholníka (vyjadríme vzápätí) a druhý je vnútorným uhlom rovnostranného trojuholníka (má veľkosť α = 60◦).
Päťuholník ABCDE môžeme rozdeliť na päť trojuholníkov so spoločným vrcholom P. Súčet vnútorných uhlov päťuholníka je rovný súčtu vnútorných uhlov všetkých piatich trojuholníkov výnimkou uhlov pri vrchole P, tj. 5 · 180◦-360◦ = 540◦. V pravidelnom päťuholníka sú všetky vnútorné uhly zhodné, každý má teda veľkosť 540◦: 5 = 108◦.
Odtiaľ konečne vieme vyjadriť β = |uhol PBC | = |uhol ABC | - |uhol ABP | = 108◦ - 60◦ = 48◦ a následne γ = |uhol BCP | = |uhol BPC | = (180◦ - 48◦) / 2 = 66◦.
Veľkosť uhla BCP je 66◦.
Poznámka. Veľkosť vnútorného uhla pravidelného päťuholníka je možné odvodiť aj pomocou rozdelenia na päť zhodných rovnoramenných trojuholníkov ako na nasledujúcom obrázku (S je stred päťuholníka, tj. Stred jemu opísanej kružnice).
Uhol pri vrchole S v každom z týchto trojuholníkov má veľkosť 360: 5 = 72◦; súčet uhlov pri základni je rovný 180◦-72◦ = 108◦, čo je tiež veľkosť vnútorného uhla pravidelného päťuholníka.
8 rokov 1 Like
Tipy na súvisiace online kalkulačky
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Špeh a opilec
 Po dlhom večeri vo vnútri salónika v tvare štvorca ABCD leží opitý kupec E tak, že trojuholník DEC je rovnostranný. Na hrane BC leží špeh F, pričom |EB|=|EF|. Aká je veľkosť uhla CEF?
Po dlhom večeri vo vnútri salónika v tvare štvorca ABCD leží opitý kupec E tak, že trojuholník DEC je rovnostranný. Na hrane BC leží špeh F, pričom |EB|=|EF|. Aká je veľkosť uhla CEF? - Obdĺžnikový 36111
 Vypočítaj, ak sa zmestí obdĺžnikový obraz s rozmermi 33cm a 70cm do kufra s rozmermi 65cm, 40cm a 20cm. Urob si náčrtok, zapíš ako slovnú úlohu.
Vypočítaj, ak sa zmestí obdĺžnikový obraz s rozmermi 33cm a 70cm do kufra s rozmermi 65cm, 40cm a 20cm. Urob si náčrtok, zapíš ako slovnú úlohu. - Päťuholník 6
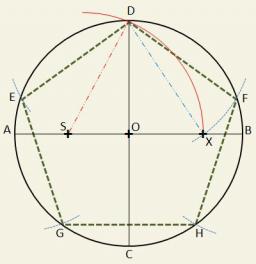
 Vývesný štít má tvar päťuholníka ABCDE, v ktorom úsečka BC je kolmá na úsečku AB a EA je kolmá na úsečku AB. Bod P je päta kolmice spustenie z bodu D na úsečku AB. |AP|=|PB|, |BC|=|EA|=6dm, |PD|=8,4dm. Na štíte je vyznačený bod X - priesečník úsečiek PE a
Vývesný štít má tvar päťuholníka ABCDE, v ktorom úsečka BC je kolmá na úsečku AB a EA je kolmá na úsečku AB. Bod P je päta kolmice spustenie z bodu D na úsečku AB. |AP|=|PB|, |BC|=|EA|=6dm, |PD|=8,4dm. Na štíte je vyznačený bod X - priesečník úsečiek PE a - Rovnoramenný lichobežník 2
 Daný je rovnoramenný lichobežník ABCD, v ktorom platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho strane BC je bod K taký, že |BK| = 2|KC|, na jeho strane CD je bod L taký, že |CL|= 2|LD|, a na jeho strane DA je bod M taký, že|DM|= 2|MA|. Určte veľkosti vnútorných
Daný je rovnoramenný lichobežník ABCD, v ktorom platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho strane BC je bod K taký, že |BK| = 2|KC|, na jeho strane CD je bod L taký, že |CL|= 2|LD|, a na jeho strane DA je bod M taký, že|DM|= 2|MA|. Určte veľkosti vnútorných - Päťuholník
 Vypočítajte obsah pravidelného päťuholníka, ktorého uhlopriečka je dlhá u=15.
Vypočítajte obsah pravidelného päťuholníka, ktorého uhlopriečka je dlhá u=15. - Obdĺžnik vs päťuholník
 Obdĺžnik má dĺžky stran |JA|=16cm a |AN|=12cm. Bod S je stred strany JO a bod T je stred strany JA. Vypočítajte obvod päťuholníka v cm.
Obdĺžnik má dĺžky stran |JA|=16cm a |AN|=12cm. Bod S je stred strany JO a bod T je stred strany JA. Vypočítajte obvod päťuholníka v cm. - Obsah päťuholníka
 Vypočítajte obsah pravidelného päťuholníka so stranou 31 cm.
Vypočítajte obsah pravidelného päťuholníka so stranou 31 cm. - Uhlopriečky päťuholníka
 Vypočítajte dĺžku uhlopriečky pravidelného päťuholníka: a) vpísaného do kružnice s polomerom 12 dm; b) opísaného kruhu s polomerom 12 dm.
Vypočítajte dĺžku uhlopriečky pravidelného päťuholníka: a) vpísaného do kružnice s polomerom 12 dm; b) opísaného kruhu s polomerom 12 dm. - Rovnostranný 14873
 Je daná kružnica s polomerom 2,5 cm a bod A, ktorý na ňu leží. Do kružnice vpíšte rovnostranný trojuholník ABC.
Je daná kružnica s polomerom 2,5 cm a bod A, ktorý na ňu leží. Do kružnice vpíšte rovnostranný trojuholník ABC. - Päťuholník
 Vypočítajte dĺžku strany a, obvod a obsah pravidelného päťuholníka, ktorý je vpísaný do kružnice s polomerom r = 6 cm.
Vypočítajte dĺžku strany a, obvod a obsah pravidelného päťuholníka, ktorý je vpísaný do kružnice s polomerom r = 6 cm. - Obdĺžnik
 V obdĺžniku so stranami 6 a 3 vyznačíme uhlopriečku. Aká je pravdepodobnosť, že náhodne zvolený bod vnútri obdĺžnika je bližšie k tejto uhlopriečke, ako k ľubovoľnej strane obdĺžnika?
V obdĺžniku so stranami 6 a 3 vyznačíme uhlopriečku. Aká je pravdepodobnosť, že náhodne zvolený bod vnútri obdĺžnika je bližšie k tejto uhlopriečke, ako k ľubovoľnej strane obdĺžnika? - Body ABC
 Body ABC ležia na kružnici k(S, r) tak, že uhol pri B je tupý. Aký veľký musí byť uhol pri vrchole B štvoruholníka SCBA, aby bol tento uhol trikrát väčší ako vnútorný uhol ASC toho istého štvoruholníka?
Body ABC ležia na kružnici k(S, r) tak, že uhol pri B je tupý. Aký veľký musí byť uhol pri vrchole B štvoruholníka SCBA, aby bol tento uhol trikrát väčší ako vnútorný uhol ASC toho istého štvoruholníka? - Rovnostranný 3uholník
 Rovnostranný trojuholník má obvod 36 dm. Aký má obsah?
Rovnostranný trojuholník má obvod 36 dm. Aký má obsah? - Priesečnicu 5277
 Je daný pravidelný štvorboký ihlan ABCDV, vo vnútri jeho hrany AV je bod M, na preslúženej úsečke DC za bod C je bod N. Zostrojte priesečnicu roviny MNV s rovinou BCV a priesečník priamky MN a roviny BCV.
Je daný pravidelný štvorboký ihlan ABCDV, vo vnútri jeho hrany AV je bod M, na preslúženej úsečke DC za bod C je bod N. Zostrojte priesečnicu roviny MNV s rovinou BCV a priesečník priamky MN a roviny BCV. - Rovná 4
 Rovná cesta má stúpanie 19%. Aký veľký je uhol stúpania?
Rovná cesta má stúpanie 19%. Aký veľký je uhol stúpania? - Súčet obsahov
 Nád výškou rovnostranného trojuholníka ABC je zostrojený rovnostranný trojuholník A1, B1, C1, nad jeho výškou je zostrojený rovnostranný trojuholník A2, B2, C2, atd. Sa postup neustale opakuje. Aký je veľký súčet obsahov všetkých trojuholníkov, ak strana
Nád výškou rovnostranného trojuholníka ABC je zostrojený rovnostranný trojuholník A1, B1, C1, nad jeho výškou je zostrojený rovnostranný trojuholník A2, B2, C2, atd. Sa postup neustale opakuje. Aký je veľký súčet obsahov všetkých trojuholníkov, ak strana - Tetiva
 Bod na kružnici je krajným bodom priemeru a tetivy veľkosti polomeru. Aký uhol zviera priemer s tetivou?
Bod na kružnici je krajným bodom priemeru a tetivy veľkosti polomeru. Aký uhol zviera priemer s tetivou?
