Volebná matematika
Vo voľbách získalo 14 politických strán takéto podiely hlasov voličov:
party A 49,8 %
party B 11,4 %
party C 7,9 %
party D 6,3 %
party E 6,1 %
party F 5,7 %
party G 4,6 %
party H 2,9 %
party I 2,2 %
party J 1,3 %
party K 1 %
party L 0,7 %
party M 0,1 %
Vypočítajte aké podiely získajú v parlamente, ak minimálne kvórum na postup do parlamentu je 5%.
party A 49,8 %
party B 11,4 %
party C 7,9 %
party D 6,3 %
party E 6,1 %
party F 5,7 %
party G 4,6 %
party H 2,9 %
party I 2,2 %
party J 1,3 %
party K 1 %
party L 0,7 %
party M 0,1 %
Vypočítajte aké podiely získajú v parlamente, ak minimálne kvórum na postup do parlamentu je 5%.
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Potrebujete pomôcť spočítať, vykrátiť či vynásobiť zlomky? Skúste našu zlomkovú kalkulačku.
Naša kalkulačka na výpočet percent Vám pomôže rýchlo vypočítať rôzne typické úlohy s percentami.
Vyskúšajte našu kalkulačka na prepočet pomeru.
Naša kalkulačka na výpočet percent Vám pomôže rýchlo vypočítať rôzne typické úlohy s percentami.
Vyskúšajte našu kalkulačka na prepočet pomeru.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Zrýchlenie 9
 Zrýchlenie hmotného bodu pri jeho priamočiarom pohybe rovnomerne klesá zo začiatočnej hodnoty a0 = 10 m/s² v čase t0 = 0 na nulovú hodnotu počas 20 s. Aká je rýchlosť hmotného bodu v čase t1 = 20 s a akú dráhu za ten čas hmotný bod prešiel, keď v čase t0
Zrýchlenie hmotného bodu pri jeho priamočiarom pohybe rovnomerne klesá zo začiatočnej hodnoty a0 = 10 m/s² v čase t0 = 0 na nulovú hodnotu počas 20 s. Aká je rýchlosť hmotného bodu v čase t1 = 20 s a akú dráhu za ten čas hmotný bod prešiel, keď v čase t0 - Inverzná 3
 Inverzná funkcia k funkcii f(x) = √(x-3) pre x ≥ 3 je funkcia:
Inverzná funkcia k funkcii f(x) = √(x-3) pre x ≥ 3 je funkcia: - Vypočítaj 435
 Vypočítaj hodnotu výrazu V = 3x²- 2x + 3 pre x = -2.
Vypočítaj hodnotu výrazu V = 3x²- 2x + 3 pre x = -2. - -2x-4y-20=0 82677
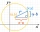 Určite súradnice vrcholu obdĺžnika vpísaného do kružnice x²+y² -2x-4y-20=0, ak viete, že jedna jeho strana leží na priamke p: x+2y=0
Určite súradnice vrcholu obdĺžnika vpísaného do kružnice x²+y² -2x-4y-20=0, ak viete, že jedna jeho strana leží na priamke p: x+2y=0 - Napíšte 8
 Napíšte rovnicu dotyčnice hyperboly 9x²−4y²=36 v bode T =[t1,4].
Napíšte rovnicu dotyčnice hyperboly 9x²−4y²=36 v bode T =[t1,4]. - Napíšte 7
 Napíšte rovnicu elipsy, ktorá prechádzada bodmi a jej osi sú totožné so súradnicovými osami, ked’: A = [2, 3] a B = [−1, −4].
Napíšte rovnicu elipsy, ktorá prechádzada bodmi a jej osi sú totožné so súradnicovými osami, ked’: A = [2, 3] a B = [−1, −4]. - Určte 19
 Určte rovnicu kružnice, ktorá je množinou všetkých bodov roviny, ktoré majú od bodu [3,7] dvakrát väčšiu vzdialenosť ako od bodu [0,1].
Určte rovnicu kružnice, ktorá je množinou všetkých bodov roviny, ktoré majú od bodu [3,7] dvakrát väčšiu vzdialenosť ako od bodu [0,1]. - Spotreba
 Spotreba benzínu na kilometer M (jednotka kilometer na liter) auta Dodge Caliber je modelovaná funkciou M(s) = - 1/28s² + 3s- 31 Akú má auto najlepšiu spotrebu (benzínové kilometre) a akú rýchlosť dosiahne?
Spotreba benzínu na kilometer M (jednotka kilometer na liter) auta Dodge Caliber je modelovaná funkciou M(s) = - 1/28s² + 3s- 31 Akú má auto najlepšiu spotrebu (benzínové kilometre) a akú rýchlosť dosiahne? - Vypočítaj 391
 Vypočítaj x v úmerach: x:7=6:4 1/2:x=5:3/4 4:3=8:x
Vypočítaj x v úmerach: x:7=6:4 1/2:x=5:3/4 4:3=8:x - Funkce parabolická
 Je dána funkce y = x² - 4x + 3 Určete všechna reálná čísla z tak, aby platilo g(x) = g(-2).
Je dána funkce y = x² - 4x + 3 Určete všechna reálná čísla z tak, aby platilo g(x) = g(-2). - Proporcionálny 74524
 Ktorá tabuľka ukazuje proporcionálny vzťah medzi x a y? A) x 3 9 10 15 y 1 3 4 5 B) x 2 3 5 6 y 3 4 7 9 c) x 1 5 8 10 r 15 75 120 150 D) x 4 6 8 10 y 6 8 10 12
Ktorá tabuľka ukazuje proporcionálny vzťah medzi x a y? A) x 3 9 10 15 y 1 3 4 5 B) x 2 3 5 6 y 3 4 7 9 c) x 1 5 8 10 r 15 75 120 150 D) x 4 6 8 10 y 6 8 10 12 - Ruské
 Ruské koleso s priemerom 100 stôp vykoná 5 otáčok každých 8 minút. Základňa kolesa je 4 stopy nad zemou. Váš priateľ začína presne o 15:00. a) napíšte rovnicu na vyjadrenie výšky vášho priateľa v stopách v ľubovoľnom čase v sekundách. b) aká je výška tvoj
Ruské koleso s priemerom 100 stôp vykoná 5 otáčok každých 8 minút. Základňa kolesa je 4 stopy nad zemou. Váš priateľ začína presne o 15:00. a) napíšte rovnicu na vyjadrenie výšky vášho priateľa v stopách v ľubovoľnom čase v sekundách. b) aká je výška tvoj - V škole 10
 V škole je p prvákov. Druhákov je o 18% menej ako prvákov. Tretiakov je o 7 viac ako druhákov a štvrtákov je dvakrát toľko ako prvákov a druhákov spolu. Vyjadri počet žiakov na 1. stupni.
V škole je p prvákov. Druhákov je o 18% menej ako prvákov. Tretiakov je o 7 viac ako druhákov a štvrtákov je dvakrát toľko ako prvákov a druhákov spolu. Vyjadri počet žiakov na 1. stupni. - Priesečníky 62534
 Rovnica linearnou funkciou je : y=-3x+4 a) urči priesečníky s osami načrtni graf b) pre ktoré x platí f(x)=-1 c) pre ktoré x platí f(x)=0 d) pre ktoré y platí f(-1/2)=y
Rovnica linearnou funkciou je : y=-3x+4 a) urči priesečníky s osami načrtni graf b) pre ktoré x platí f(x)=-1 c) pre ktoré x platí f(x)=0 d) pre ktoré y platí f(-1/2)=y - Odhadnite odmocninu
 Odhadnite √38 s presnosťou na stotiny pomocou ktorejkoľvek z dvoch metód (metóda delenia a priemeru alebo vzorec na odhad druhej odmocniny).
Odhadnite √38 s presnosťou na stotiny pomocou ktorejkoľvek z dvoch metód (metóda delenia a priemeru alebo vzorec na odhad druhej odmocniny). - Vedecký experiment
 Počas vedeckého experimentu sa kvapalina zahrievala rýchlosťou 8 stupňov Celzia za minútu počas 10 minút. Potom sa nechalo stratiť teplo rýchlosťou 6 stupňov Celzia za minútu. Ak bola konečná teplota 76 stupňov Celzia, aká bola teplota pred 16 minútami?
Počas vedeckého experimentu sa kvapalina zahrievala rýchlosťou 8 stupňov Celzia za minútu počas 10 minút. Potom sa nechalo stratiť teplo rýchlosťou 6 stupňov Celzia za minútu. Ak bola konečná teplota 76 stupňov Celzia, aká bola teplota pred 16 minútami? - Rozviňte
 Rozviňte funkciu f(z) do Laurentovho radu v bode z0 pre dané medzikružie f(z)=1/((z-2)*(z-3)) a) z0=2, 03
Rozviňte funkciu f(z) do Laurentovho radu v bode z0 pre dané medzikružie f(z)=1/((z-2)*(z-3)) a) z0=2, 03
