Permutace bez opakování

Kalkulačka vypočítá počet permutací n prvků. Permutace n prvků je každá uspořádaná n-tice vytvořená z těchto prvků. Permutace bez opakování z prvků je variace n-té třídy z n prvků. Slovo permutovat znamená obměňovat.

Počet prvků:

(n)

Vypočítej

Trošku teorie - základy kombinatoriky

Permutace

Permutace je synonymický název pro variaci n-té třídy z n-prvků. Je to tedy každá n-prvková uspořádána skupina vytvořená z n-prvků. Prvky se neopakují a záleží na pořadí prvků ve skupině.

P(n)=n(n−1)(n−2)...1=n!

Typický příklad je: Máme 4 knihy a kolika způsoby jejich můžeme uspořádat vedle sebe v poličce?

Základy kombinatoriky v slovních úlohách

• Zasedací pořádek
  Kolika způsoby se může posadit 6 osob na 6 židlí (např. obstarávání lístků ve vlaku)?
• Obdélníky
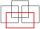  Kolik je obdélníků, jejichž délky stran jsou vyjádřeny přirozenými čísly a mají obsah 8937 cm²?
• 7 statečných
  9 hrdinů cválá na 9 koních za sebou. Kolika způsoby je lze seřadit za sebou?
• Manželé
  U stolu sedí 16 lidí, 8 na jedné a 8 na opačné straně. Mezi nimi jsou 7 manželské páry. Každý manželský pár chce sedět naproti sobě. Kolika způsoby se mohou usadit?
• Kopec
  Do kopce vedou 4 cesty a 1 lanovka. a) kolik je všech možností tam a zpět b) kolik je všech možností aby cesta tam a zpět nebyla stejná c) kolik je všech možností abychom šli alespoň jednou lanovkou

slovní úlohy - více »