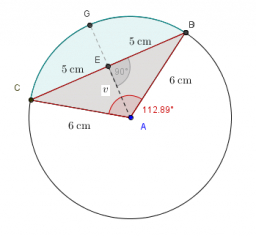
Calculate 65014
The radius of the circle is 5.5 cm. The height is 2.3 cm, which is the chord's distance. How can we calculate the length of the string?
Final Answer:
Tips for related online calculators
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Two chords
In a circle with a radius of 8.5 cm, two parallel chords are constructed, the lengths of which are 9 cm and 12 cm. Find the distance of the chords in a circle. - Two chords 6
A chord PQ is 10.4cm long, and its distance from the center of a circle is 3.7cm. Calculate the length of a second chord RS, which is 4.1cm from the center of this circle. - Two chords 2 The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm away from the center of the circle, calculate the length of the second chord.
- Determine 6415
Determine the distance of two parallel chords of lengths of 7 cm and 11 cm in a circle with a radius of 7 cm. - Circles
In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both). - Two parallel chords
The two parallel chords of the circle have the same length of 6 cm and are 8 cm apart. Calculate the radius of the circle. - Two chords
There is a given circle k (center S, radius r). From point A, which lies on circle k, are starting two chords of length r. What angle do chords make? Draw and measure.
