Quadratic Equation Calculator

A quadratic equation has the basic form:

a x^{2} + b x + c = 0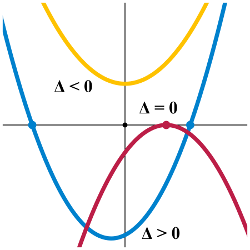

Enter the coefficients a, b, and c of the quadratic equation in its basic standardized form. The solution of a quadratic equation usually consists of two distinct real or complex roots, or one double root — calculated using the discriminant.

Calculation:

Solution in text:

1.5707963267949D²+15.707963267949D-112=0 ... quadratic equation

Discriminant:
D = b² - 4ac = 950.4568644313
D > 0 ... The equation has two distinct real roots

D₁ = 4.8133284
D₂ = -14.8133284

P = {4.8133284; -14.8133284}