Length - practice problems - page 3 of 163
Number of problems found: 3249
- Two trains 13
 Two trains start at the same time toward each other from stations A and B at respective speeds of 36 km/h and 42 km/h. When they meet, it was found that one train has covered 48 km more than the other. Find the distance between the two stations.
Two trains start at the same time toward each other from stations A and B at respective speeds of 36 km/h and 42 km/h. When they meet, it was found that one train has covered 48 km more than the other. Find the distance between the two stations. - The vertices
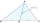 The vertices of a triangle are A (-1,3), B (1,-1), and C (5, 1). Find the length of the median through the vertex C.
The vertices of a triangle are A (-1,3), B (1,-1), and C (5, 1). Find the length of the median through the vertex C. - Speed Adjustment
 By increasing the speed of his car by 15 km/h, a person covers a 300 km distance in an hour less than before. What was the original speed?
By increasing the speed of his car by 15 km/h, a person covers a 300 km distance in an hour less than before. What was the original speed? - RT with rectangle
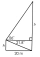 In the diagram, find the lengths h and b. One rectangle and one right triangle share one side. We know two angles and the length of the common side, as shown in the picture.
In the diagram, find the lengths h and b. One rectangle and one right triangle share one side. We know two angles and the length of the common side, as shown in the picture. - A bike 2
 A bike is running 72 km/hr. How much distance will it cover in 15 seconds?
A bike is running 72 km/hr. How much distance will it cover in 15 seconds? - Selling cloth
 By selling 33 m of cloth, a shopkeeper loses an amount equal to the selling price of 3 m of cloth. Find his gain or loss percentage.
By selling 33 m of cloth, a shopkeeper loses an amount equal to the selling price of 3 m of cloth. Find his gain or loss percentage. - A capsule
 A medicine capsule is a cylinder with two hemispheres stuck to each end. Its length is 14 mm, and its diameter is 5 mm. Find its surface area.
A medicine capsule is a cylinder with two hemispheres stuck to each end. Its length is 14 mm, and its diameter is 5 mm. Find its surface area. - Jeremy 2
 Jeremy is digitally editing out some red-eye problems in the photos from his sister's birthday party. The eyes are small and hard to click on, so he zooms in on the photo from 100% to 400%. In the zoomed-in photo, the eyes are 3 cm wide. How many cm wide
Jeremy is digitally editing out some red-eye problems in the photos from his sister's birthday party. The eyes are small and hard to click on, so he zooms in on the photo from 100% to 400%. In the zoomed-in photo, the eyes are 3 cm wide. How many cm wide - An iron rod
 If 22.5 meters of a uniform iron rod weighs 85.5 kg, what will the length of 22.8 kilograms of the same rod?
If 22.5 meters of a uniform iron rod weighs 85.5 kg, what will the length of 22.8 kilograms of the same rod? - A train 4
 A train passes two bridges of 400 m and 260 m in 25 sec and 18 sec, respectively. Find the length and speed of the train.
A train passes two bridges of 400 m and 260 m in 25 sec and 18 sec, respectively. Find the length and speed of the train. - A boat 4
 A boat travels 25 km upstream in 5 hours and 25 km downstream in 2.5 hours. If the boat increased its speed by 3 km/h, it would take 1 hour less to travel the downstream distance. Find the speed of the stream.
A boat travels 25 km upstream in 5 hours and 25 km downstream in 2.5 hours. If the boat increased its speed by 3 km/h, it would take 1 hour less to travel the downstream distance. Find the speed of the stream. - Two points
 M and N are two points on the X-axis and Y-axis, respectively. Point P (3, 2) divides the line segment MN in a ratio of 2:3. Find: (i) the coordinates of M and N (ii) slope of the line MN.
M and N are two points on the X-axis and Y-axis, respectively. Point P (3, 2) divides the line segment MN in a ratio of 2:3. Find: (i) the coordinates of M and N (ii) slope of the line MN. - Elevation angle
 A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t
A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t - A boat 3
 A boat takes 1 hour longer to go 36 km up a river than to return. If the river flows at 3 km/h, find the rate at which the boat travels in still water.
A boat takes 1 hour longer to go 36 km up a river than to return. If the river flows at 3 km/h, find the rate at which the boat travels in still water. - Automobil
 The car traveled three quarters of the total journey at a speed of 90 km/h and the remaining part of the journey at a speed of 50 km/h. Find its average speed.
The car traveled three quarters of the total journey at a speed of 90 km/h and the remaining part of the journey at a speed of 50 km/h. Find its average speed. - The world record
 The world record for the longest dogtail is 77/100 meters. The previous record was 1/20 meter shorter than the current record. Was the previous record holder longer than 3/4 meter?
The world record for the longest dogtail is 77/100 meters. The previous record was 1/20 meter shorter than the current record. Was the previous record holder longer than 3/4 meter? - The dimensions
 The dimensions of a rectangular piece of paper are 22 cm × 14 cm. It is rolled once across the breadth and once across the length to form right circular cylinders of biggest possible surface area. Find the difference in volumes of the two cylinders that w
The dimensions of a rectangular piece of paper are 22 cm × 14 cm. It is rolled once across the breadth and once across the length to form right circular cylinders of biggest possible surface area. Find the difference in volumes of the two cylinders that w - A carpenter 3
 A carpenter bought a piece of wood that was 0.9 meters long. Then she sawed 0.8 meters off the end. How long is the piece of wood now?
A carpenter bought a piece of wood that was 0.9 meters long. Then she sawed 0.8 meters off the end. How long is the piece of wood now? - The distance 4
 The distance between two towns is 120 km there are approximately 8 km in each 5 mi. Which measurement is closest to the number of miles between each two towns?
The distance between two towns is 120 km there are approximately 8 km in each 5 mi. Which measurement is closest to the number of miles between each two towns? - Two trains 12
 Two trains 128m and 132m long are running towards each other on parallel lines at 42km/h and 30km/h respectively. In what time will they clear of each other from the moment they meet?
Two trains 128m and 132m long are running towards each other on parallel lines at 42km/h and 30km/h respectively. In what time will they clear of each other from the moment they meet?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
