Angle + unit conversion - practice problems
Number of problems found: 273
- A radio antenna
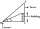 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - Three 235
 Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B.
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B. - Conjugate coordinates
 If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y.
If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y. - Subtract polar forms
 Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form - A lighthouse
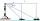 A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - Piece of a wire
 A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is
A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is - A boy 5
 A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A. - A triangle 7
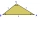 A triangle lot has the dimensions a=15m, b=10m, and c=20m. What is the measure of the angle between the sides of b and c?
A triangle lot has the dimensions a=15m, b=10m, and c=20m. What is the measure of the angle between the sides of b and c? - Using 4
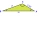 Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15.
Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15. - One side 4
 One side of a regular octagon is 12 inches. Find the apothem and its area.
One side of a regular octagon is 12 inches. Find the apothem and its area. - X-triangle
 Find the length of the x segment in the given triangle drawings.
Find the length of the x segment in the given triangle drawings. - The apothem
 The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area. - Electrics - conductor
 The wire is 107 meters long at 0 °C, and at every temperature increase of 1 °C, the length increases by 0.15 mm per 1 m length of wire. Determine a function that represents the wire's overall length as a temperature function. What is the length of the wir
The wire is 107 meters long at 0 °C, and at every temperature increase of 1 °C, the length increases by 0.15 mm per 1 m length of wire. Determine a function that represents the wire's overall length as a temperature function. What is the length of the wir - Beer
 After three 10° beers consumed in a short time, there is 5.6 g of alcohol in 6 kg adult human blood. How much is it per mille?
After three 10° beers consumed in a short time, there is 5.6 g of alcohol in 6 kg adult human blood. How much is it per mille? - Trigonometry
 If you know that cos(γ) = sin (806°), what is the angle γ?
If you know that cos(γ) = sin (806°), what is the angle γ? - Beer permille
 In the 5 kg of the blood of an adult human after three 10° beers consumed in a short time is 6.6 g of alcohol. How much is it per mille?
In the 5 kg of the blood of an adult human after three 10° beers consumed in a short time is 6.6 g of alcohol. How much is it per mille? - Which 9
 Which of the temperatures is the coldest? A.100 degrees Celsius, B.373 degree Kelvin, C. 32 degrees Fahrenheit.
Which of the temperatures is the coldest? A.100 degrees Celsius, B.373 degree Kelvin, C. 32 degrees Fahrenheit. - Lunch
 Lunch is given to seniors from 12:15 to 12:40 during the Coronavirus pandemic. What angle will the minute hand of the clock describe during this time?
Lunch is given to seniors from 12:15 to 12:40 during the Coronavirus pandemic. What angle will the minute hand of the clock describe during this time? - Time clock
 What are the angle of the hour hand and the minute hand if it is 0:40?
What are the angle of the hour hand and the minute hand if it is 0:40? - A straight angle
 A straight angle measures s, so you can subtract or add 85 from. What is the measure of their angles?
A straight angle measures s, so you can subtract or add 85 from. What is the measure of their angles?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
